题目

数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第5位（从下标0开始计数）是5，第13位是1，第19位是4，等等。

请写一个函数，求任意第n位对应的数字。

思路

我们注意到，如果：

将 01234567891⋯ 中的每一位称为 位 ，记为 n ；
将 10,11,12,⋯ 称为 数字 ，记为 num ；
数字 10 是一个两位数，称此数字的 位数 为 2 ，记为 digit ；
每 digit 位数的起始数字（即：1,10,100,⋯），记为 start 。
个位数共有 1 ~ 9 九个数字，称个位数的 数字数量 为 9 ，记为 num_count 。
十位数共有 10~99 90个数字，每个数字有两位，共占序列化 90*2=180 位，称十位数的 数位数量为 180 ，记为 count 。

可以得到下表（个位数不计入0）：

数字范围	位数	数字数量	共占序列化多少位
1~9	1	9	9
10~99	2	90	180
100~999	3	900	2700
……	……	……	……
start~end	digit	9*start	9 * start * digit

可以得到三个公式：

位数递推公式 digit = digit + 1
起始数字递推公式 start= start * 10
数字数量计算公式 num_count = 9 * start
数位数量计算公式 count = 9 * start * digit

我们可以将求 第n位对应的数字 求解过程分为以下几步：

确定 n 所在 数字 的 位数digit ；
确定 n 所在的 数字num ；
确定 n 是 num 中的哪一位。

第一步：

在几位数的范围内？

while(n>count){n -= count;start *= 10;digit++;count = 9*start*digit;
}

第二步：

是哪个数字？

int num = start+(n-1)/digit;

为什么是 (n-1)/digit 而不是 n/digit ？

首先看一张图：
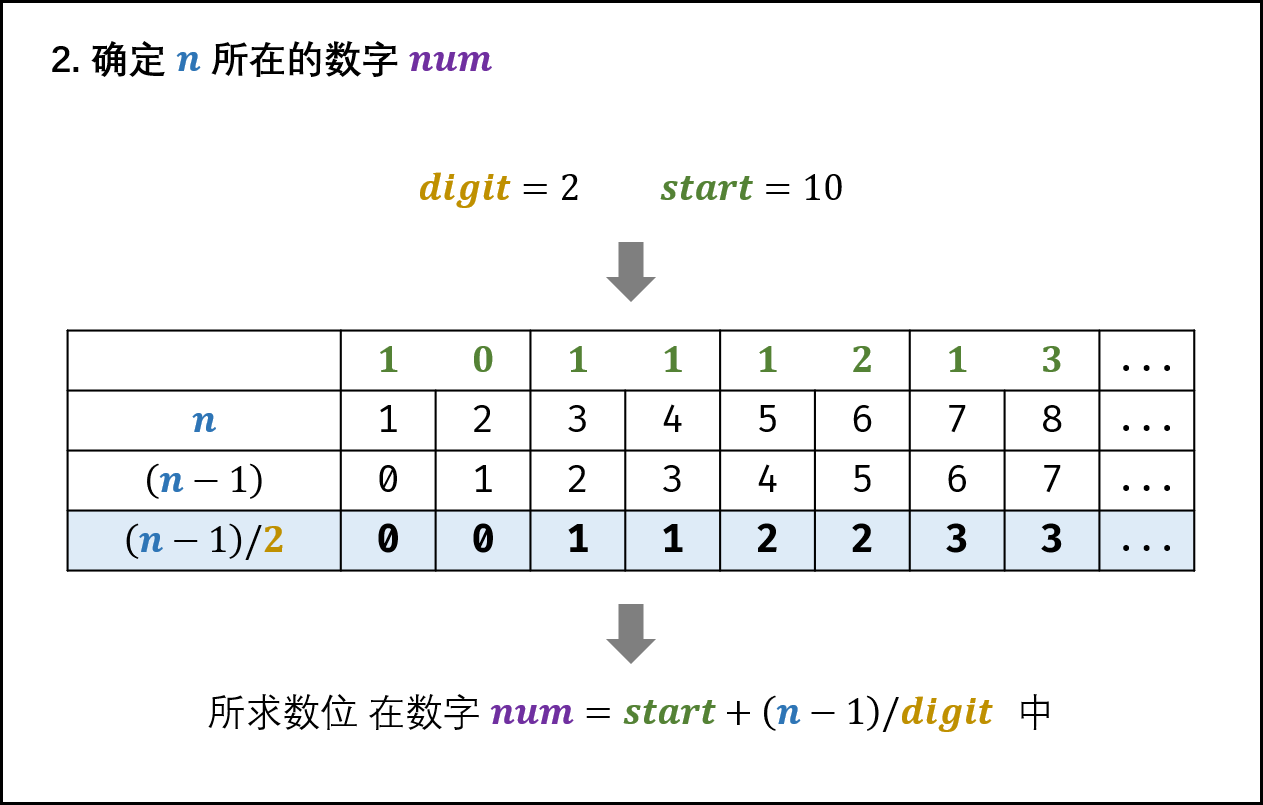
在这里插入图片描述

以两位数为例，当执行完 n=n-9 之后，n 与各个两位数数位的对应关系如上图所示。以13为例，当我们知道 n=7（13中的1） 时，由 n/2=3 可得 n 是十位数起始数字之后的第三个，但是当 n=8（13中的3） 时，由 n/2=4 得到 n 对应的是十位数起始数字之后的第四个，这是错误的，十位数起始数字之后的第四个是 14 而非 13 ，因此计算时需要将 n 进行 减一操作，因为我们将起始数字看作 第0个数 而非 第1个数 。

为什么是 (n-1)/digit 而不是 n/digit-1？

仍然以两位数为例，当 n 对应非起始数字时，两种算法是没有区别的，但是当 n 对应起始数字时，不论 n=0 or n=1 ， (n-1)/digit 的计算结果都为 0 ，而 n/digit-1 的计算结果都为 -1 。 (n-1)/digit 对应的数字 num = start + 0 = 10 ，正确；而 n/digit-1 对应的数字 num = start + (-1) = 9 ，变成了个位数，错误。

总而言之，对 n 进行 减一操作 是因为 起始数字应视为 start + 0，虽然它是两位数里面的 第一个 数字，但是我们在公式里说的 第几个 是 该数字相对于起始数字 而言的，因此要统统减一。而之所以不是 先除再减 而是 先减再除 是因为 要考虑逻辑顺序对起始数字的影响 。

第三步：

处于对应数字的哪一位？

num = s[(n-1)%digit] - '0';

(n-1)%digit 计算的便是对应的 数位 ，n减一的原因和第二步中相同，不再赘述。

代码

class Solution {
public:int findNthDigit(int n) {long long start=1, count=9, digit=1;while(n>count){n -= count;start *= 10;digit++;count = 9*start*digit;}int num = start+(n-1)/digit;//所在数字string s = to_string(num);num = s[(n-1)%digit] - '0';//处于所在num的哪一位return num;}
};