目录
1. 规划简介
2. 将地图转为图形
3. 路径查找算法:A*
4. 轨迹生成
5. Fernet坐标系
本文转自微信公众号:Apollo开发者社区 原创: 阿波君 Apollo开发者社区 9月13日
上周我们发布了无人驾驶技术的 预测篇,简要介绍了预测的主要方法以及递归神经网络在预测中的应用。随着知识讲解的深入,越来越多的开发者加入到了Apollo学习交流社群中。希望开发者们可以充分利用Apollo平台,在吸收新知识的同时碰撞出思维的火花。
本期我们将介绍路径规划。在规划中我们将结合高精度地图、定位和预测的相关知识,从路线导航和轨迹生成两方面来构建车辆轨迹。
视频链接为:Apollo自动驾驶入门课程Sebastian规划_腾讯视频
1. 规划简介
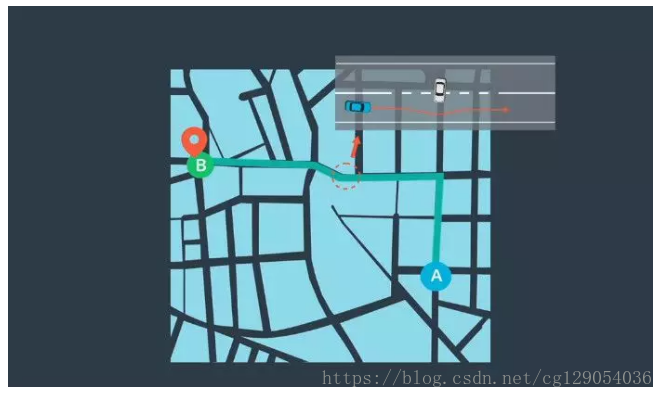
路径规划是指通过一定的规则,找到一条通过世界的路径来达到我们想去的地方。规划的第一步是路线导航,侧重于研究如何从地图上的A点前往B点。在路线导航时,将地图数据作为输入,并输出可行驶路径。手机导航系统是路线导航的一个示例。在Apollo中,可以通过路线规划模块处理该任务。一旦我们构建出高水平的路线,我们就会放大至轨迹规划。该轨迹由一系列点定义,每个点都有一个关联速度和一个指示何时应抵达那个点的时间戳。通过轨迹规划,我们可以做出微妙的决策,以避开障碍物,并为乘客创造平稳的乘车体验。在Apollo中,我们通过规划模块处理该任务。路线规划的目标是,找到从地图上的A前往B的最佳路径。轨迹规划的目标是找到避免碰撞和保持舒适度的可执行轨迹。
路径规划使用三个输入,第一个输入为地图,Apollo提供的地图数据包括公路网和实时交通信息。第二个输入为我们当前在地图上的位置。第三个输入为我们的目的地,目的地取决于车辆中的乘客。
2. 将地图转为图形
当人们试图在地图上找到从A到B的路线时,通常会沿着道路追踪路径,以查看是否存在通往目的地的任何路径,这被称为搜索。Apollo也通过搜索来查找路线,但它使用了更智能的搜索算法。在进行智能搜索算法以前,我们需要将地图数据重新格式化为“图形”的数据结构。
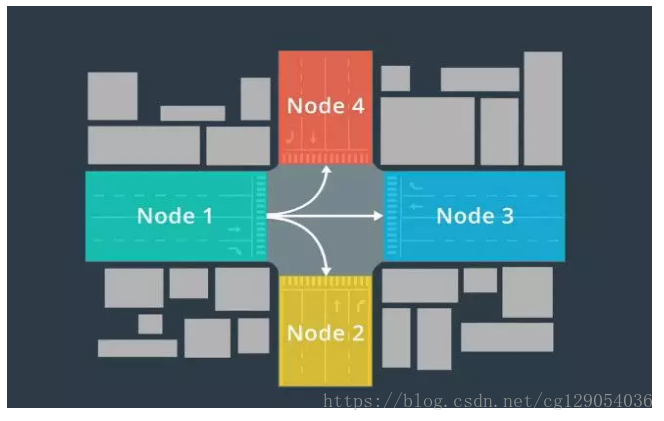
该图形由“节点”(node)和“边缘”(edge)组成。节点代表路段,边缘代表这些路段之间的连接。例如:在交叉路口,汽车可从节点1移动到节点2、节点3或节点4,反之亦然。
我们可以对一个节点移动到另一个节点所需的成本进行建模。例如在现实生活中,拐过一个交叉路口比直行更费劲,所以从节点1到节点4的成本高于从节点1到节点3的成本。 将地图转换为图形的好处在于,在计算机科学领域中,人们已发现许多用于在图形中查找路径的快速算法(下一节中会详细介绍)。一旦我们在图形中找到了一条好路径,就可以轻松地将图形中的路径重新转换为地图上的路径。
3. 路径查找算法:A*
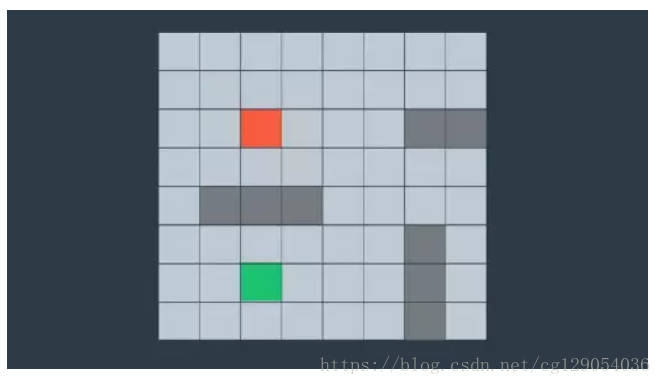
A* 是经典的路径查找处理算法。在本节中,我们将演示A* 如何通过网格进行工作。我们把网格中的每个单元格当作一个节点。并且规定能够从任何一个节点移动到与其相邻的任意节点。这个特殊网格还包含一些阻挡潜在路径的墙壁(下图中的灰色部分)。
对人类来说,通过查看图形便可以轻易找出最佳路径。但对于计算机而言,这并不明显。计算机必须确认是否存在通往目的地的路径,并竭尽所能地尝试所有可能的路径来从其中选出最优路径。但是,这需要耗费大量的时间,尤其是在地图非常大的时候。从任何给定的节点来看,最多有8个用于下一步的选项,因为存在8个相邻的单元格。对于8个中的每一个选项,下一步又有另外8个选项。如果我们展开所有节点,搜索量将暴增至即使最快的计算机也无法处理的程度。
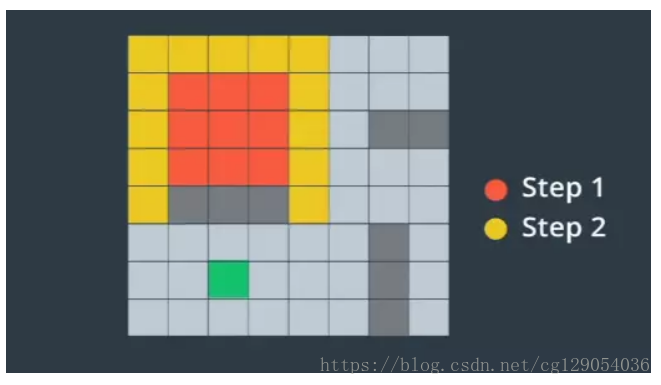
下面我们将展示A*算法的详细过程(如下图):从初始节点开始,我们需要确定8个相邻节点中,哪个是最有希望的候选节点。对于每个候选节点,我们考虑两件事情。首先,我们计算从开始节点到候选节点的成本。然后,我们估计从候选节点前往目的地的成本。计算前往候选节点的成本很容易,因为它已经与我们相邻。计算从候选节点到目的地的成本很困难。但是,通过简单计算从候选节点到目的地的距离,我们通常可以做出很好的估计。
我们用变量g和h表示每个成本。g值为开始节点前往候选节点的成本,h值为候选节点前往目的地的估计成本或启发式成本。根据我们的具体情况,我们可以自定义成本估算方式。例如,交通堵塞会增加前往目的地的成本,所以交通繁忙的路径具有更高的成本。对于每个候选节点,我们通过添加g值和h值来计算总和,即f值。最佳候选节点是f值最小的节点。每当我们抵达新节点时,我们通过重复此过程来选择下一个候选节点,而且总是选择我们尚未访问过且具有最小f值的节点。这就是A* 算法,它建立了一条稳定前往目的地的路径。
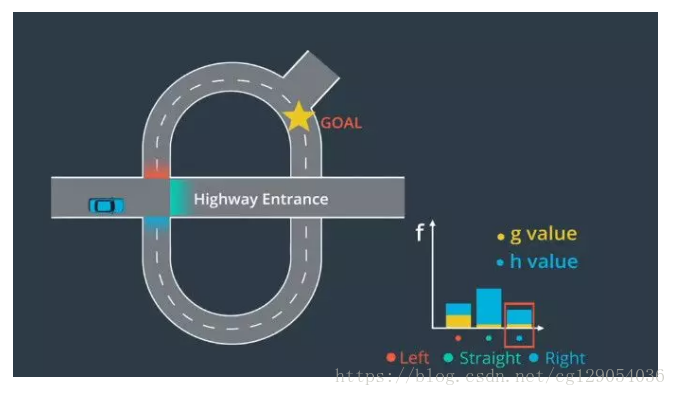
现在我们来考虑一下现实世界中的地图。
假设我们到达了一个交叉路口,我们可以沿着公路直走、左转或右转。首先,我们将把这张地图转换为具有三个候选节点(left,straight,right)的图形。接下来,我们将对选项进行评估。在实践中,拐过交叉路口很费劲,所以我们为left节点分配了更高的g值(g值表示从起始点到候选节点的成本)。在查看公路选项之后,我们意识到必须走很长的路,才能离开公路并返回我们的目标,所以我们为straight选项分配了更高的h值(h值表示从候选节点到目的地的估计成本)。最后,我们通过将g值和h值相加来计算每个节点的f值。我们看到最低f值实际对应右边的候选节点。所以,这是我们接下来要前往的节点。
4. 轨迹生成
高等级地图路线只是规划过程中的一部分,我们仍需要构建沿这条路线前进的低等级轨迹。这意味着要处理一些不属于地图的物体:如其他车辆、自行车或行人。例如,我们可能需要与试图在我们前面掉头的汽车互动,或者我们可能希望超过一辆在公路上行驶的慢车。这些场景需要更低级别、更高精确度的规划。我们将这一级别的规划称为轨迹生成。
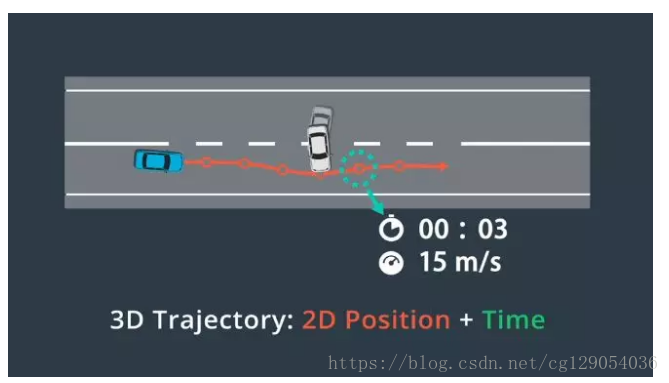
轨迹生成的目标是生成一系列路径点所定义的轨迹。我们为每个路径点分配了一个时间戳和速度。由于移动的障碍物可能会暂时阻挡部分路段,轨迹中的每个路径点都有时间戳。我们可以将时间戳与预测模块的输出相结合,以确保我们计划通过时,轨迹上的每个路径点均未被占用。这些时间戳和空间上的两个维度(2D position)共同创建了一个三维轨迹(3D Trajectory)。我们还为每个路径点指定了一个速度,用于确保车辆按时到达每个路径点。
现实世界中的规划面临多种约束。首先轨迹应能免于碰撞,这意味着必须没有障碍物。其次,要让乘客感到舒适,所以路径点之间的过渡以及速度的任何变化都必须平滑。再者,路径点对车辆应实际可行,例如高速行驶的汽车不能立即做180度转弯。我们不能构建包含这种不可行机动的轨迹。最后,轨迹应合法。我们需要了解每个路径点的交通法律,并确保轨迹遵守这些法律法规。
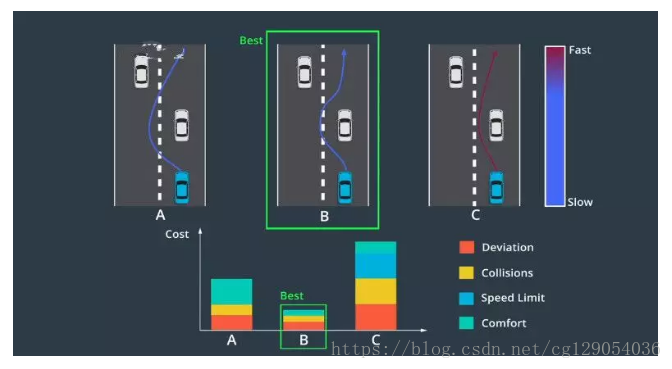
在道路的任何两点,可能会有多个不会发生碰撞、行驶舒适、可行且合法的轨迹。我们如何选择最佳轨迹呢?答案是使用“成本函数”。成本函数为每个轨迹分配了一个“成本”,我们选择成本最低的轨迹。轨迹“成本”由各种犯规处罚组成,例如:偏离道路中心,有可能产生碰撞,速度限制,轨迹的曲率和加速度让乘客感到不舒服等。
轨迹成本将所有这些缺陷聚合为单个数字,这使我们能对不同的轨迹按数字大小进行排名。车辆甚至可能在不同的环境中使用不同的成本函数。例如,高速路的成本函数可能与停车场的不同。
5. Fernet坐标系
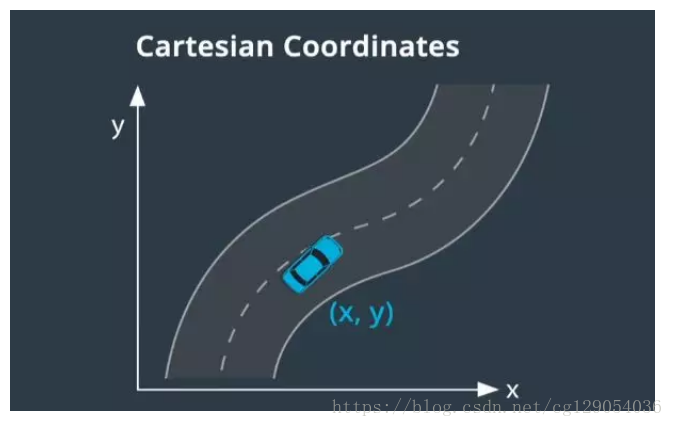
我们通常使用笛卡尔坐标系描述物体的位置,但笛卡尔坐标系对车辆来说并不是最佳选择。即使给出了车辆位置(x,y),如果我们不知道道路在哪,就很难知道车辆行驶了多远也很难知道车辆是否偏离了道路中心。
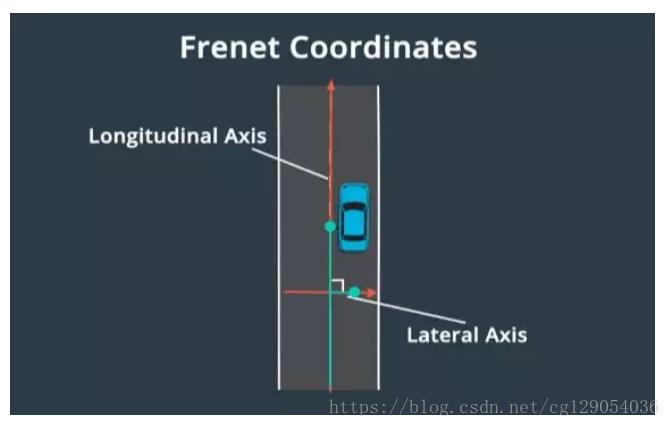
笛卡尔坐标系的替代解决方案为Frenet坐标系。Frenet坐标系描述了汽车相对于道路的位置。在Frenet框架中,s代表沿道路的距离,也被称为纵坐标。d表示与纵向线的位移,也被称为横坐标。在道路的每个点上,横轴和纵轴都是垂直的。纵坐标表示道路中的行驶距离,横坐标表示汽车偏离中心线的距离。
更多详细课程内容,大家可以登陆官网继续学习!
也可以添加社区小助手(Apollodev)为好友,回复“课程学习”进群与其他开发者共同交流学习。
自课程上线以来,浏览量已超10万,已帮助全球97个国家约 7000 名学员入门自动驾驶与 Apollo 开源平台,其中37%为海外学员,本门课程已成为优达学城 (Udacity) 近期获得关注度最高的免费课程之一。




)
)
:快速理解为什么说UDP有时比TCP更有优势)

)
:史上最通俗的集线器、交换机、路由器功能原理入门)
报错VM71:1 Uncaught SyntaxError: Unexpected token u in JSON at position 0等之类的问题)
)

:深入浅出,全面理解HTTP协议)
)


)


:手把手教你写基于TCP的Socket长连接)
)
