目录

1）使用狄克斯特拉算法

2）术语

3）实现

4）小结

---

本章内容;

•        介绍加权图，提高或降低某些边的权重；
•        介绍狄克斯特拉算法，找出加权图中前往X的最短路径；
•        介绍图中的环，它导致狄克斯特拉算法不管用；

在上一篇博客中，我们找到了从A到B的路径，这是最短路径，只有三段，但不一定是最短路径。

广度优先搜索可以找出段数最少的路径，但如果要找出最快的路径，可使用狄克斯特拉算法。

1）使用狄克斯特拉算法

还是来看一个例子，如何对下面的图使用这种算法。图中每个数字表示的是时间，单位是分钟。如果使用广度优先搜索算法，将得到下面这条段数最少的路径。

狄克斯特拉算法包括4个步骤：

1. 找出“最便宜”的节点，即可在最短时间内到达的节点。
2. 更新该节点的邻居的开销，其含义稍后介绍。
3. 重复这个过程，直到对图中的每个几点都这样做了。
4. 计算最短路径。

第一步：找出最便宜的节点，你站在起点，不知道该前往节点A还是节点B。前往节点A需要6分钟，前往节点B需要2分钟，由于还不知道前往终点需要多长时间，因此假设为无穷大。

    

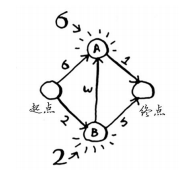
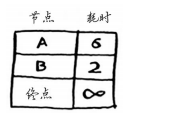
第二步：计算经节点B前往其各个邻居所需的时间。

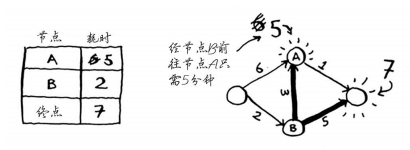
对于节点B的邻居，如果找到前往它的更短路径，就更新其开销。在这里，我们找到了：

前往节点A的更短路径（时间从6分钟缩短到5分钟）。

前往终点的更短路径（时间从无穷大缩短到7分钟）。

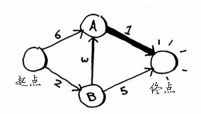
第三步：重复！

现在更新节点A的所有邻居的开销。这时前往终点的时间缩短到6分钟。

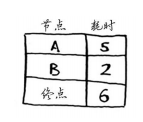
2）术语

狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重（weight）。

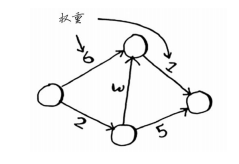
带权重的图称为加权图，不带权重的图称为非加权重。

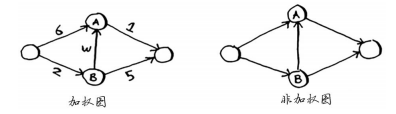
要计算非加权图中的最短路径，可使用广度优先搜索，要计算加权图中的最短路径，可使用狄克斯特拉算法。这里需要指出的时，狄克斯特拉算法只适用与有向无环图。

3）实现

下面来看看如何用代码来实现狄克斯特拉算法。要解决这个问题，需要用到散列表。

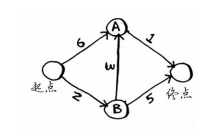
随着算法的进行，不断地更新散列表COSTS和PARENTS。Python实现代码如下：

# the graph
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2graph["a"] = {}
graph["a"]["fin"] = 1graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5graph["fin"] = {}# the costs table
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity# the parents table
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = Noneprocessed = []def find_lowest_cost_node(costs):lowest_cost = float("inf")lowest_cost_node = None# Go through each node.for node in costs:cost = costs[node]# If it's the lowest cost so far and hasn't been processed yet...if cost < lowest_cost and node not in processed:# ... set it as the new lowest-cost node.lowest_cost = costlowest_cost_node = nodereturn lowest_cost_node# Find the lowest-cost node that you haven't processed yet.
node = find_lowest_cost_node(costs)
# If you've processed all the nodes, this while loop is done.
while node is not None:cost = costs[node]# Go through all the neighbors of this node.neighbors = graph[node]for n in neighbors.keys():new_cost = cost + neighbors[n]# If it's cheaper to get to this neighbor by going through this node...if costs[n] > new_cost:# ... update the cost for this node.costs[n] = new_cost# This node becomes the new parent for this neighbor.parents[n] = node# Mark the node as processed.processed.append(node)# Find the next node to process, and loop.node = find_lowest_cost_node(costs)print "Cost from the start to each node:"
print costs

4）小结

1. 广度优先搜索用于在非加权图中查找最短路径。
2. 狄克斯特拉算法用于在加权图中查找最短路径。
3. 仅当权重为正时狄克斯特拉算法才管用。
4. 如果图中包含负权边，请使用贝尔曼---福德算法。