目录

（1）背包问题

（2）最长公共子串

（3）小结

---

本章内容：

• 学习动态规划，它将问题分成小问题，并先着手解决这些小问题。
• 学习如何设计问题的动态规划解决方案。

（1）背包问题

我们再看第八章的背包问题，假设你是个小偷，为了让盗窃的商品价值最高，你该选择哪些商品？最简单的算法如下：尝试各种可能的商品组合，并找出价值最高的组合。

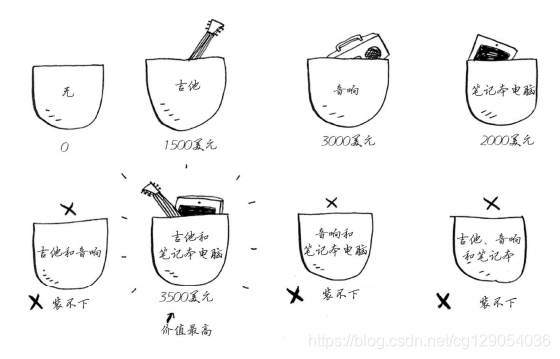
这样可行，但速度非常慢！每增加一件商品，需要计算得集合数都将翻倍！

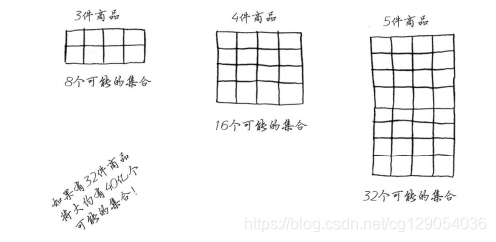
那么如何找到最优解呢！答案是使用动态规划！动态规划先解决子问题，再逐步解决大问题！

每个动态规划算法都从一个网格开始，背包问题的网格如下！

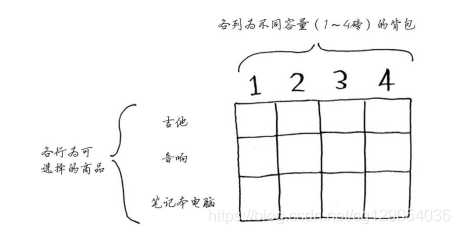
网格的各行为商品，各列为不同容量（1-4磅）的背包。所有这些列你都需要，因为它们将帮助你计算子背包的价值。网格最初是空的，你将填充其中的每个单元格，网格填满后，就找到了问题的答案！你一定要跟着做。请你创建网格，我们一起 来填满它。

1.吉他行

下面来开始填充网格，第一个单元格表示背包的容量为1磅，吉他的重量是1磅，这意味着它能装入背包！因此这个单元格包含吉他，价值为1500美元。

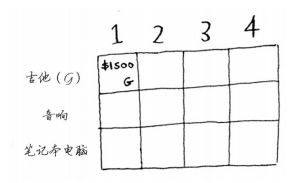
下面来看下一个单元格，这个单元格表示背包的容量为2磅，完全能够装下吉他！

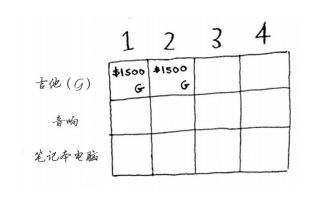
这里的其他单元格也一样，别忘了，这是第一行，只有吉他可供选择。

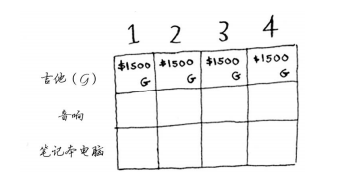
如果我们有一个容量为4磅的背包，可在其中装入的商品的最大价值为1500美元。但这不是最优解。

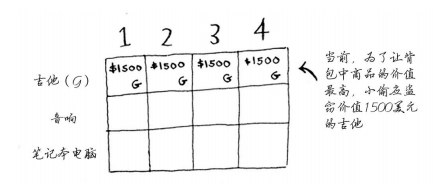
2.音响行

你现在位于第二行，可偷的商品有吉他和音响。在每一行，可偷的商品都为当前行的商品以及之前各行的商品。因此，当前你只能偷音响和吉他。我们来看第一个单元格。

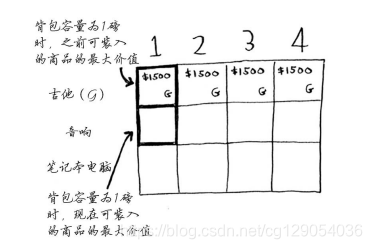
该不该偷音响呢？背包的容量为1磅，能装下音响吗?音响太重了，装不下！由于容量1磅的背包装不下音响，因此最大价值仍然是1500美元。

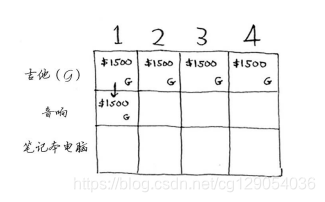
接下来的两个单元格的情况与此相同。在这些单元格中，背包的容量分别为2磅和3磅，由于这些背包装不下音响，因此最大价值保持不变。

 

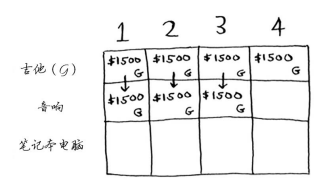
背包容量为4磅呢？终于能够装下音响了！原来的最大价值为1500美元，但如果在背包中装入音响而不是吉他，价值将为3000美元！因此还是偷音响吧。

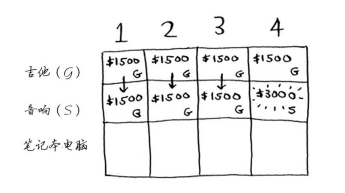
后面，我们将会逐步的更新最大价值！

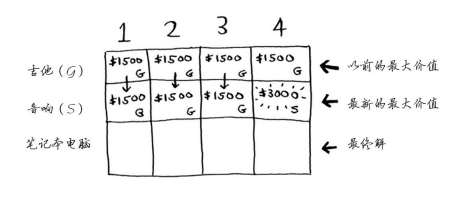
3.笔记本电脑行

笔记本电脑重3磅，没法将其装入容量为1磅或2磅的背包，因此前两个单元格的最大价值还是1500美元。

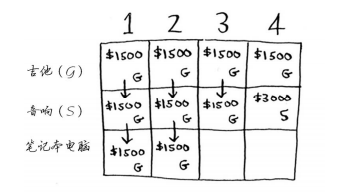
对于容量为3磅的背包，最大价值将为2000美元！

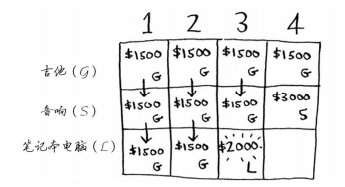
对于容量为4磅的背包，情况很有趣，这是非常重要的部分，当前的最大价值为3000美元。根据之前计算的最大价值可知，在1磅的容量中可装入吉他，价值为1500美元。因此，你需要做下比较：

最终的网格类似于下面这样：

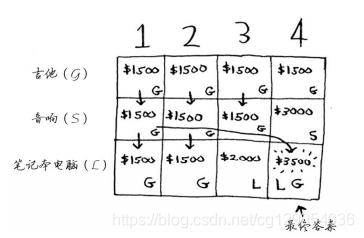
（2）最长公共子串

通过前面的动态规划问题，可以得到如下启示：

1. 动态规划可帮助你在给定约束条件下得到最优解。
2. 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。
3. 每种动态规划解决方案都涉及网格。
4. 单元格中德值通常就是你要优化的值。
5. 每个单元格都是一个子问题。

下面再来看一个例子，假设你管理着一个网站，用户在该网站输入单词时，你需要给出其定义。但如果用户拼错了，你必须猜测他原本要输入的是什么单词，例如fish和hish。

1.绘制网格

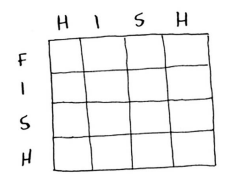
2.填充网格

下面是这个单元格的一部分：

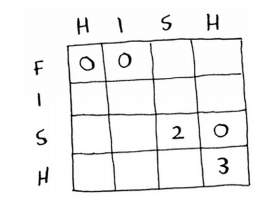
3.揭晓答案

我们使用如下公式来计算每个单元格的值。

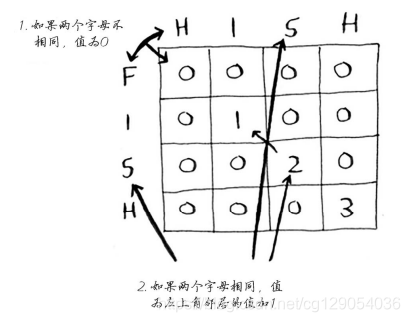
最终的单元格如下：

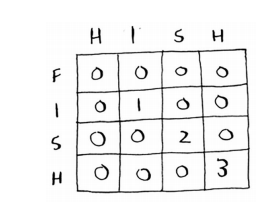
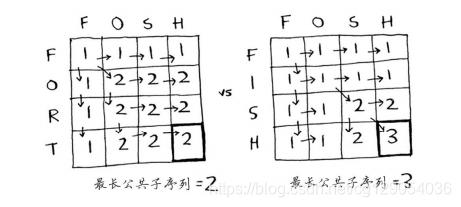
4.最长公共子序列之解决方案

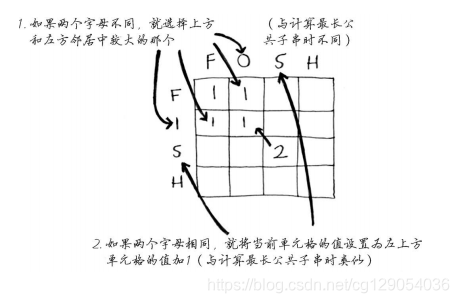
最终的网格如下：

（3）小结

1. 需要在给定约束条件下优化某种指标时，动态规划很有用。
2. 问题可分解为离散子问题时，可使用动态规划来解决。
3. 每种动态规划解决方案都涉及网格。
4. 单元格中的值通常就是你要优化的值。
5. 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
6. 没有放之四海皆准的计算动态规划解决方案的公式。