题目链接:斐波那契数列 - 题目 - 青藤 OJ
题目来源:经典题
题目大意
输入
这里我们不讨论递推方法,我们采用这道简单的题目简单说一下记忆化搜索相关内容。
解法
首先,基础的递归解决的程序非常好写,对于 f(n) 来说
- 边界情况:
- 递归方程:
所以代码就很自然
#include <bits/stdc++.h>
using namespace std;
long long f(int n) {if (n == 1)return 0;if (n == 2)return 1;return f(n - 1) + f(n - 2);
}
int main() {int n;cin >> n;cout << f(n) << endl;return 0;
}
然而这样的做法,在 n 为 40 时便达到了 500ms,在 45 时无法通过,为什么呢?
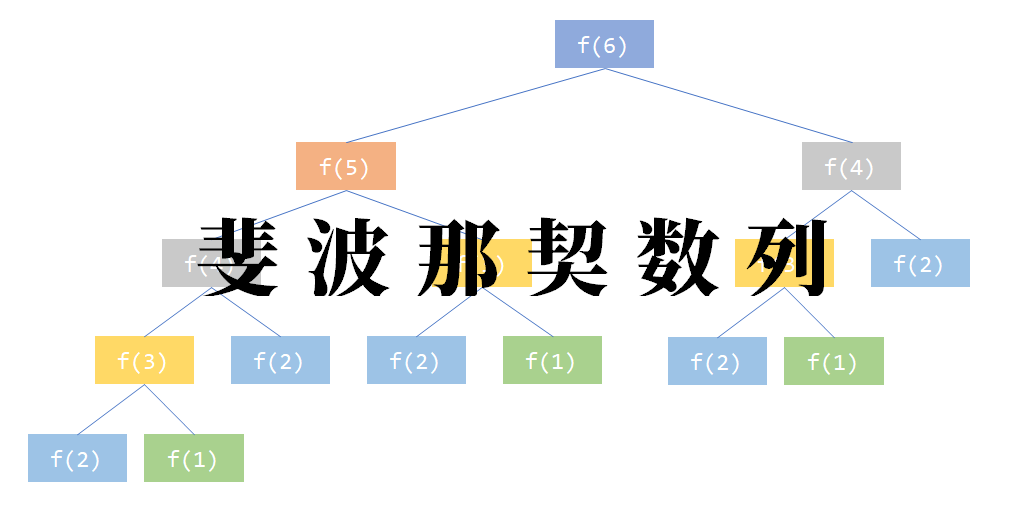
我们会发现,求解 f(6) 时 用到的 f(4) 会在求解 f(5) 用到时重新求解,再往上看的话,重复计算所花的时间时非常恐怖的,导致我们做了很多多余的计算。
解决的方法也很简单,算过了的我们就拿个小本本出来记下来,下次要用上直接拿出上次的结果就好。
#include <bits/stdc++.h>
using namespace std;
long long book[50]; //小本本
long long f(int n) {//如果算过了,直接返回结果if (book[n] != -1)return book[n];if (n == 1) {//返回之前记下来book[n] = 0;return book[n];}if (n == 2) {//返回之前记下来book[n] = 1;return 1;}//返回之前记下来book[n] = f(n - 1) + f(n - 2);return book[n];
}
int main() {//没算过的就用-1表示memset(book, -1, sizeof(book));int n;cin >> n;cout << f(n) << endl;return 0;
}
这便是所谓的记忆化递归。如果有两个参数的递归我们可以开一个二维数组来记录就好。
比如下面这道:阿克曼(Ackmann)函数 - 题目 - 青藤 OJ
虽然这道题的数据范围不需要记忆化,普通递归也能过,但是大家可以试一下用记忆化递归实现~
当然斐波那契数列的求解还会有更多方式,递推的方式就可以和记忆化递归一样达到
-socket)
)





)

低层次点云处理)
)

)


` Maven repository from your build scripts and migrate your build)



