主成分分析
引言
主成分分析(PCA)是一种能够极大提升无监督特征学习速度的数据降维算法。更重要的是,理解PCA算法,对实现白化算法有很大的帮助,很多算法都先用白化算法作预处理步骤。
假设你使用图像来训练算法,因为图像中相邻的像素高度相关,输入数据是有一定冗余的。具体来说,假如我们正在训练的16x16灰度值图像,记为一个256维向量 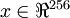 ,其中特征值
,其中特征值 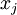 对应每个像素的亮度值。由于相邻像素间的相关性,PCA算法可以将输入向量转换为一个维数低很多的近似向量,而且误差非常小。
对应每个像素的亮度值。由于相邻像素间的相关性,PCA算法可以将输入向量转换为一个维数低很多的近似向量,而且误差非常小。
实例和数学背景
在我们的实例中,使用的输入数据集表示为 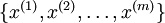 ,维度
,维度 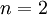 即
即 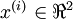 。假设我们想把数据从2维降到1维。(在实际应用中,我们也许需要把数据从256维降到50维;在这里使用低维数据,主要是为了更好地可视化算法的行为)。下图是我们的数据集:
。假设我们想把数据从2维降到1维。(在实际应用中,我们也许需要把数据从256维降到50维;在这里使用低维数据,主要是为了更好地可视化算法的行为)。下图是我们的数据集:
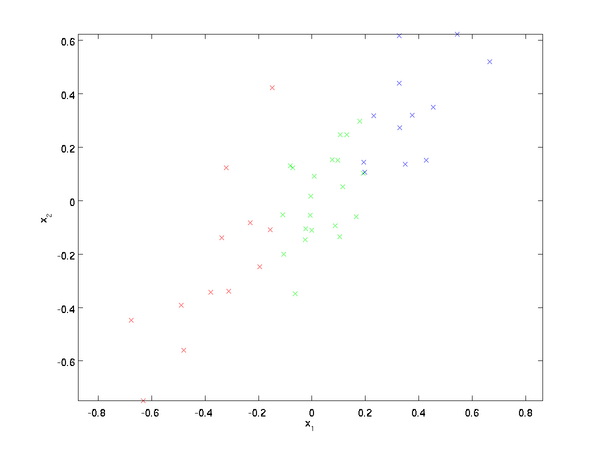
这些数据已经进行了预处理,使得每个特征 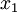 和
和 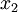 具有相同的均值(零)和方差。
具有相同的均值(零)和方差。
为方便展示,根据 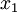 值的大小,我们将每个点分别涂上了三种颜色之一,但该颜色并不用于算法而仅用于图解。
值的大小,我们将每个点分别涂上了三种颜色之一,但该颜色并不用于算法而仅用于图解。
PCA算法将寻找一个低维空间来投影我们的数据。从下图中可以看出, 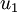 是数据变化的主方向,而
是数据变化的主方向,而 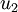 是次方向。
是次方向。
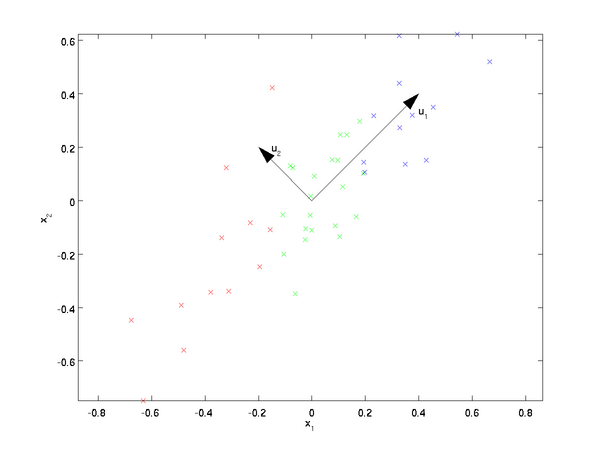
也就是说,数据在 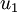 方向上的变化要比在
方向上的变化要比在 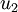 方向上大。为更形式化地找出方向
方向上大。为更形式化地找出方向 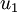 和
和 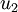 ,我们首先计算出矩阵
,我们首先计算出矩阵 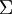 ,如下所示:
,如下所示:
假设  的均值为零,那么
的均值为零,那么 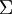 就是x的协方差矩阵。(符号
就是x的协方差矩阵。(符号 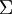 ,读"Sigma",是协方差矩阵的标准符号。虽然看起来与求和符号
,读"Sigma",是协方差矩阵的标准符号。虽然看起来与求和符号 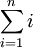 比较像,但它们其实是两个不同的概念。)
比较像,但它们其实是两个不同的概念。)
可以证明,数据变化的主方向 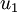 就是协方差矩阵
就是协方差矩阵 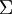 的主特征向量,而
的主特征向量,而 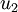 是次特征向量。
是次特征向量。
注:如果你对如何得到这个结果的具体数学推导过程感兴趣,可以参看CS229(机器学习)PCA部分的课件(链接在本页底部)。但如果仅仅是想跟上本课,可以不必如此。
你可以通过标准的数值线性代数运算软件求得特征向量(见实现说明).我们先计算出协方差矩阵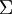 的特征向量,按列排放,而组成矩阵
的特征向量,按列排放,而组成矩阵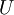 :
:
此处, 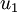 是主特征向量(对应最大的特征值),
是主特征向量(对应最大的特征值), 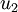 是次特征向量。以此类推,另记
是次特征向量。以此类推,另记 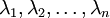 为相应的特征值。
为相应的特征值。
在本例中,向量 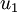 和
和 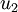 构成了一个新基,可以用来表示数据。令
构成了一个新基,可以用来表示数据。令 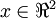 为训练样本,那么
为训练样本,那么 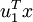 就是样本点
就是样本点  在维度
在维度 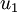 上的投影的长度(幅值)。同样的,
上的投影的长度(幅值)。同样的, 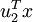 是
是  投影到
投影到 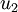 维度上的幅值。
维度上的幅值。
旋转数据
至此,我们可以把  用
用 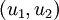 基表达为:
基表达为:
(下标“rot”来源于单词“rotation”,意指这是原数据经过旋转(也可以说成映射)后得到的结果)
对数据集中的每个样本  分别进行旋转:
分别进行旋转: 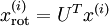 for every
for every  ,然后把变换后的数据
,然后把变换后的数据 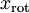 显示在坐标图上,可得:
显示在坐标图上,可得:
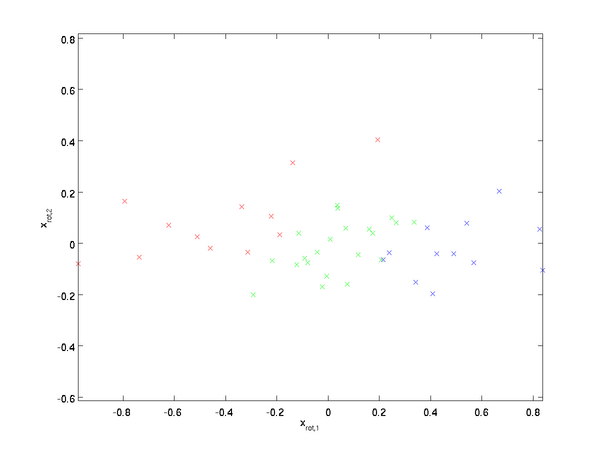
这就是把训练数据集旋转到 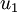 ,
,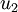 基后的结果。一般而言,运算
基后的结果。一般而言,运算 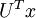 表示旋转到基
表示旋转到基 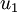 ,
,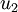 , ...,
, ...,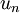 之上的训练数据。矩阵
之上的训练数据。矩阵 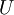 有正交性,即满足
有正交性,即满足 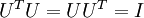 ,所以若想将旋转后的向量
,所以若想将旋转后的向量 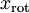 还原为原始数据
还原为原始数据  ,将其左乘矩阵
,将其左乘矩阵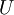 即可:
即可: 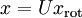 , 验算一下:
, 验算一下: 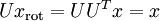 .
.
数据降维
数据的主方向就是旋转数据的第一维 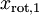 。因此,若想把这数据降到一维,可令:
。因此,若想把这数据降到一维,可令:
更一般的,假如想把数据 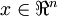 降到
降到  维表示
维表示 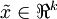 (令
(令 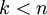 ),只需选取
),只需选取 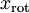 的前
的前  个成分,分别对应前
个成分,分别对应前  个数据变化的主方向。
个数据变化的主方向。
PCA的另外一种解释是: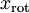 是一个
是一个 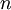 维向量,其中前几个成分可能比较大(例如,上例中大部分样本第一个成分
维向量,其中前几个成分可能比较大(例如,上例中大部分样本第一个成分 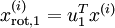 的取值相对较大),而后面成分可能会比较小(例如,上例中大部分样本的
的取值相对较大),而后面成分可能会比较小(例如,上例中大部分样本的 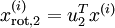 较小)。
较小)。
PCA算法做的其实就是丢弃 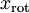 中后面(取值较小)的成分,就是将这些成分的值近似为零。具体的说,设
中后面(取值较小)的成分,就是将这些成分的值近似为零。具体的说,设 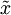 是
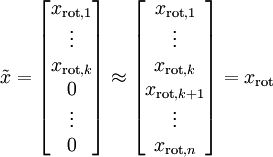
是 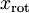 的近似表示,那么将
的近似表示,那么将 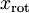 除了前
除了前  个成分外,其余全赋值为零,就得到:
个成分外,其余全赋值为零,就得到:
在本例中,可得 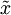 的点图如下(取
的点图如下(取 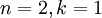 ):
):
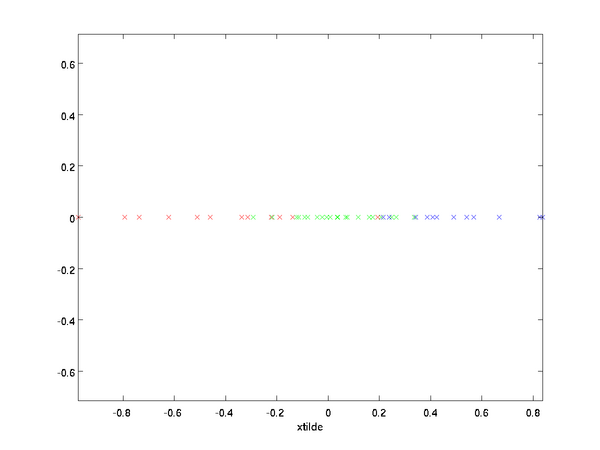
然而,由于上面 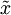 的后
的后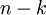 项均为零,没必要把这些零项保留下来。所以,我们仅用前
项均为零,没必要把这些零项保留下来。所以,我们仅用前  个(非零)成分来定义
个(非零)成分来定义  维向量
维向量 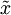 。
。
这也解释了我们为什么会以 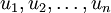 为基来表示数据:要决定保留哪些成分变得很简单,只需取前
为基来表示数据:要决定保留哪些成分变得很简单,只需取前  个成分即可。这时也可以说,我们“保留了前
个成分即可。这时也可以说,我们“保留了前  个PCA(主)成分”。
个PCA(主)成分”。
还原近似数据
现在,我们得到了原始数据 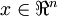 的低维“压缩”表征量
的低维“压缩”表征量 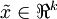 , 反过来,如果给定
, 反过来,如果给定 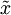 ,我们应如何还原原始数据
,我们应如何还原原始数据  呢?查看以往章节以往章节可知,要转换回来,只需
呢?查看以往章节以往章节可知,要转换回来,只需 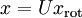 即可。进一步,我们把
即可。进一步,我们把 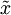 看作将
看作将 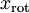 的最后
的最后 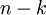 个元素被置0所得的近似表示,因此如果给定
个元素被置0所得的近似表示,因此如果给定 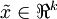 ,可以通过在其末尾添加
,可以通过在其末尾添加 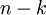 个0来得到对
个0来得到对 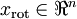 的近似,最后,左乘
的近似,最后,左乘 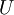 便可近似还原出原数据
便可近似还原出原数据  。具体来说,计算如下:
。具体来说,计算如下:
上面的等式基于先前对 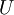 的定义。在实现时,我们实际上并不先给
的定义。在实现时,我们实际上并不先给 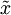 填0然后再左乘
填0然后再左乘 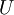 ,因为这意味着大量的乘0运算。我们可用
,因为这意味着大量的乘0运算。我们可用 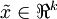 来与
来与 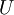 的前
的前  列相乘,即上式中最右项,来达到同样的目的。将该算法应用于本例中的数据集,可得如下关于重构数据
列相乘,即上式中最右项,来达到同样的目的。将该算法应用于本例中的数据集,可得如下关于重构数据 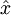 的点图:
的点图:
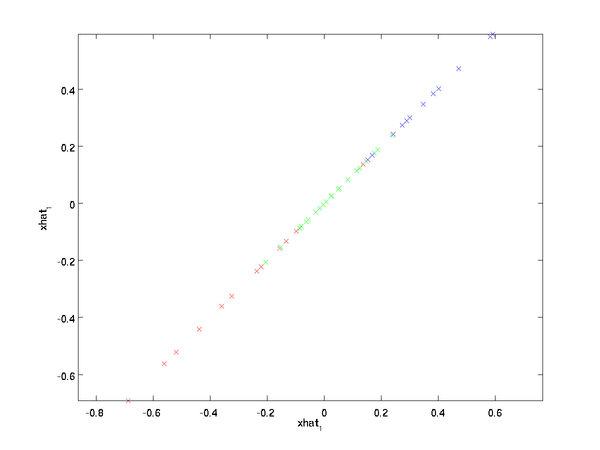
由图可见,我们得到的是对原始数据集的一维近似重构。
在训练自动编码器或其它无监督特征学习算法时,算法运行时间将依赖于输入数据的维数。若用 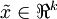 取代
取代  作为输入数据,那么算法就可使用低维数据进行训练,运行速度将显著加快。对于很多数据集来说,低维表征量
作为输入数据,那么算法就可使用低维数据进行训练,运行速度将显著加快。对于很多数据集来说,低维表征量 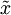 是原数据集的极佳近似,因此在这些场合使用PCA是很合适的,它引入的近似误差的很小,却可显著地提高你算法的运行速度。
是原数据集的极佳近似,因此在这些场合使用PCA是很合适的,它引入的近似误差的很小,却可显著地提高你算法的运行速度。
选择主成分个数
我们该如何选择  ,即保留多少个PCA主成分?在上面这个简单的二维实验中,保留第一个成分看起来是自然的选择。对于高维数据来说,做这个决定就没那么简单:如果
,即保留多少个PCA主成分?在上面这个简单的二维实验中,保留第一个成分看起来是自然的选择。对于高维数据来说,做这个决定就没那么简单:如果  过大,数据压缩率不高,在极限情况
过大,数据压缩率不高,在极限情况 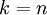 时,等于是在使用原始数据(只是旋转投射到了不同的基);相反地,如果
时,等于是在使用原始数据(只是旋转投射到了不同的基);相反地,如果  过小,那数据的近似误差太太。
过小,那数据的近似误差太太。
决定  值时,我们通常会考虑不同
值时,我们通常会考虑不同  值可保留的方差百分比。具体来说,如果
值可保留的方差百分比。具体来说,如果 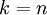 ,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果
,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果 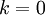 ,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。
,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。
一般而言,设 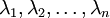 表示
表示 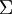 的特征值(按由大到小顺序排列),使得
的特征值(按由大到小顺序排列),使得 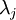 为对应于特征向量
为对应于特征向量 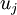 的特征值。那么如果我们保留前
的特征值。那么如果我们保留前  个成分,则保留的方差百分比可计算为:
个成分,则保留的方差百分比可计算为:
在上面简单的二维实验中,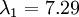 ,
,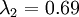 。因此,如果保留
。因此,如果保留 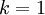 个主成分,等于我们保留了
个主成分,等于我们保留了 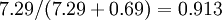 ,即91.3%的方差。
,即91.3%的方差。
对保留方差的百分比进行更正式的定义已超出了本教程的范围,但很容易证明,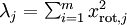 。因此,如果
。因此,如果 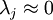 ,则说明
,则说明 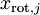 也就基本上接近于0,所以用0来近似它并不会产生多大损失。这也解释了为什么要保留前面的主成分(对应的
也就基本上接近于0,所以用0来近似它并不会产生多大损失。这也解释了为什么要保留前面的主成分(对应的 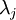 值较大)而不是末尾的那些。 这些前面的主成分
值较大)而不是末尾的那些。 这些前面的主成分 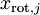 变化性更大,取值也更大,如果将其设为0势必引入较大的近似误差。
变化性更大,取值也更大,如果将其设为0势必引入较大的近似误差。
以处理图像数据为例,一个惯常的经验法则是选择  以保留99%的方差,换句话说,我们选取满足以下条件的最小
以保留99%的方差,换句话说,我们选取满足以下条件的最小  值:
值:
对其它应用,如不介意引入稍大的误差,有时也保留90-98%的方差范围。若向他人介绍PCA算法详情,告诉他们你选择的  保留了95%的方差,比告诉他们你保留了前120个(或任意某个数字)主成分更好理解。
保留了95%的方差,比告诉他们你保留了前120个(或任意某个数字)主成分更好理解。
对图像数据应用PCA算法
为使PCA算法能有效工作,通常我们希望所有的特征 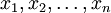 都有相似的取值范围(并且均值接近于0)。如果你曾在其它应用中使用过PCA算法,你可能知道有必要单独对每个特征做预处理,即通过估算每个特征
都有相似的取值范围(并且均值接近于0)。如果你曾在其它应用中使用过PCA算法,你可能知道有必要单独对每个特征做预处理,即通过估算每个特征 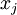 的均值和方差,而后将其取值范围规整化为零均值和单位方差。但是,对于大部分图像类型,我们却不需要进行这样的预处理。假定我们将在自然图像上训练算法,此时特征
的均值和方差,而后将其取值范围规整化为零均值和单位方差。但是,对于大部分图像类型,我们却不需要进行这样的预处理。假定我们将在自然图像上训练算法,此时特征 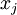 代表的是像素
代表的是像素  的值。所谓“自然图像”,不严格的说,是指人或动物在他们一生中所见的那种图像。
的值。所谓“自然图像”,不严格的说,是指人或动物在他们一生中所见的那种图像。
注:通常我们选取含草木等内容的户外场景图片,然后从中随机截取小图像块(如16x16像素)来训练算法。在实践中我们发现,大多数特征学习算法对训练图片的确切类型并不敏感,所以大多数用普通照相机拍摄的图片,只要不是特别的模糊或带有非常奇怪的人工痕迹,都可以使用。
在自然图像上进行训练时,对每一个像素单独估计均值和方差意义不大,因为(理论上)图像任一部分的统计性质都应该和其它部分相同,图像的这种特性被称作平稳性(stationarity)。
具体而言,为使PCA算法正常工作,我们通常需要满足以下要求:(1)特征的均值大致为0;(2)不同特征的方差值彼此相似。对于自然图片,即使不进行方差归一化操作,条件(2)也自然满足,故而我们不再进行任何方差归一化操作(对音频数据,如声谱,或文本数据,如词袋向量,我们通常也不进行方差归一化)。实际上,PCA算法对输入数据具有缩放不变性,无论输入数据的值被如何放大(或缩小),返回的特征向量都不改变。更正式的说:如果将每个特征向量  都乘以某个正数(即所有特征量被放大或缩小相同的倍数),PCA的输出特征向量都将不会发生变化。
都乘以某个正数(即所有特征量被放大或缩小相同的倍数),PCA的输出特征向量都将不会发生变化。
既然我们不做方差归一化,唯一还需进行的规整化操作就是均值规整化,其目的是保证所有特征的均值都在0附近。根据应用,在大多数情况下,我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中,图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式地说,我们对图像块的平均亮度值不感兴趣,所以可以减去这个值来进行均值规整化。
具体的步骤是,如果 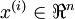 代表16x16的图像块的亮度(灰度)值(
代表16x16的图像块的亮度(灰度)值( 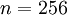 ),可用如下算法来对每幅图像进行零均值化操作:
),可用如下算法来对每幅图像进行零均值化操作:
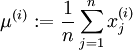
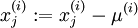 , for all
, for all 
请注意:1)对每个输入图像块 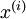 都要单独执行上面两个步骤,2)这里的
都要单独执行上面两个步骤,2)这里的 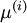 是指图像块
是指图像块 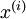 的平均亮度值。尤其需要注意的是,这和为每个像素
的平均亮度值。尤其需要注意的是,这和为每个像素 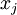 单独估算均值是两个完全不同的概念。
单独估算均值是两个完全不同的概念。
如果你处理的图像并非自然图像(比如,手写文字,或者白背景正中摆放单独物体),其他规整化操作就值得考虑了,而哪种做法最合适也取决于具体应用场合。但对自然图像而言,对每幅图像进行上述的零均值规整化,是默认而合理的处理。
白化
介绍
我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤,这个预处理过程称为白化(一些文献中也叫sphering)。举例来说,假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性;更正式的说,我们希望通过白化过程使得学习算法的输入具有如下性质:(i)特征之间相关性较低;(ii)所有特征具有相同的方差。
2D 的例子
下面我们先用前文的2D例子描述白化的主要思想,然后分别介绍如何将白化与平滑和PCA相结合。
如何消除输入特征之间的相关性? 在前文计算 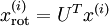 时实际上已经消除了输入特征
时实际上已经消除了输入特征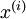 之间的相关性。得到的新特征
之间的相关性。得到的新特征 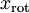 的分布如下图所示:
的分布如下图所示:

这个数据的协方差矩阵如下:
(注: 严格地讲, 这部分许多关于“协方差”的陈述仅当数据均值为0时成立。下文的论述都隐式地假定这一条件成立。不过即使数据均值不为0,下文的说法仍然成立,所以你无需担心这个。)
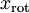 协方差矩阵对角元素的值为
协方差矩阵对角元素的值为 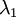 和
和 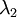 绝非偶然。并且非对角元素值为0; 因此,
绝非偶然。并且非对角元素值为0; 因此, 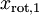 和
和 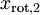 是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。
是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。
为了使每个输入特征具有单位方差,我们可以直接使用 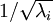 作为缩放因子来缩放每个特征
作为缩放因子来缩放每个特征 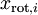 。具体地,我们定义白化后的数据
。具体地,我们定义白化后的数据 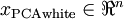 如下:
如下:
绘制出 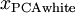 ,我们得到:
,我们得到:
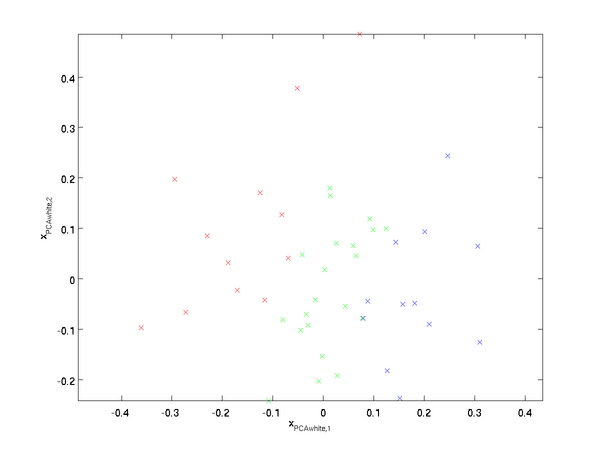
这些数据现在的协方差矩阵为单位矩阵 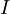 。我们说,
。我们说,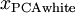 是数据经过PCA白化后的版本:
是数据经过PCA白化后的版本: 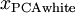 中不同的特征之间不相关并且具有单位方差。
中不同的特征之间不相关并且具有单位方差。
白化与降维相结合。 如果你想要得到经过白化后的数据,并且比初始输入维数更低,可以仅保留 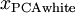 中前
中前  个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论),
个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论),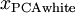 中最后的少量成分将总是接近于0,因而舍弃这些成分不会带来很大的问题。
中最后的少量成分将总是接近于0,因而舍弃这些成分不会带来很大的问题。
ZCA白化
最后要说明的是,使数据的协方差矩阵变为单位矩阵 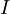 的方式并不唯一。具体地,如果
的方式并不唯一。具体地,如果 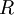 是任意正交矩阵,即满足
是任意正交矩阵,即满足 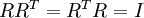 (说它正交不太严格,
(说它正交不太严格,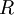 可以是旋转或反射矩阵), 那么
可以是旋转或反射矩阵), 那么 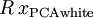 仍然具有单位协方差。在ZCA白化中,令
仍然具有单位协方差。在ZCA白化中,令 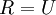 。我们定义ZCA白化的结果为:
。我们定义ZCA白化的结果为:
绘制 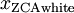 ,得到:
,得到:
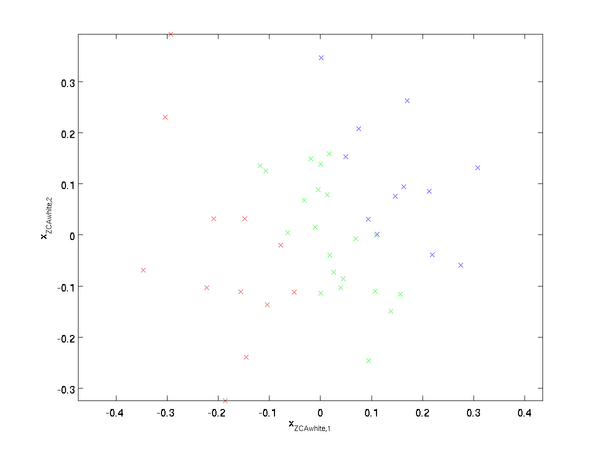
可以证明,对所有可能的 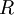 ,这种旋转使得
,这种旋转使得 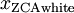 尽可能地接近原始输入数据
尽可能地接近原始输入数据  。
。
当使用 ZCA白化时(不同于 PCA白化),我们通常保留数据的全部 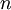 个维度,不尝试去降低它的维数。
个维度,不尝试去降低它的维数。
正则化
实践中需要实现PCA白化或ZCA白化时,有时一些特征值 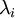 在数值上接近于0,这样在缩放步骤时我们除以
在数值上接近于0,这样在缩放步骤时我们除以 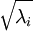 将导致除以一个接近0的值;这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数
将导致除以一个接近0的值;这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数 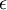 :
:
当  在区间
在区间 ![\textstyle [-1,1]](http://deeplearning.stanford.edu/wiki/images/math/8/5/a/85a1c5a07f21a9eebbfb1dca380f8d38.png) 上时, 一般取值为
上时, 一般取值为 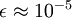 。
。
对图像来说, 这里加上 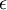 ,对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声,改善学习到的特征(细节超出了本文的范围)。
,对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声,改善学习到的特征(细节超出了本文的范围)。
ZCA 白化是一种数据预处理方法,它将数据从  映射到
映射到 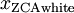 。 事实证明这也是一种生物眼睛(视网膜)处理图像的粗糙模型。具体而言,当你的眼睛感知图像时,由于一幅图像中相邻的部分在亮度上十分相关,大多数临近的“像素”在眼中被感知为相近的值。因此,如果人眼需要分别传输每个像素值(通过视觉神经)到大脑中,会非常不划算。取而代之的是,视网膜进行一个与ZCA中相似的去相关操作 (这是由视网膜上的ON-型和OFF-型光感受器细胞将光信号转变为神经信号完成的)。由此得到对输入图像的更低冗余的表示,并将它传输到大脑。
。 事实证明这也是一种生物眼睛(视网膜)处理图像的粗糙模型。具体而言,当你的眼睛感知图像时,由于一幅图像中相邻的部分在亮度上十分相关,大多数临近的“像素”在眼中被感知为相近的值。因此,如果人眼需要分别传输每个像素值(通过视觉神经)到大脑中,会非常不划算。取而代之的是,视网膜进行一个与ZCA中相似的去相关操作 (这是由视网膜上的ON-型和OFF-型光感受器细胞将光信号转变为神经信号完成的)。由此得到对输入图像的更低冗余的表示,并将它传输到大脑。
实现主成分分析和白化
在这一节里,我们将总结PCA, PCA白化和ZCA白化算法,并描述如何使用高效的线性代数库来实现它们。
首先,我们需要确保数据的均值(近似)为零。对于自然图像,我们通过减去每个图像块(patch)的均值(近似地)来达到这一目标。为此,我们计算每个图像块的均值,并从每个图像块中减去它的均值。(译注:参见PCA一章中“对图像数据应用PCA算法”一节)。Matlab实现如下:
avg = mean(x, 1); % 分别为每个图像块计算像素强度的均值。 x = x - repmat(avg, size(x, 1), 1);
下面,我们要计算 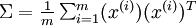 ,如果你在Matlab中实现(或者在C++, Java等中实现,但可以使用高效的线性代数库),直接求和效率很低。不过,我们可以这样一气呵成。
,如果你在Matlab中实现(或者在C++, Java等中实现,但可以使用高效的线性代数库),直接求和效率很低。不过,我们可以这样一气呵成。
sigma = x * x' / size(x, 2);
(自己推导一下看看)这里,我们假设 x 为一数据结构,其中每列表示一个训练样本(所以 x 是一个 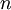 ×
×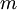 的矩阵)。
的矩阵)。
接下来,PCA计算 Σ 的特征向量。你可以使用Matlab的 eig 函数来计算。但是由于 Σ 是对称半正定的矩阵,用 svd 函数在数值计算上更加稳定。
具体来说,如果你使用
[U,S,V] = svd(sigma);
那矩阵 U 将包含 Sigma 的特征向量(一个特征向量一列,从主向量开始排序),矩阵S 对角线上的元素将包含对应的特征值(同样降序排列)。矩阵 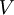 等于
等于 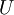 的转置,可以忽略。
的转置,可以忽略。
(注意 svd 函数实际上计算的是一个矩阵的奇异值和奇异向量,就对称半正定矩阵的特殊情况来说,它们对应于特征值和特征向量,这里我们也只关心这一特例。关于奇异向量和特征向量的详细讨论超出了本文范围。)
最后,我们可以这样计 算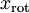 和
和 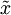 :
:
xRot = U' * x; % 数据旋转后的结果。 xTilde = U(:,1:k)' * x; % 数据降维后的结果,这里k希望保留的特征向量的数目。
这以 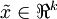 的形式给出了数据的PCA表示。顺便说一下,如果 x 是一个包括所有训练数据的
的形式给出了数据的PCA表示。顺便说一下,如果 x 是一个包括所有训练数据的 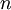 ×
×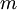 矩阵,这也是一种向量化的实现方式,上面的式子可以让你一次对所有的训练样本计算出 xrot 和
矩阵,这也是一种向量化的实现方式,上面的式子可以让你一次对所有的训练样本计算出 xrot 和 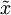 。得到的 xrot 和
。得到的 xrot 和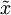 中,每列对应一个训练样本。
中,每列对应一个训练样本。
为计算PCA白化后的数据 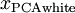 ,可以用
,可以用
xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;
因为 S 的对角线包括了特征值 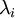 ,这其实就是同时为所有样本
,这其实就是同时为所有样本 计算
计算 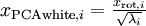 的简洁表达。
的简洁表达。
最后,你也可以这样计算ZCA白化后的数据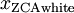 :
:
xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;
原链接:http://deeplearning.stanford.edu/wiki/index.php/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90
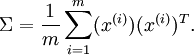
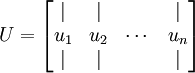
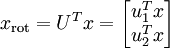
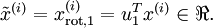
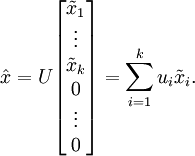
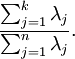
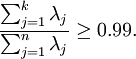
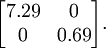
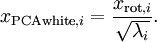
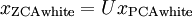
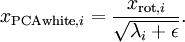










)


![[AlwaysOn Availability Groups] 健康模型 Part 2 ——扩展](http://pic.xiahunao.cn/[AlwaysOn Availability Groups] 健康模型 Part 2 ——扩展)





)