一、选择排序简介

选择排序(Selection sort)是一种简单直观的排序算法。选择排序首先从待排序列表中找到最小(大)的元素，存放到元素列表的起始位置(与起始位置进行交换)，作为已排序序列，第一轮排序完成。然后，继续从未排序序列中找到最小(大)的元素，存放到已排序序列的末尾。直到所有元素都存放到了已排序序列中，列表排序完成。选择排序每次都是去找最小(大)的元素，隐含了一种挑选的过程，所以被称为选择排序。

二、选择排序原理

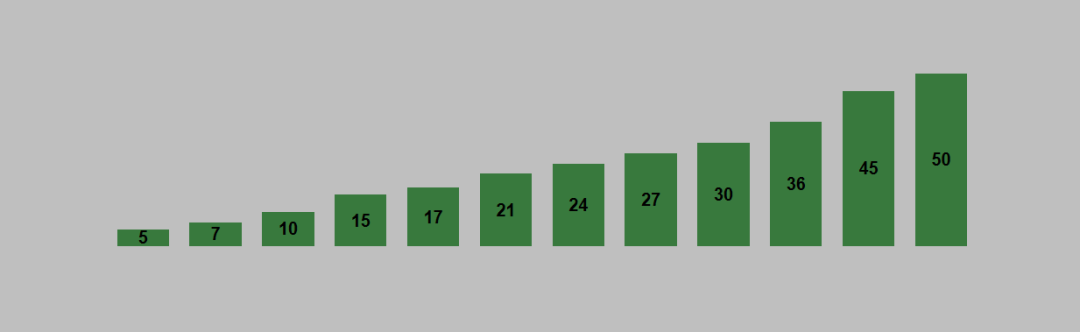
选择排序的原理如下：1. 从待排序列表中找到最小的元素(升序排列，降序排列则找最大的元素)，存放到列表的起始位置，作为已排序的序列。2. 继续从未排序序列中找到最小的元素，存放到已排序序列的末尾(同时也是未排序序列的起始位置)。3. 重复第2步，直到所有元素都已经存放到了已排序序列，则列表排序完成。以列表 [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21] 进行升序排列为例。列表的初始状态如下图。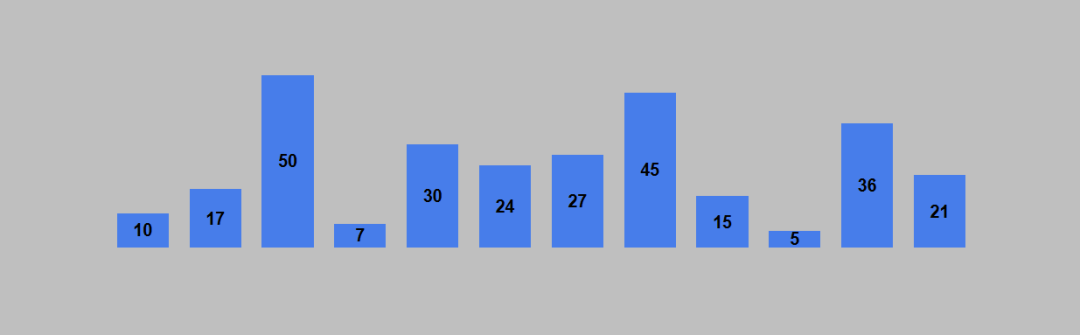

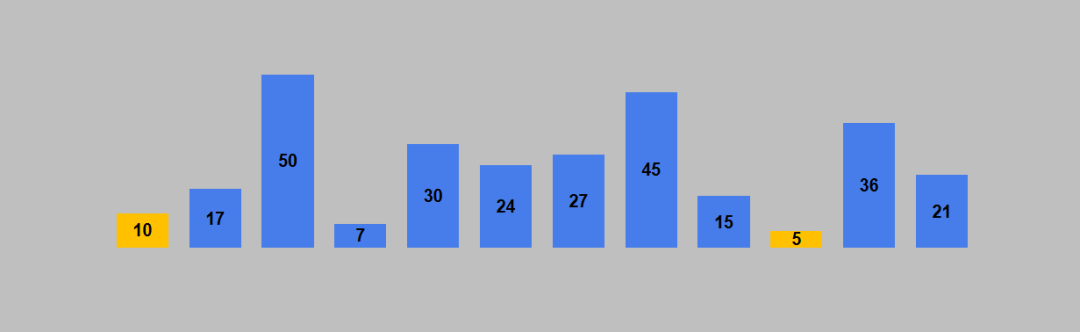
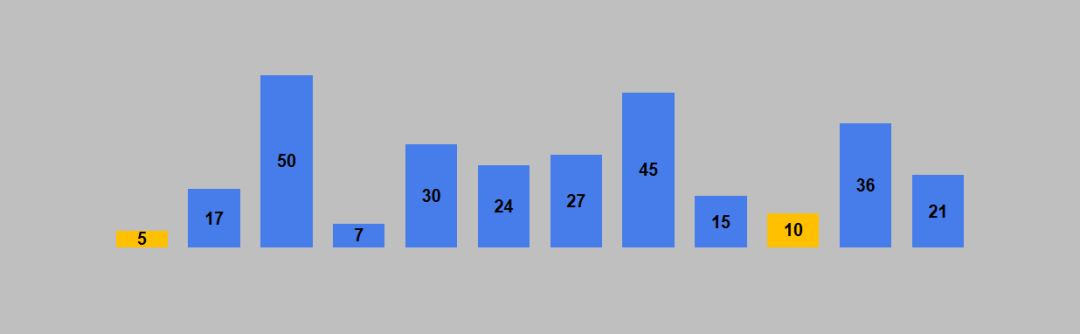
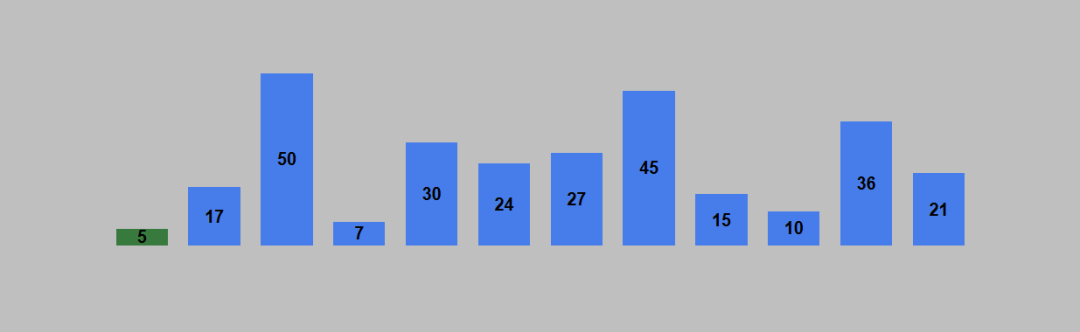
要进行升序排列，则每轮排序都要找到最小的元素。1. 找到元素列表中最小的元素，与列表起始位置的元素进行对比，如果最小的元素小于起始位置的元素，则交换位置。

2. 5小于10，交换位置，将最小的元素存放到列表的起始位置。

3. 将最小的元素作为已排序序列，后面的元素为未排序序列。

4. 继续找到未排序序列中的最小元素，与未排序序列的第一个元素(已排序序列的末尾)比较，如果最小的元素更小则交换位置。

5. 7小于17，交换位置。将最小的元素存放在已排序序列的末尾。

6. 第二轮排序完成后，已排序序列的长度变成二，未排序序列的长度减一。

7. 继续重复上面的4,5步骤，找到未排序序列中的最小元素，存放到已排序序列的末尾。每进行一轮排序，已排序序列的长度加一，未排序序列的长度减一，直到未排序序列的长度为1，列表排序完成。排序结果如下图。

三、Python实现选择排序

# coding=utf-8def selection_sort(array):    for i in range(len(array)-1):        min_index = i        for j in range(i+1, len(array)):            if array[j] < array[min_index]:                min_index = j        if min_index != i:            array[i], array[min_index] = array[min_index], array[i]    return arrayif __name__ == '__main__':    array = [10, 17, 50, 7, 30, 24, 27, 45, 15, 5, 36, 21]    print(selection_sort(array))

运行结果：

[5, 7, 10, 15, 17, 21, 24, 27, 30, 36, 45, 50]

代码中，i 表示第几轮排序，j 表示走访未排序序列中元素的索引，将走访到的每一个元素与未排序序列的第一个元素进行比较。min_index 用于标记当前这一轮排序中最小元素的索引，如果走访到 j 索引的元素比 min_index 索引的元素小，则将 j 赋值给 min_index，j 继续走访。走访完所有元素后，将 min_index 索引的元素交换到 i 索引的位置(未排序序列的起始位置)。

四、选择排序的时间复杂度和稳定性

1. 时间复杂度在选择排序中，不管待排序列表的初始状态如何，都不影响排序的时间复杂度。选择排序需要进行 n-1 轮排序，每一轮排序需要进行 n-i 次比较，i 的平均值是 n/2 ，时间复杂度为 T(n)=n(n-1)/2 ，再乘每次操作的步骤数(常数，不影响大O记法)，所以选择排序的时间复杂度为 O(n^2) 。2. 稳定性在选择排序中，每次都是选择未排序序列中的最小元素，交换到未排序序列的起始位置。存在相等的元素时，如果最小的元素都比它们靠后，最小的元素与相对位置靠前的元素进行交换，则它们的相对位置就发生了变化。如 [10, 10, 5]，进行选择排序后两个 10 的相对位置发生了变化。所以选择排序是一种不稳定的排序算法。