在开始学习PetShop 4.0之前，应首先确认应用程序所需软件环境和自身权限，然后才能够安装。执行安装必须具有系统管理员以及数据库管理的权限。PetShop 4.0要求用户计算机软件环境必须符合以下条件：（1）操作系统为Windows XP SP2或者Windows Server 2003；（2）IE 6.0及其以上版本；（3）Visual Studio 2005；（4）.NET Framework 2.0；（5）SQL Server 2000/2005、SQL Server 2005 Express或者Oracle 10g。当用户确认计算机中已正确安装以上软件后，方可开始安装PetShop 4.0，否则会出现无法安装PetShop 4.0，或者虽然能够安装PetShop 4.0，但是无法正常运行等错误。在本书附带光盘中可以找到PetShop 4.0安装文件，其名称为Microsoft .NET Pet Shop 4.0.msi。另外，也可以从微软网站直接下载该文件，下载地址为：http://download.microsoft.com/download/ 8/0/1/801ff297-aea6-46b9-8e11-810df5df1032/Microsoft% 20.NET%20Pet%20Shop%204.0.msi。双击该文件可以开始PetShop 4.0的安装过程。图18-1所示显示了PetShop 4.0安装过程用户界面。
<!--[if !vml]-->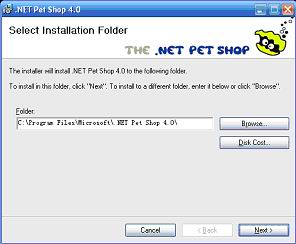
<!--[endif]-->
图18-1 PetShop 4.0安装界面图1
PetShop 4.0的安装过程与安装其他应用程序类似，只要不断单击“下一步”按钮即可。在整个安装过程中，需要注意两个方面：一是PetShop 4.0安装程序允许用户设置源文件存储目录（见图18-1）。默认情况下，源文件存储在C:\Program File\Microsoft\.NET Pet Shop 4.0\。二是安装过程后期将为应用程序设置所安装的数据库类型，此时将显示如图18-2所示的窗口。
<!--[if !vml]-->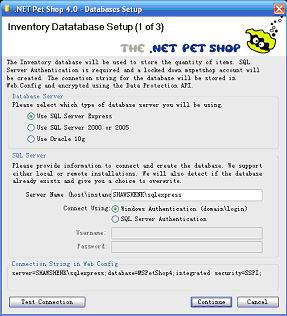
<!--[endif]-->
图18-2 PetShop 4.0安装界面图2
图18-2所示窗口用于设置PetShop 4.0所安装的数据库类型。窗口上半部分用于设置数据库类型，例如，SQL Server、Oracle 10g，下半部分用于设置数据库身份验证方式和显示连接字符串，例如，验证方式、用户名、密码等。选择哪一种数据库类型，则安装程序就在哪种数据库中创建有关PetShop 4.0的数据库实例。当选择了一种数据库类型，并设置相应验证方式后，可通过单击“Test Connection”按钮来检验是否可连接数据库。由于PetShop 4.0主要包括3个数据库实例，因此，窗口也对应设置了3个步骤分别为这些实例定义数据库类型。建议用户统一设置一种数据库类型，而不要将3个数据库实例创建在不同类型的数据库中。例如，选择的数据库类型为SQL Server Express，则安装程序将默认在C:\Program Files\Microsoft SQL Server\MSSQL.1\MSSQL\ Data\中自动生成有关PetShop 4.0的数据库实例文件。
在安装程序结束之后，还必须执行一项操作，才能完整实现PetShop 4.0的安装。即检查操作系统是否启用了DTC（Distributed Transaction Coordinator，分布式事务处理协调器）服务。该服务主要用于协调跨多个数据库、消息队列、文件系统等资源管理器的事务。执行这项操作是由于PetShop 4.0应用程序使用了该服务。单击桌面上“我的电脑”，并选取“管理”选项，然后，在弹出的“计算机管理”窗口中查看系统服务内容。在服务列表中，包括一个Distributed Transaction Coordinator服务。当查看该服务属性时，将弹出如图18-3所示窗口。
<!--[if !vml]-->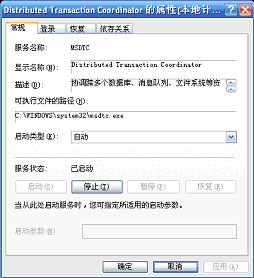
<!--[endif]-->
图18-3 DTC服务设置窗口
默认情况下，DTC服务被设置为手动方式启动。如图18-3所示，必须将该服务的启动类型设置为“自动”。这样，PetShop 4.0就能够随时调用该服务，以便完成应用程序功能。
以上过程完成了PetShop 4.0应用程序的全部安装工作。下面可利用Visual Studio 2005来加载和运行该应用程序，以便了解PetShop 4.0的功能和具体实现过程。
)
 (转))
