【0】README
0.1) source code and text description are from data structure and alg analysis ;
0.2) there are 4 methods solving maximum sum of subsequence, but the fourth proves to be the best one , the 3rd deserves learning for ‘Divide and Conquer’;
0.3) what’s the maximum sum of subsequence ?
Method1)尝试穷举所有可能情况:
源代码: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter2/p18.c
我们由内到外分析上述算法的时间复杂度(Analysis):
- A1)最内层循环
- A2)中间层循环
- A3)最外层循环
代码演示分析步骤:
算法描述(Description):
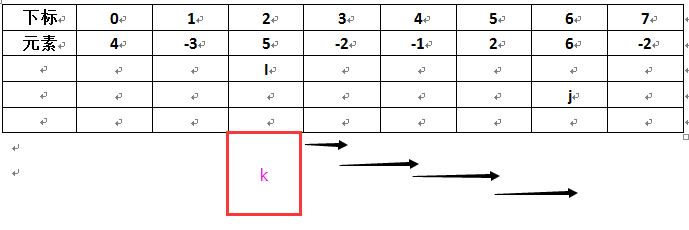
- D1)显然 i, j 分别作为小数组(我暂且这么叫)的下上限(这个上下限通过两个for循环来实现),然后指针k在里面滑动,计算累加和;
- D2)显然算法的最内层循环过分地耗时了。因为之前算了的, 我还要重新算一次。如第一步要计算 A[2] ~ A[5] 的累加和,我第二步还要算 A[2]~A[6] 的累加和,所以说第二步是重复了第一步的大多数工作,因为A[2] ~ A[5]的累加和在第一步已经算过了;
Method2)我们撤除一个for循环来避免立方运行时间:
源代码: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter2/p19.c

时间复杂度分析
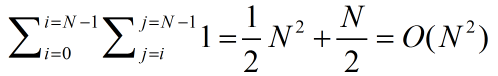
代码演示分析步骤:

算法描述(Description):
- D1)显然 i 作为小数组的上限,下限始终是末尾元素(这个上下限通过两个for循环来实现);
- D2)在小数组中,我们并没有用for循环来遍历所有元素,因为那是无效的,而是用一个if语句来判断是否 在遍历某元素 A[j] 后, sum是增加还是减少,增加,我们就赋值给maxsum, 减少,不赋值就是了,从而撤销掉一个for循环;
Method3)采用分治思想来解决(分治是干货)
源代码: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter2/p20.c

算法描述:其思想是把问题分成两个大致相等的子问题,然后递归地对它们进行求解,这是“分”部分;“治”阶段 将两个子问题的解合并到一起并可能再做些少量的附加工作,最后得到整个问题的解;
- 在我们的例子中(求最大子序列和的问题),最大子序列和可能出现在三个地方——或者整个出现在输入数据的左半部、或者整个出现在右半部、或者跨越输入数据的中部从而占据左右两半部分;
- 如何求其解呢? 前两种情况,可以递归求解,第3中情况的最大和可以通过求出前半部分的最大和(包含前半部分的最后一个元素)以及 后半部分的最大和(包含后半部分的第一个元素)而得到。然后将这两个和加在一起;
考虑以下输入:
- 代码演示分析步骤
算法流程演示
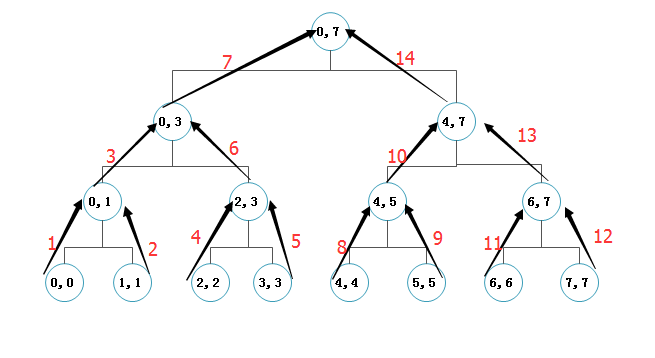
Attention):
- A1)如(0,7)表示(left, right), 而center = (left + right) /2
- A2)显然算法把 整个序列分割成若干了子序列,各子序列和进行比较,求出序列最大值; 其中最经典的是 max3()函数的调用,它返回的是两个子节点的序列和 和 其最近父节点序列和的最大值。然后回溯回去,一步一步进行(1,2,3... 表示返回的递归回溯的次序)
- A3)这个函数 maxSubSum_3()是如何返回序列的最大和的——主要还是依赖与 max3()函数的存在。
- Attention)看到没有? 该函数的递归次序类似于二叉树的 后序递归 idea(上图中的二叉树)。
Method4)利用联机算法解决最大子序列和问题
源代码: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/blob/master/chapter2/p21.c

时间复杂度:T(N)=O(N)
代码演示步骤

Attention):
- 显然,最大子序列和所在的子序列不包括任意”子子序列“为负的情况,因为负就相当于做减法;当thisSum 小于 0 时,令thisSum=0, 即排除了子序列和为负的情况;
算法解说(Commentary):
- C1)优点: 它只对数据进行一次扫描,一旦A[i]被处理,就不需要再记忆了;
- C2)在任意时刻, 算法都能对他已经读入的数据给出子序列问题的正确答案;
- C3)具有这种特性的算法叫——联机算法(online algorithm);
- C4)仅需要线性时间运行的联机算法几乎是完美的算法;
What’s the online algorithm ?
- 如果在任何时刻,算法都能对它已经读入的数据给出子序列问题的正确答案,具有这种特性的算法叫做 联机算法;
因此如果数组在磁盘或磁带上,它就可以被顺序读入,在主存中不必存储数组的任何部分。所以这个算法是一个几乎完美的 联机算法; - 【百度百科】
在任意时刻算法对要操作的数据只读入(扫描)一次,一旦被读入并处理,它就不需要再 被记忆了。而在此处理过程中算法能对它已经读入的数据立即给出相应子序列问题的正确答案。具有这种特性的算法叫做联机算法(on-line algorithm);
Complementary)分治法 与 动态规划
- C1)分治法: 分治法是将问题分为一系列独立小问题,然后分别找到每个小问题的解决方案,然后把每部分的解决方案合并起来,适用于具有同类解决方案的子问题 的求解;
- C2)动态规划:动态规划是将问题分为一系列 相互联系 的子问题,求解一个子问题可能要用到已经求解过的子问题的解,子问题具有重叠性,适合具有重叠子问题性质的问题求解;


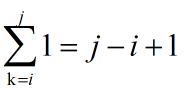
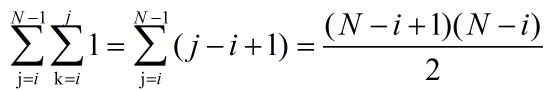
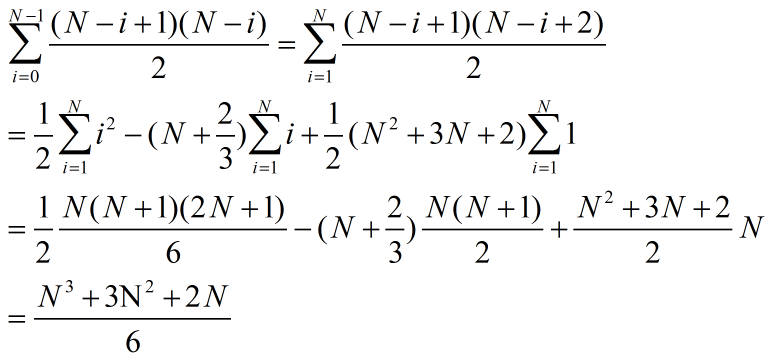















)






