最小生成树——Kruskal（克鲁斯卡尔）算法

【0】README

0.1） 本文总结于数据结构与算法分析，源代码均为原创，旨在理解 Kruskal（克鲁斯卡尔）算法 的idea 并用源代码加以实现；
0.2）最小生成树的基础知识，参见 http://blog.csdn.net/pacosonswjtu/article/details/49947085

【1】 Kruskal 算法（使用到了不相交集ADT的union/find 操作）

1.1）第二种贪婪策略是： 连续地按照最小的权选择边，并且当所选的边不产生圈时就可以吧它作为取定的边；
1.2）形式上， Kruskal算法是在处理一个森林——树的集合。 开始的时候，存在 |V|颗单节点树，而添加一边则将两棵树合并成一颗树，当算法终止的时候就只有一棵树了，这颗树就是最小生成树；
1.3）Kruskal算法的执行步骤，如下图所示，看个荔枝：

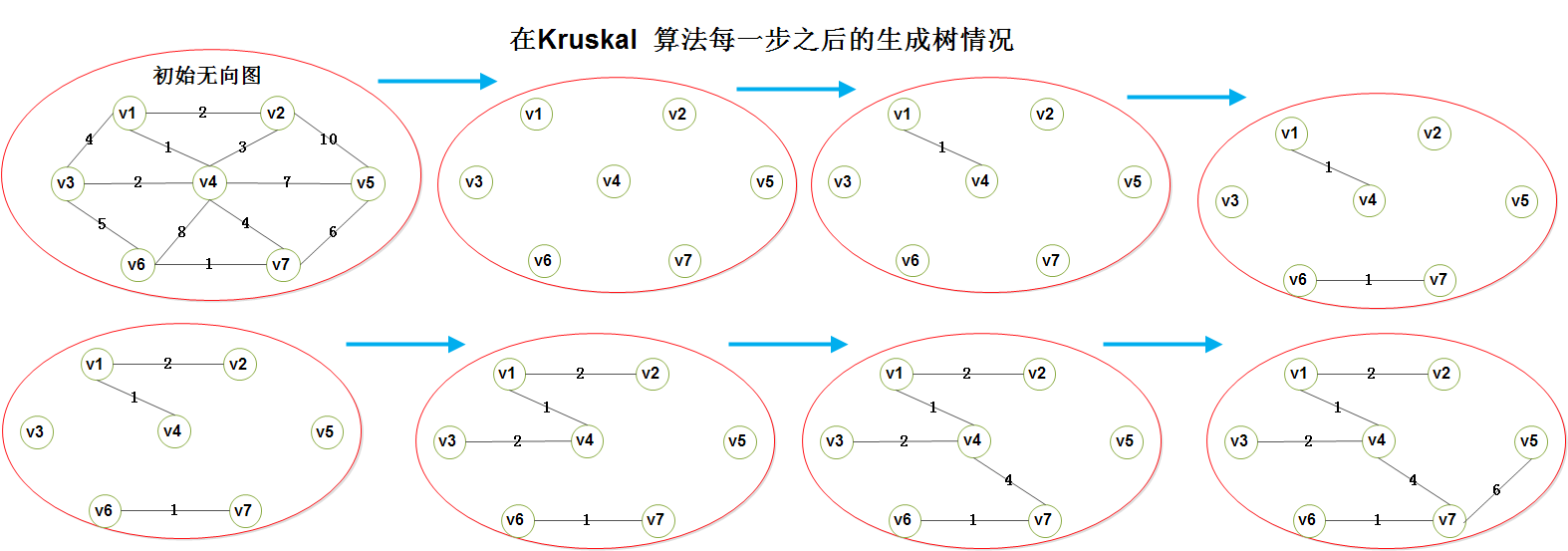
对上图的分析（Analysis）：

A1）当添加到森林中的边足够多时算法终止，实际上，算法就是要决定边（u, v）应该添加还是放弃。（前一章节中的 Union/Find 算法在这里适用）

1.4）我们用到了一个恒定的事实：在算法实施的任意时刻，两个顶点属于同一个集合当且仅当它们在当前的森林中连通；因此，每个顶点最初是在它自己的集合中；

1.4.1） 如果u 和 v 在同一个集合中，那么连接它们的边就要放弃，因为由于它们已经连通了，如果再添加一条边（u, v）就会形成一个圈了。
1.4.2）如果这两个顶点不在同一个集合中，则将该边加入，并对包含顶点u 和 v 的这两个集合实施一次合并。
1.4.3）容易看到，这样将保持集合不变性，因为一旦边（u, v）添加到生成森林中，若w连通到 u 而 x连通到v，则x 和 w 必然是连通的，因此属于相同集合；

1.5）固然，将边排序可便于选取，不过，用线性时间建立一个堆则是更好的想法；

1.5.1）此时， deleteMin 将使得边依序得到测试。 典型情况下，在算法终止前只有一小部分边需要测试，尽管测试所有的边的情况是有可能的；例如，还有一个顶点 v8以及值为100的边（v5, v8），那么所有的边都会要考察到；

1.6）因为一条边由3个部分的数据组成，所以在某些机器上吧优先队列实现成指向边的指针数组比实现成边的数组更为有效。

1.6.1）这种实现的效果在于，为重新排列堆，需要移动的只有那些指针，而大量的记录则不必移动；

1.7）时间复杂度：该算法的最坏情形运行时间为 O（|E|log|E|），它受堆操作控制。注意，由于 |E|=O(|V|^2)，因此这个运行时间实际上是 O（|E|log|V|）。在实践中，该算法要比这个时间界指示的时间快得多；

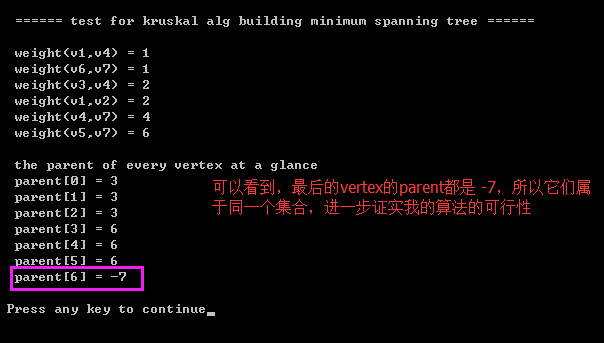
【2】source code + printing results（将我的代码打印结果同 “1.3” 上图中的手动模拟的 Kruskal 算法的结果进行比较，你会发现，它们的结果完全相同，这也证实了我的代码的可行性）

2.0）code specification：

s1）本代码采用了优先队列（二叉小根堆）来升序选取边；
s2）本代码采用了用到了不相交集ADT的 find和setUion 操作来对边的两个vertexes 进行union 操作以及更新它们的根；
s3）对于根的初始化，我是这样初始化的—— parent[0]=-1,parent[1]=-2, parent[2]=-3, parent 说白了，就是 set的一个 index，所以开始肯定是不一样的；然后，在union的时候，我只要检查是否 i == -parent[i]-1 就可以知道它是否是树的根；
s4）在合并的时候，要对边的两个顶点 start 和 end 的 parent做update，这里涉及到4种情况—— start为根且end不为根；start为根且end为根；start为不为根且end为根；start不为根且end不为根； （干货，本代码的重中之重以及新颖之处）

2.1）download source code： https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/p240_kruskal
2.2）source code at a glance（for complete code , please click the given link above）：

#include <stdio.h>
#include "binaryheap.h"// allocate memory for the vertexes with size
Vertex* makeEmptyVertexes(int size)
{Vertex *array; int i;array = (Vertex*)malloc(size * sizeof(Vertex)); if(!array){Error("out of space, from func makeEmptyVertexes");return NULL;} // initializing the set index towards every vertex with its array indexfor(i = 1; i <= size; i++)array[i-1] = -i;return array;
}void printParent(Vertex* vertexes, int size)
{int i;printf("\n\n\t the parent of every vertex at a glance");for(i=0; i<size; i++)printf("\n\t parent[%d] = %d", i, vertexes[i]);
}int find(Vertex *parent, Vertex single){while (single >= 0)single = parent[single]; return single;
}//judge whether the vertex index is the parent or not, also 1 or 0
//if the vertex under index is not the parent ,that's to say its parent is one of other vertexes
int isParent(Vertex *parent, Vertex index)
{return parent[index] == -index-1;
}void setUnion(Vertex *parent, Vertex start, Vertex end)
{   if(isParent(parent, start) ) // start is the parent {if(!isParent(parent, end)) // but end is not the parentend = find(parent, end) + 1; // find the parent of endparent[start] = end;        }else // start is not the parent {start = -find(parent, start) - 1; // find the parent of startif(!isParent(parent, end)) // but end is not the parentend = find(parent, end) + 1; // find the parent of endparent[end] = start;}
}void kruskal(BinaryHeap bh, int vertexNum)
{int counter;int set1;int set2; Vertex start;Vertex end;Vertex* parent;ElementType singleEdge; counter = 0;    parent = makeEmptyVertexes(vertexNum);while(counter < vertexNum - 1){singleEdge = deleteMin(bh);start = singleEdge.start;end = singleEdge.end;set1 = find(parent, start);set2 = find(parent, end);// find the set of vertex start and endif(set1 != set2){               setUnion(parent, start, end);counter++;printf("\n\t weight(v%d,v%d) = %d", singleEdge.start+1, singleEdge.end+1, singleEdge.weight);}       }printParent(parent, vertexNum);printf("\n\n\t");
}int main()
{  BinaryHeap bh;ElementTypePtr temp;    int vertexNum;int size = 7;int capacity;int i;int j;  int adjTable[7][7] = {{0, 2, 4, 1, 0, 0, 0},{2, 0, 0, 3, 10, 0, 0},{4, 0, 0, 2, 0, 5, 0},{1, 3, 2, 0, 7, 8, 4},{0, 10, 0, 7, 0, 0, 6},{0, 0, 5, 8, 0, 0, 1},{0, 0, 0, 4, 6, 1, 0},};  vertexNum = 7;capacity = vertexNum * vertexNum;bh = initBinaryHeap(capacity);temp = makeEmptyElement();printf("\n\n\t ====== test for kruskal alg building minimum spanning tree ======\n");//building binary heap with edge including 2 vertexs and its weight for(i = 0; i < size; i++){for(j = i+1; j < size; j++) if(adjTable[i][j]) {               temp->start = i;temp->end = j;temp->weight = adjTable[i][j];              insertHeap(temp, bh); // insertAdj the adjoining table over}}kruskal(bh, vertexNum);return 0;
} // allocate memory for the array with size
ElementTypePtr *makeEmptyArray(int size)
{ElementTypePtr *array;int i;array = (ElementTypePtr*)malloc(size * sizeof(ElementTypePtr)); if(!array){Error("out of space, from func makeEmptyArray");return NULL;}for(i=0; i<size; i++)    array[i] = makeEmptyElement();   return array;
}// allocate memory for the single element 
ElementTypePtr makeEmptyElement()
{ElementTypePtr temp;temp = (ElementTypePtr)malloc(sizeof(ElementType));if(!temp){Error("out of space, from func makeEmptyElement!");return NULL;}return temp;
}