【0】README
0.1) 本文总结于 数据结构与算法分析, 源代码均为原创, 旨在 理解 如何对无向图进行深度优先搜索 的idea 并用源代码加以实现;
0.2) 本文还引入了 背向边(定义见下文描述),并用源代码找出了给定图的在 DFS过程中 产生的背向边, 但是要注意 背向边不是深度优先搜索树的边, 该树是由 对给定图进行DFS生成的;
0.3) 通过打印 parent (可以看做是 深度优先搜索树的边), 我们可以大致知晓 深度优先搜索树的大致框架,并结合背向边,我们就可以将 DFS 的全部流程看清楚了;
0.4)背向边的添加操作是比较重要的: 因为后面的DFS应用到 ”双连通性“、”有向图“以及”查找强分支“ 都要用到 背向边;
0.5)深度优先搜索基础内容, 参见: http://blog.csdn.net/pacosonswjtu/article/details/49967175
【1】DFS应用与无向图相关
1.1)DFS应用与测试无向图是否连通:无向图是连通的, 当且仅当从任一节点开始的深度优先搜索访问到每一个节点。因为这项测试应用起来非常容易, 所以我们将假设我们处理的图都是连通的。如果它们不连通,那么我们可以找出所有的连通分支并将我们的算法依次应用于每个分支;
1.2)看个荔枝:
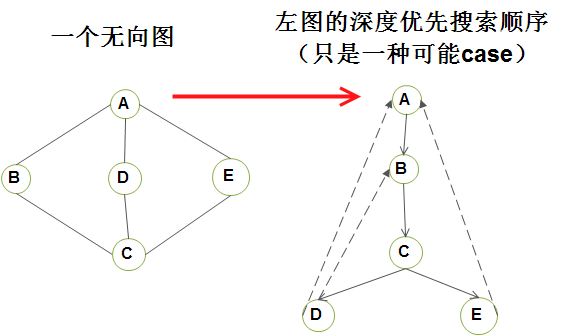
对上图的深度优先搜索步骤(steps)进行分析(Analysis)(这只是深度优先搜索的一种可能情况)
A1)建立深度优先生成树的步骤
- step1)任取一个 顶点A;
- step2)将 顶点A 标记为已访问过, 并递归调用 DFS(B);
- step3)将 顶点B 标记为已访问过, 并递归调用 DFS(C);
- step4)将 顶点C 标记为已访问过, 并递归调用 DFS(D);
- step5)将 顶点D 标记为已访问过, 由于 顶点A,顶点C 均被访问过,所以return;
- step6)递归return到 顶点C, 并递归调用DFS(E);
- step7)将 顶点E 标记为已访问过, 由于没有未被访问过的顶点,所以算法over;
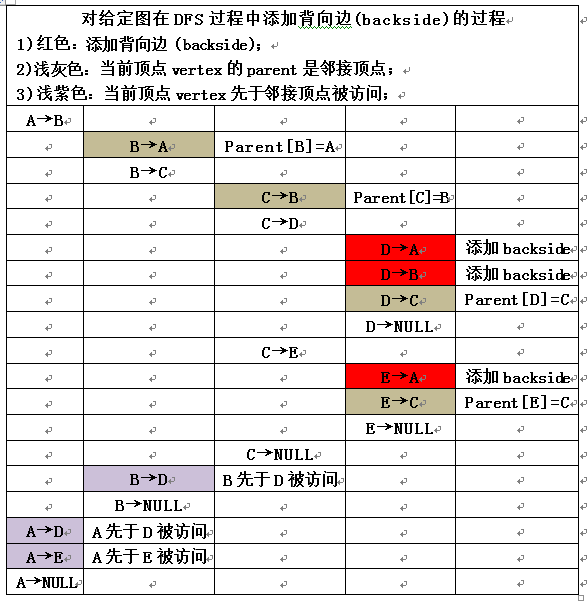
A2)对边的处理(引入背向边的定义): 如果当我们处理(v, w)时 发现w是未被标记的, 或当我们处理(w, v)时发现v是未标记的,那么我们就用树的一条边表示它; 如果当我们处理 (v, w)时发现w 是已被标记的, 并且当我们处理(w, v)时发现v 也是已标记的, 那么我们就画一条虚线, 并称之为背向边,表示这条边实际上不是树的一部分;
1.3)树将模拟我们执行的遍历顺序, 如右上图所示。只使用树的边对该树的先序编号告诉我们这些顶点被标记的顺序。 如果图不是连通的, 那么处理所有节点(和边)都需要多次调用DFS, 每次都生成一颗树,整个集合就是 深度优先生成森林(depth-first spanning forest)如右上图所示;
1.4)深度优先搜索无向图的递归步骤解析如下:
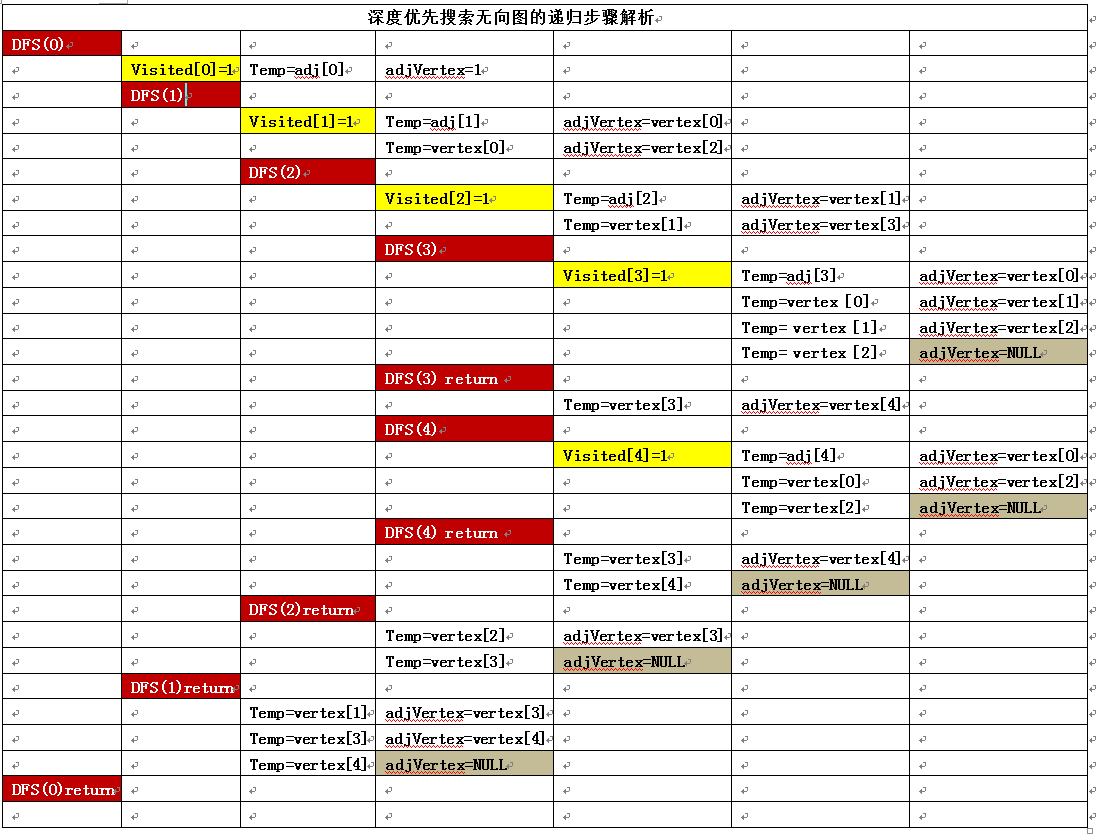 |
1.5)看个荔枝——对给定图在DFS过程中添加背向边(backside)的过程
【2】source code + printing results
2.0)code specification:
我个人以为代码中的干货,一个当然是 DFS 的递归过程,另一个则是 添加背向边的代码,它的if 条件语句如下:
if(visited[adjVertex]) // judge whether the adjVertes was visited before {if(vertexIndex[vertex] > vertexIndex[adjVertex] && parent[vertex] != adjVertex) {//parent[adjVertex] = vertex; // building back side, attention of condition of building back side above// just for printing effectfor(i = 0; i < depth; i++) printf(" ");printf("vertex[%c]->vertex[%c] (backside) \n", flag[vertex], flag[adjVertex]);}}- s1)对以上代码的分析: 当顶点vertex 的邻接顶点被访问过时,如果该邻接顶点 晚于 当前顶点vertex 访问, 且 该邻接顶点不是当前顶点vertex的 parent的话,那么就符合添加 背向边的条件了;(这里有点打脑筋,慢慢理解)
- s2)我们讲为什么要添加背向边? 因为我们的初衷是要让 深度优先搜索树的各个顶点的可达程度 和 给定的初始图的顶点可达情况类似或相同;你要想, 如果存在 (v1,v2) ,那必然有(v2,v1), 所以如果v1 是v2的parent,此时如果你又添加了 v2到 v1的背向边,那岂不是没有意义;我们再想, 如果 v1先于v2被访问, 你又添加了 v1到v2的背向边,那岂不是还是没有意义,请对照到上述代码中的 if 条件语句以便理解 为什么那样去添加背向边;
2.1)download source code: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter9/p241_dfs_undirected_graph
2.2)source code at a glance:(for complete code , please click the given link above)
#include "dfs.h"extern char flag[];void dfs(Vertex vertex, int depth)
{int i;AdjTable temp;Vertex adjVertex; //printf("\n\t visited[%c] = 1 ", flag[vertex]);visited[vertex] = 1; // update visited status of vertexvertexIndex[vertex] = counter++; // number the vertex with countertemp = adj[vertex]; while(temp->next){adjVertex = temp->next->vertex; if(visited[adjVertex]) // judge whether the adjVertes was visited before {if(vertexIndex[vertex] > vertexIndex[adjVertex] && parent[vertex] != adjVertex) {//parent[adjVertex] = vertex; // building back side, attention of condition of building back side above// just for printing effectfor(i = 0; i < depth; i++) printf(" ");printf("vertex[%c]->vertex[%c] (backside) \n", flag[vertex], flag[adjVertex]);}}else{parent[adjVertex] = vertex;// just for printing effectfor(i = 0; i < depth; i++) printf(" ");printf("vertex[%c]->vertex[%c] (building edge)\n", flag[vertex], flag[adjVertex]); dfs(adjVertex, depth+1);}temp = temp->next;}
}
2.3)printing results:
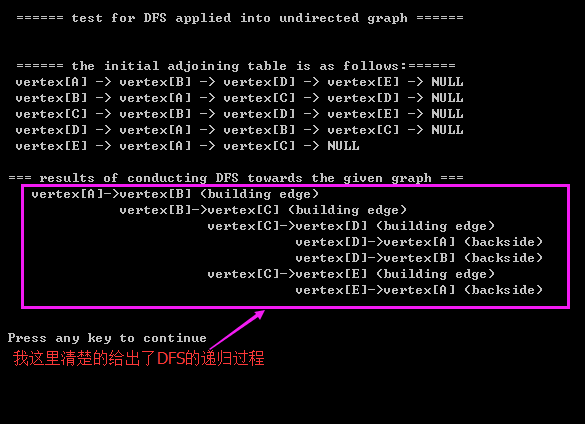
)



之Redis、Jmeter、MySQL的那些事...)








、发送给多人、抄送给多人的示例...)




)
