参考《常微分方程》第三版(王高雄)
常微分方程王高雄 第四章 高阶微分方程_哔哩哔哩 (゜-゜)つロ 干杯~-bilibiliwww.bilibili.com
对于高阶微分方程,线性部分见4、5章,非线性部分见6章。
4.1 线性微分方程的一般理论
定义:线性微分方程分为非齐次微分方程和齐次微分方程
n阶非齐次微分方程:
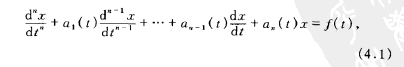
n阶齐次微分方程:
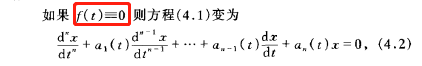
其中系数及f(t)为闭区间[a,b]上的连续函数。
一.首先引进一些本章常用到的定义:
1.朗斯基行列式(p122)

2.函数的线性相关&线性无关

3.基本解组(p126)

二.齐次线性方程基本性质
a)存在唯一性定理

b)叠加原理

c) 函数线性相关性与朗斯基行列式的关系

d)方程解(函数)线性无关,则朗斯基行列式在区间上的任何一点都不为0

根据定理3和定理4可以知道,由n阶齐次线性微分方程(4.2)的n个解构成的朗斯基行列式或者恒等于零,或者在方程的系数为连续的区间内处处不等于零
e)通解结构定理

三.非齐次线性微分方程的基本性质及常数变易法
a)齐次线性微分方程与非齐次线性微分方程解之间的关系


b)常数变易法
设齐次线性微分方程的基本解组与通解如下:

则根据常数变易原理,可设非齐次线性微分方程的通解为:
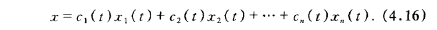
则关键是确定

具体证明及一个例子如下:


例子:

4.2 常系数线性微分方程的解法
事实上,对于一般的线性微分方程是没有普遍的解法的.本节介绍求解问题能够彻底解决的一类方程——常系数线性微分方程及可以化为这一类型的方程.我们将看到,为了求得常系数齐次线性微分方程的通解,只须解一个代数方程而不必通过积分运算.对于某些特殊的非齐次线性微分方程也可以通过代数运算和微分运算求得它的通解,我们一定要记住常系数线性微分方程固有的这种简单特性.
讨论常系数线性微分方程的解法时,需要涉及实变量的复值函数及复指数函数的问题。
4.2.1 复值函数与复值解
一.定义
a)首先给出复值函数的极限、连续、可微的概念

b)

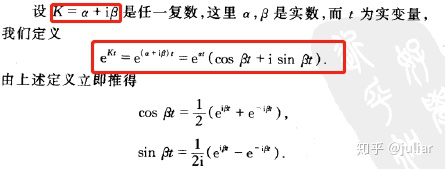
c)
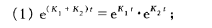
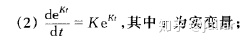
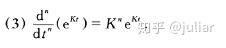
d)方程的复值解的性质

4.2.2 常系数线性微分方程和欧拉方程
一. 齐次线性微分方程
设齐次线性微分方程中所有系数都是常数,即方程有如下形式:

由4.1的一般理论可知,为了求方程(4.19)的通解,只需要求出它的基本解组,求基本解组的一种很重要的方法—欧拉待定指数函数法(特征根法)
(等价转换)分析可知:
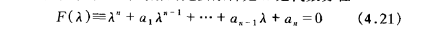
的根。
称(4.21)为(4.19)的特征方程,它的根就称为特征根。对于特征根,下面根据不同的情形分别进行讨论:
(1)单根+实根

方程通解为:
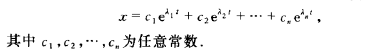
(2)重根+实根(p140)

(4.25)和(4.26)全体n个解构成方程(4.19)的基本解组。对所以基本解组进行系数加权即得到通解。
(3)单根+复根

特征根为
(4)重根+复根(p141):k->2k

二.欧拉方程(p142)
总结:欧拉方程通过自变量变换可转化为常系数齐次线性微分方程,解的求法也类似可以得到

最后可化解为常系数齐次线性微分方程

而由前面的特征根法可知,方程(4.30)有形如
检验:以

下面通过例6进一步理解:

4.2.3非齐次线性微分方程-比较系数法与拉普拉斯变换
前面4.1.3介绍了非齐次线性微分方程求解的常数变易法-即在已知齐次线性微分方程解的前提下,将常数加以自变量约定为非齐次的通解,微分求和,进行化解,求出常数加自变量后的导数,进而确定出常数加自变量的函数形式。。。上述步骤求解往往比较繁琐。下面介绍当f(t)具有某些特殊形状时所适用的一些方法——比较系数法与拉普拉斯变换。它们的特点是不需通过积分而用代数方法即可求得非齐次线性微分方程的特解,即将求解微分方程的问题转化为某一个代数问题来处理,因而比较简便.
1.比较系数法
- 类型I(p145)

- 类型II(p148)

- 类型II的特殊情形(p150)

2.拉普拉斯变换(p150)


4.3 高阶微分方程的降阶和幂级数解法
对于n阶微分方程

4.3.1 可降阶的一些方程类型
下面讨论三类特殊方程的降阶问题:
1.方程不显含未知函数(p166)

2.不显含自变量t的方程(p167)

3.齐次线性微分方程

4.3.2 幂级数解法(p173)

更多可参见书中p173
matlab解微分方程:
y- p130例1:
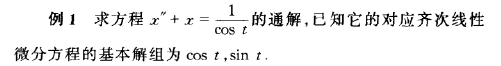
matlab实现:
x=dsolve('D2x+x=1/cos(t)')x =C10*cos(t) + log(cos(t))*cos(t) + C11*sin(t) + t*sin(t)与书中结果一样。
- p130例2:
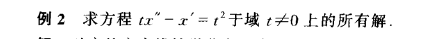
matlab实现:
>> x=dsolve('t*D2x-Dx=t^2')x =C16*t^2 + t^2*(t/3 + C15/(2*t^2))- p154例13
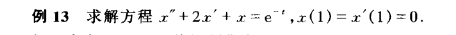
matlab实现:(注意数乘符号*不能省)
x=dsolve('D2x+2*Dx+x=exp(t)','x(1)=Dx(01)=0')x =(t*exp(t))/2 - (exp(t)*(2*t - 1))/4 - (C30*exp(-t))/2 + C30*t*exp(-t)2020.11.19







)











