树学

文章目录

- 题目描述
- 题解1：
- 代码:
- 题解2：
- 代码：

传送

时间限制：C/C++ 2秒，其他语言4秒空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format:> %lld

题目描述

牛妹有一张连通图，由n个点和n-1条边构成，也就是说这是一棵树，牛妹可以任意选择一个点为根，根的深度dep_root为0，对于任意一个非根的点，我们将他到根节点路径上的第一个点称作他的父节点，例如1为根，1-4的；路径为1-3-5-4时，4的父节点是5，并且满足对任意非根节点，dep_i=dep_fa _i+1,整棵树的价值W=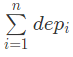 在这里插入图片描述，即所有点的深度和

牛妹希望这棵树的W最小，请你告诉她，选择哪个点可以使W最小
输入描述:
第一行，一个数，n
接下来n-1行，每行两个数x,y，代表x-y是树上的一条边
输出描述:
一行，一个数，最小的W
示例1
输入

输出

备注:
对于30%30%的数据，1<= n<=1000
对于100%100%的数据，1<=n <=10⁶

题解1：

树形dp+换根
用到的几个函数：
dep[i]：节点i的深度
ant[i]：i的子树的个数（含本身）
f[x]：以x为根的每个节点深度的和
在这里插入图片描述
图一为以u为根节点
图二为以v为根节点
从u转到v 之后，图二中黄色区域（u和子树1和子树2）根节点都加1（因为成为别人的子节点），绿色区域（v和根节点2）根节点减1（因为成为别人的根节点）
那转换成公式是什么样的？
f[v]=（f[u]-ant[v]）+(n-ant[v]);
怎么理解呢？
第一个括号里，是将图二的绿色区域根节点减一，因为黄色区域一共ant[v]个节点，这个区域内每个节点都减1，所以整个区域f[u]要减ant[v].
第二个括号就是黄色区域每个节点都加一，那整个区域就加这个区域的节点数，这个区域的节点数=整个区域-绿色区域，所以就是n-ant[v]
我们从1开始dfs，求出每个节点的深度，即dep[]
然后再dfs求出每个点子树数量,再dfs换成其他根，利用公式求出f来

代码:

#include<bits/stdc++.h>
#define forr(n) for(int i=1;i<=n;i++)
typedef long long ll;
using namespace std;
const int maxn=1e6+3;
struct node{int u,v,w,next;
}edge[maxn<<1];//链式前项星 
ll head[maxn<<1];//无向边，所以乘2
ll dep[maxn];//节点的深度 
ll ant[maxn];//节点x的子树数量（包含本身） 
ll f[maxn];//以i为根的时候每个点深度的和 
ll cnt=0;
ll minn=1e7;ll n;
void add(ll u,ll v)
{edge[++cnt].v=v;edge[cnt].next=head[u];head[u]=cnt;}
inline void init(ll n)
{forr(n)f[1]+=dep[i];//在dfs1求完每个点深度后，接着求出以1为根的时候每个点深度的和  forr(n)ant[i]=1;//每个节点的子树一开始都是本身 
}	
ll v=0;
void dfs1(ll now,ll fa)
{for(ll i=head[now];i;i=edge[i].next){v=edge[i].v;if(v==fa)continue;dep[v]=dep[now]+1;dfs1(v,now);}
}//以1为根节点开始，计算出每个节点的深度 void dfs2(ll now,ll fa)
{for(ll i=head[now];i;i=edge[i].next){v=edge[i].v;if(v==fa)continue;dfs2(v,now);ant[now]+=ant[v]; }
}//求出x节点的子树数量 
void dfs3(ll now,ll fa)
{for(ll i=head[now];i;i=edge[i].next){v=edge[i].v;if(v==fa)continue;f[v]=f[now]-ant[v]+(n-ant[v]); dfs3(v,now);}
}
//从1开始换成其他根，并求出其他根的f值 
int main()
{cin>>n;for(int i=1;i<n;i++){int u,v;cin>>u>>v;add(u,v);add(v,u);}	dfs1(1,0);init(n);//初始化 dfs2(1,0);dfs3(1,0);forr(n){minn=min(minn,f[i]);} cout<<minn;return 0;}

仔细看会发现dfs1与dfs2结构相似，完全可以和在一起写
或者用vector写更简洁

题解2：

我看有很多大佬都用重心的性质来做
树的重心有一个这样的性质：在树中所有点到某点的距离和当中，到树的重心的距离和是最小的，如果有多个重心，那他们距离和一样。
树中所有点到重心的距离和最小，不就是我们要求的那个值吗。
先用dfs树形dp求出重心，再求出重心与每个点的距离进行累加求和

代码：

#include<bits/stdc++.h> 
using namespace std;typedef long long ll;
const int maxn=1e6+3;
int ant[maxn],root[maxn];
int n,cnt;
ll res;
ll point=maxn;vector<int>edge[maxn];
void dfs1(int v,int p)
{ant[v]=0;int maxx=0;for(int i=0;i<edge[v].size();i++){int u=edge[v][i];if(u!=p){dfs1(u,v);ant[v]+=(ant[u]+1);maxx=max(ant[u],maxx);}}maxx=max(n-ant[v]-1,maxx);if(maxx<point){cnt=0;root[++cnt]=v;point=maxx;}else if(maxx==point)root[++cnt]=v;
}
void dfs2(int v,int p,int dep)
{res+=dep;for(int i=0;i<edge[v].size();i++){int u=edge[v][i];if(u!=p)dfs2(u,v,dep+1);}
}
int main()
{scanf("%d",&n);int u,v;for(int i=1;i<n;i++){cin>>u>>v;edge[u].push_back(v);edge[v].push_back(u);}dfs1(1,0);dfs2(root[1],0,0);printf("%lld\n",res);return 0;
}