Ocelot简易教程（四）之请求聚合以及服务发现

上篇文章给大家讲解了Ocelot的一些特性并对路由进行了详细的介绍，今天呢就大家一起来学习下Ocelot的请求聚合以及服务发现功能。希望能对大家有所帮助。

作者：依乐祝
原文地址：https://www.cnblogs.com/yilezhu/p/9695639.html

请求聚合

Ocelot允许你声明聚合路由，这样你可以把多个正常的ReRoutes打包并映射到一个对象来对客户端的请求进行响应。比如，你请求订单信息，订单中又包含商品信息，这里就设计到两个微服务，一个是商品服务，一个是订单服务。如果不运用聚合路由的话，对于一个订单信息，客户端可能需要请求两次服务端。实际上这会造成服务端额外的开销。这时候有了聚合路由后，你只需要请求一次聚合路由，然后聚合路由会合并订单跟商品的结果都一个对象中，并把这个对象响应给客户端。使用Ocelot的此特性可以让你很容易的实现前后端分离的架构。
为了实现Ocelot的请求功能，你需要在ocelot.json中进行如下的配置。这里我们指定了了两个正常的ReRoutes,然后给每个ReRoute设置一个Key属性。最后我们再Aggregates节点中的ReRouteKeys属性中加入我们刚刚指定的两个Key从而组成了两个ReRoutes的聚合。当然我们还需要设置UpstreamPathTemplate匹配上游的用户请求，它的工作方式与正常的ReRoute类似。

注意：不要把Aggregates中UpstreamPathTemplate设置的跟ReRoutes中的UpstreamPathTemplate设置成一样。

下面我们先上个实例例子先！演示代码已经同步更新Github上。有兴趣的朋友可以查看源码：https://github.com/yilezhu/OcelotDemo

在开始实例前先把我们的ocelot Nuget包升级到最新的12.0.0版本，当然你也可以不进行升级。这里需要注意一下，如果你升级到12.0.0的版本的话，那么你config.AddOcelot()的用法会发生改变，需要传入参数config.AddOcelot(hostingContext.HostingEnvironment)

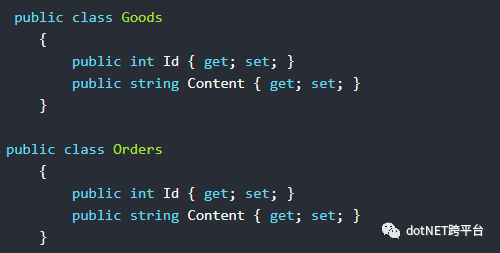
1.为了演示的需要这里我们新增一个类库项目，分别新建两个类，一个是商品Good类，一个是订单Order类（这里只是为了演示的需要，所以代码很简陋）如下所示：

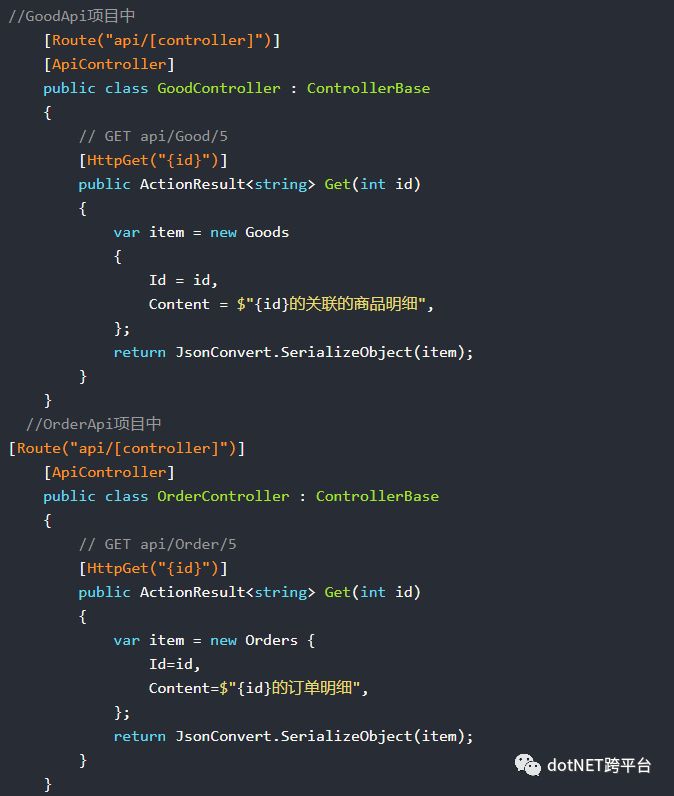
640?wx_fmt=png

接下来我们给OrderApi以及GoodApi分别新建一个控制器，并返回相应的实体。如下所示：

640?wx_fmt=png

接下来我们分别在ocelot.good.json以及ocelot.order.json中新增一个路由，并给出Keys.如下所示：

这里注意，跟上篇文章中的路由不同的是，这里多了一个Key属性。
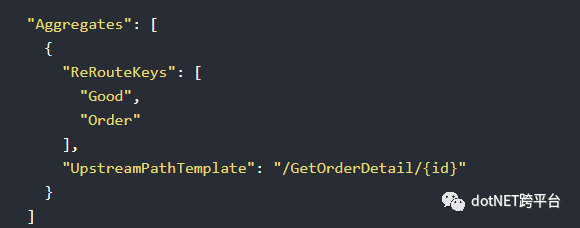
在ocelot.all.json中加入聚合配置，如下所示：
注意：这里Aggregates跟ReRoutes同级，ReRouteKeys中填写的数组就是上面步骤3中设置的Key属性对应的值。
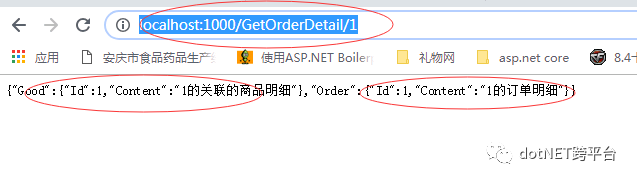
我们分别运行起来三个项目，然后访问接口地址：http://localhost:1000/GetOrderDetail/1 会得到如下的聚合响应内容：

格式化后代码如下：
眼尖的朋友可能已经猜到了。聚合路由返回的内容就是json串。json串由ReRouteKeys组成，每个Key的内容就是具体下游响应的内容了！实例代码已经同步更新到Github上，地址：https://github.com/yilezhu/OcelotDemo
Ocelot将始终使用聚合请求返回内容类型application/json。还有需要注意的是聚合请求不会返回404请求。如果两个下游都返回404状态码的话，这里聚合后的响应也不会返回404，只会返回空的json串，拿上面的实例，如果两个下游都返回404的话，那么他的响应代码类似下面这样：
{   "Good": ,   "Order":
}
如果下游服务返回404，则聚合将仅为该下游服务返回任何内容。即使所有下游都返回404，它也不会将聚合响应更改为404。
服务发现
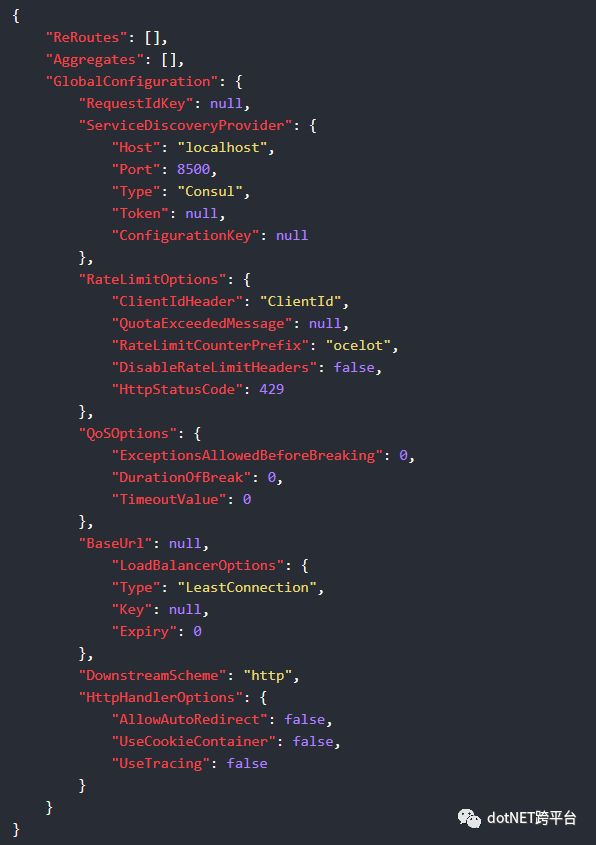
Ocelot允许您指定服务发现提供程序，并将使用它来查找Ocelot将请求转发到的下游服务的主机和端口。目前，这仅在GlobalConfiguration部分中受支持，这意味着相同的服务发现提供程序将用于为ReRoute级别指定ServiceName的所有ReRoutes。
Consul
在使用Consul前你首先要做的就是安装在Ocelot中提供Consul支持的NuGet包
Install-Package Ocelot.Provider.Consul
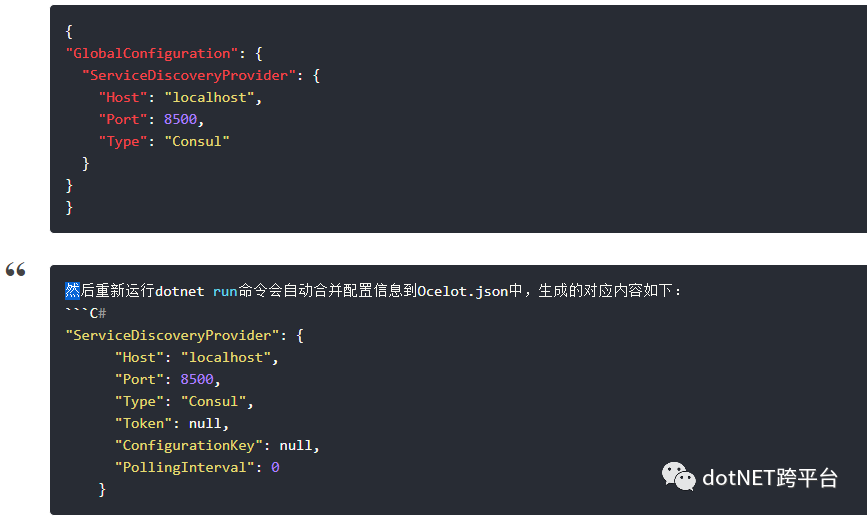
然后将下面的内容添加在ConfigureServices方法中
services.AddOcelot()//注入Ocelot服务.AddConsul(); 
GlobalConfiguration中需要加入以下内容。如果您未指定主机和端口，则将使用Consul默认值。
注意：如果你采用AddOcelot()这种方式来自动加载ocelot配置文件的方式，那么你需要新建一个ocelot.global.json文件，然后加入上面的配置：如下所示：
这个上篇文章中已经进行了相关的介绍。
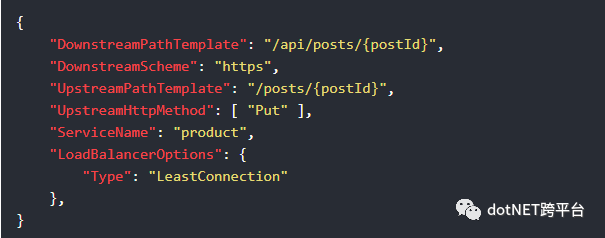
为了告诉Ocelot ReRoute是为其主机和端口使用服务发现提供程序，您必须在下游请求时添加要使用的ServiceName和负载均衡器。目前，Ocelot可以使用RoundRobin和LeastConnection算法。如果未指定负载均衡器，则Ocelot将不会对请求进行负载均衡。
设置此项后，Ocelot将从服务发现提供程序中查找下游主机和端口，并跨任何可用服务进行负载平衡请求。
动态路由
作者的想法是在使用服务发现提供程序时启用动态路由。在此模式下，Ocelot将使用上游路径的第一个段来与服务发现提供程序一起查找下游服务。
例如，使用https://api.yilezhu.cn/product/products 等网址调用ocelot 。Ocelot将采用产品路径的第一部分product，并将其用作在Consul中查找服务的Key。如果consul返回一个服务，Ocelot将使用从consul返回的主机和端口以及剩余路径段组合后的Url来进行请求的响应。，如：http：// hostfromconsul：portfromconsul/products。Ocelot将正常向下游URL转发查询字符串。即query
要启用动态路由，您需要在配置中保留0个ReRoutes。目前您无法混合动态和配置ReRoutes。除此之外，您还需要指定上面概述的Service Discovery提供程序详细信息和下游http / https方案作为DownstreamScheme。
除此之外，您还可以设置RateLimitOptions，QoSOptions，LoadBalancerOptions和HttpHandlerOptions，DownstreamScheme（您可能希望在https上调用Ocelot，但可以通过http与私有服务进行通信），这些将应用于所有动态ReRoutes。
配置可能看起来像:
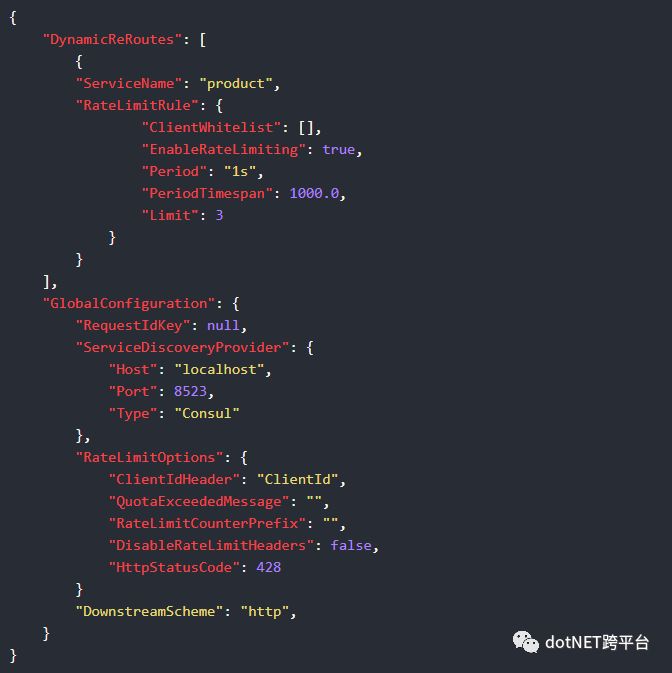
Ocelot还允许您设置DynamicReRoutes，允许您为每个下游服务设置速率限制规则。如果您有一个产品和搜索服务，并且您希望对另一个进行速率限制，则此功能非常有用。这方面的一个例子如下。
此配置意味着如果您在/product/上进入Ocelot请求，则动态路由将启动，并且ocelot将使用针对DynamicReRoutes部分中的产品服务的速率限制设置。
GitHub地址
https://github.com/yilezhu/OcelotDemo
总结
本文接着上篇文章进行了Ocelot请求聚合功能以及服务发现功能的介绍，并且对Ocelot动态路由功能也进行了简单的阐述。对于请求聚合这块进行了相关实例代码的演示，并已经更新到Github上面了！希望能对大家有所帮助！
相关文章：
AspNetCore中使用Ocelot之 IdentityServer4
Ocelot-基于.NET Core的开源网关实现
.NET Core微服务之基于Ocelot+IdentityServer实现统一验证与授权
Swagger如何访问Ocelot中带权限验证的API
Ocelot.JwtAuthorize：一个基于网关的Jwt验证包
.NET Core微服务之基于Ocelot实现API网关服务
.NET Core微服务之基于Ocelot实现API网关服务（续）
.NET微服务体系结构中为什么使用Ocelot实现API网关
Ocelot简易教程（一）之Ocelot是什么
Ocelot简易教程（二）之快速开始1
Ocelot简易教程（二）之快速开始2
Ocelot简易教程（三）之主要特性及路由详解
原文地址: https://www.cnblogs.com/yilezhu/p/9664977.html
.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com