diff 算法

没有 key 时的diff

• 根据新旧列表的长度进行 diff
  • 公共长度相同的部分直接patch
  • 新列表长度>旧列表长度则添加，否则删除

function patchChildren(prevChildFlags,nextChildFlags,prevChildren,nextChildren,container
) {switch (prevChildFlags) {// 省略...// 旧的 children 中有多个子节点default:switch (nextChildFlags) {case ChildrenFlags.SINGLE_VNODE:// 省略...case ChildrenFlags.NO_CHILDREN:// 省略...default:// 新的 children 中有多个子节点// 获取公共长度，取新旧 children 长度较小的那一个const prevLen = prevChildren.lengthconst nextLen = nextChildren.lengthconst commonLength = prevLen > nextLen ? nextLen : prevLenfor (let i = 0; i < commonLength; i++) {patch(prevChildren[i], nextChildren[i], container)}// 如果 nextLen > prevLen，将多出来的元素添加if (nextLen > prevLen) {for (let i = commonLength; i < nextLen; i++) {mount(nextChildren[i], container)}} else if (prevLen > nextLen) {// 如果 prevLen > nextLen，将多出来的元素移除for (let i = commonLength; i < prevLen; i++) {container.removeChild(prevChildren[i].el)}}break}break}
}

通过 key 的 diff

• 通过 key 就能够明确的知道新旧 children 中节点的映射关系，复用旧节点进行 patch

// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {const nextVNode = nextChildren[i]let j = 0// 遍历旧的 childrenfor (j; j < prevChildren.length; j++) {const prevVNode = prevChildren[j]// 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新之if (nextVNode.key === prevVNode.key) {patch(prevVNode, nextVNode, container)break // 这里需要 break}}
}

查找需要移动的节点

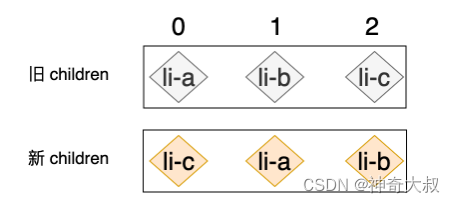
• 如果在寻找的过程中遇到的节点索引呈现递增趋势，则说明新旧 children 中节点顺序相同，不需要移动操作。相反的，如果在寻找的过程中遇到的索引值不呈现递增趋势，则说明需要移动操作
• 因为 diff 是在旧真实节点列表上根据新旧虚拟 vnode 列表进行的真实移动，所以为了保证移动旧列表后的相对位置正确，很多时候都通过insertBefore 替换 appendChild
  • 取出新 children 的第一个节点，即 li-c，并尝试在旧 children 中寻找 li-c，结果是我们找到了，并且 li-c 在旧 children 中的索引为 2。
  • 取出新 children 的第二个节点，即 li-a，并尝试在旧 children 中寻找 li-a，也找到了，并且 li-a 在旧 children 中的索引为 0。
  • 递增的趋势被打破了，我们在寻找的过程中先遇到的索引值是 2，接着又遇到了比 2 小的 0，这说明在旧 children 中 li-a 的位置要比 li-c 靠前，但在新的 children 中 li-a 的位置要比 li-c 靠后。这时我们就知道了 li-a 是那个需要被移动的节点，我们接着往下执行
  • 取出新 children 的第三个节点，即 li-b，并尝试在旧 children 中寻找 li-b，同样找到了，并且 li-b 在旧 children 中的索引为 1。
  • 我们发现 1 同样小于 2，这说明在旧 children 中节点 li-b 的位置也要比 li-c 的位置靠前，但在新的 children 中 li-b 的位置要比 li-c 靠后。所以 li-b 也需要被移动。
• 在当前寻找过程中在旧 children 中所遇到的最大索引值。如果在后续寻找的过程中发现存在索引值比最大索引值小的节点，意味着该节点需要被移动。

// 用来存储寻找过程中遇到的最大索引值
let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {const nextVNode = nextChildren[i]let j = 0// 遍历旧的 childrenfor (j; j < prevChildren.length; j++) {const prevVNode = prevChildren[j]// 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新之if (nextVNode.key === prevVNode.key) {patch(prevVNode, nextVNode, container)if (j < lastIndex) {// 需要移动} else {// 更新 lastIndexlastIndex = j}break // 这里需要 break}}
}

移动节点

• 新 children 中的第一个节点是 li-c，它在旧 children 中的索引为 2，由于 li-c 是新 children 中的第一个节点，所以它始终都是不需要移动的，只需要调用 patch 函数更新即可

function patchElement(prevVNode, nextVNode, container) {// 省略...// 拿到 el 元素，注意这时要让 nextVNode.el 也引用该元素const el = (nextVNode.el = prevVNode.el)// 省略...
}

• 接下来是新 children 中的第二个节点 li-a，它在旧 children 中的索引是 0，由于 0 < 2 所以 li-a 是需要移动的节点，通过观察新 children 可知，新 children 中 li-a 节点的前一个节点是 li-c，所以我们的移动方案应该是：把 li-a 节点对应的真实 DOM 移动到 li-c 节点所对应真实 DOM 的后面
• 所以我们的思路应该是想办法拿到 li-c 节点对应真实 DOM 的下一个兄弟节点，并把 li-a 节点所对应真实 DOM 插到该节点的前面

// 用来存储寻找过程中遇到的最大索引值
let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {const nextVNode = nextChildren[i]let j = 0// 遍历旧的 childrenfor (j; j < prevChildren.length; j++) {const prevVNode = prevChildren[j]// 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新之if (nextVNode.key === prevVNode.key) {patch(prevVNode, nextVNode, container)if (j < lastIndex) {// 需要移动// refNode 是为了下面调用 insertBefore 函数准备的// 拿到新节点列表的上一个节点，插到其后面const refNode = nextChildren[i - 1].el.nextSibling// 调用 insertBefore 函数移动 DOMcontainer.insertBefore(prevVNode.el, refNode)} else {// 更新 lastIndexlastIndex = j}break // 这里需要 break}}
}

添加新元素

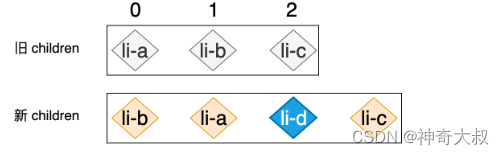
• 节点 li-d 在旧的 children 中是不存在的，所以当我们尝试在旧的 children 中寻找 li-d 节点时，是找不到可复用节点的，这时就没办法通过移动节点来完成更新操作，所以我们应该使用 mount 函数将 li-d 节点作为全新的 VNode 挂载到合适的位置。
• 查找旧节点是否存在 li-d 的 key ，不存在则新增节点
• 如何才能保证 li-d 节点始终被添加到 li-a 节点的后面呢？答案是使用 insertBefore 方法代替 appendChild 方法，因为需要在已存在的真实节点列表进行移动，这样能够保证相对位置正确

let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {const nextVNode = nextChildren[i]let j = 0,find = falsefor (j; j < prevChildren.length; j++) {const prevVNode = prevChildren[j]if (nextVNode.key === prevVNode.key) {find = truepatch(prevVNode, nextVNode, container)if (j < lastIndex) {// 需要移动const refNode = nextChildren[i - 1].el.nextSiblingcontainer.insertBefore(prevVNode.el, refNode)break} else {// 更新 lastIndexlastIndex = j}}}if (!find) {// 挂载新节点// 找到 refNodeconst refNode =i - 1 < 0? prevChildren[0].el: nextChildren[i - 1].el.nextSiblingmount(nextVNode, container, false, refNode)}
}

• 先找到当前遍历到的节点的前一个节点，即 nextChildren[i - 1]，接着找到该节点所对应真实 DOM 的下一个子节点作为 refNode，即 nextChildren[i - 1].el.nextSibling，但是由于当前遍历到的节点有可能是新 children 的第一个节点，这时 i - 1 < 0，这将导致 nextChildren[i - 1] 不存在，所以当 i - 1 < 0 时，我们就知道新的节点是作为第一个节点而存在的，这时我们只需要把新的节点插入到最前面即可，所以我们使用 prevChildren[0].el 作为 refNode

// mount 函数
function mount(vnode, container, isSVG, refNode) {const { flags } = vnodeif (flags & VNodeFlags.ELEMENT) {// 挂载普通标签mountElement(vnode, container, isSVG, refNode)}// 省略...
}// mountElement 函数
function mountElement(vnode, container, isSVG, refNode) {// 省略...refNode ? container.insertBefore(el, refNode) : container.appendChild(el)
}

移除不存在的元素

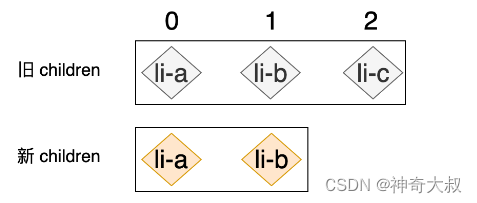
• 新的 children 中已经不存在 li-c 节点了，所以我们应该想办法将 li-c 节点对应的真实 DOM 从容器元素内移除。但我们之前编写的算法还不能完成这个任务，因为外层循环遍历的是新的 children，所以外层循环会执行两次，第一次用于处理 li-a 节点，第二次用于处理 li-b 节点，此时整个算法已经运行结束了。
• 所以，我们需要在外层循环结束之后，再优先遍历一次旧的 children，并尝试拿着旧 children 中的节点去新 children 中寻找相同的节点，如果找不到则说明该节点已经不存在于新 children 中了，这时我们应该将该节点对应的真实 DOM 移除

let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {const nextVNode = nextChildren[i]let j = 0,find = falsefor (j; j < prevChildren.length; j++) {// 省略...}if (!find) {// 挂载新节点// 省略...}
}
// 移除已经不存在的节点
// 遍历旧的节点
for (let i = 0; i < prevChildren.length; i++) {const prevVNode = prevChildren[i]// 拿着旧 VNode 去新 children 中寻找相同的节点const has = nextChildren.find(nextVNode => nextVNode.key === prevVNode.key)if (!has) {// 如果没有找到相同的节点，则移除container.removeChild(prevVNode.el)}
}

缺点

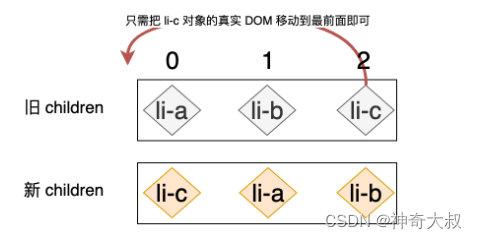
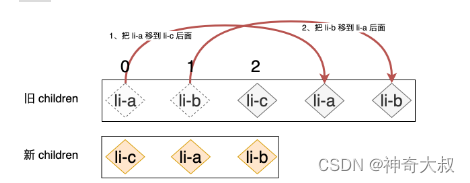
• 在这个例子中，我们可以通过肉眼观察从而得知最优的解决方案应该是：把 li-c 节点对应的真实 DOM 移动到最前面即可，只需要一次移动即可完成更新。然而，React 所采用的 Diff 算法在更新如上案例的时候，会进行两次移动：
  
• 第一次把 li-a 移动到 li-c 后面
• 第二次把 li-b 移动到 li-a 后面