AC自动机，就相当于是在字典树上用kmp。next数组回退的位置为最大匹配字符串在字典树上的节点位置。

在获取字典树上的next数组的时候用的是BFS每次相当与处理的一层。

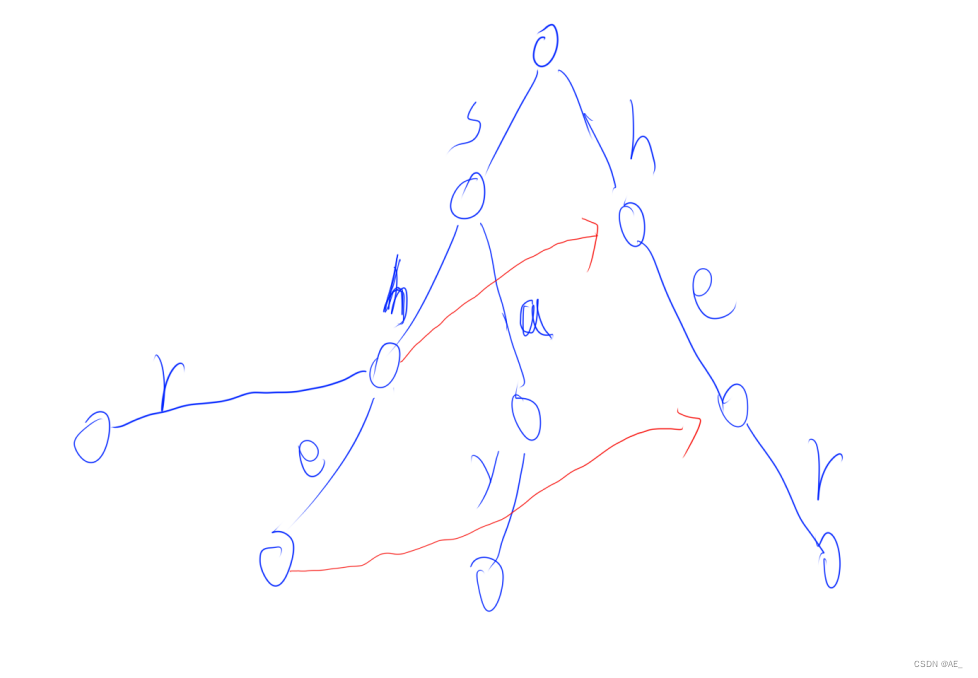
下图中红线为，可以回退的位置，没有红线的节点回退的位置都是虚拟原点。

int n, m;
int o[N];
int tr[N][26], cnt[N], idx;
char str[N];
int q[N], ne[N];inline void insert() { // 正常的字典树插入板子int p = 0;for(int i = 0; str[i]; i ++) {int t = str[i] - 'a';if(!tr[p][t]) tr[p][t] = ++ idx;p = tr[p][t];}cnt[p] ++; // 记录当前字符串出现的次数
}void build() {int  hh = 0, tt = -1;for(int i = 0; i < 26; i ++) // 因为第二层的所有字符串长度为一，next值肯定为1，直接入队即可if(tr[0][i])q[++ tt] = tr[0][i];while(hh <= tt) {int t = q[hh ++];for(int i = 0; i < 26; i ++) {int p = tr[t][i];if(!p) tr[t][i] = tr[ne[t]][i]; // 匹配失败，则回退，路径压缩过，一次回退即可else {ne[p] = tr[ne[t]][i]; // 记录ne数组，顺便压缩路径q[ ++ tt] = p;}}}
}inline void sovle() {idx = 0;cin >> n;for(int i = 0; i < n; i ++) {cin >> str;insert(); // 将所有字符串全都插入字典树}build(); // 获取next数组cin >> str;int res = 0;int s = 0;for(int i = 0, j = 0; str[i]; i ++) { // 同时匹配字典树中所有的字符串int t = str[i] - 'a';j = tr[j][t];int p = j;while(p && cnt[p] != 0) { // 线性匹配，这里的第二个条件是一个优化，只有在每个字符串只记录一次的前提下使用res += cnt[p]; // 记录出现过的字符串的个数cnt[p] = 0; // 因为每个字符串只计算一次，所以要清空p = ne[p]; // 回退}}cout << res << endl;
}

与上一题不一样的只有一小部分，这题中，每个字符串可重复记录，所以就不能加上那个线性优化，还需要记录每个字符串出现的次数即可。

int n, m;
int o[N];
int tr[N][26], cnt[N], idx;
string sr[200];
char str[N];
int q[N], ne[N], st[N];inline void insert(string s) {int p = 0;for(int i = 0; i < s.size(); i ++) {int t = s[i] - 'a';if(!tr[p][t]) tr[p][t] = ++ idx;p = tr[p][t];}cnt[p] ++;
}void build() {int  hh = 0, tt = -1;for(int i = 0; i < 26; i ++)if(tr[0][i])q[++ tt] = tr[0][i];while(hh <= tt) {int t = q[hh ++];for(int i = 0; i < 26; i ++) {int p = tr[t][i];if(!p) tr[t][i] = tr[ne[t]][i];else {ne[p] = tr[ne[t]][i];q[ ++ tt] = p;}}}
}int query(string s) { // 与插入差不多 些许操作不同int p = 0;for(int i = 0; i < s.size(); i ++) {int t = s[i] - 'a';if(!tr[p][t]) return 0;p = tr[p][t];}return st[p];
}inline void sovle() {while(cin >> n, n) {memset(tr, 0, sizeof tr);memset(cnt, 0, sizeof cnt);memset(ne, 0, sizeof ne);memset(st, 0, sizeof st);idx = 0;for(int i = 0; i < n; i ++) {cin >> sr[i];insert(sr[i]);}build();cin >> str;int res = 0;int s = 0;for(int i = 0, j = 0; str[i]; i ++) {int t = str[i] - 'a';j = tr[j][t];int p = j;while(p) {st[p] += cnt[p]; // 记录该字符串出现的次数s = max(st[p], s); // 因为要求出来最多出现的字符串的次数p = ne[p]; // 回退}}cout << s << endl;for(int i = 0; i < n; i ++) {int k = query(sr[i]); // 字典树的查询操作，查询st数组。if(s == k) cout << sr[i] << endl; // 是最大的直接输出。}}
}