我在iOS/Swift工程中成功编译了HarfBuzz！
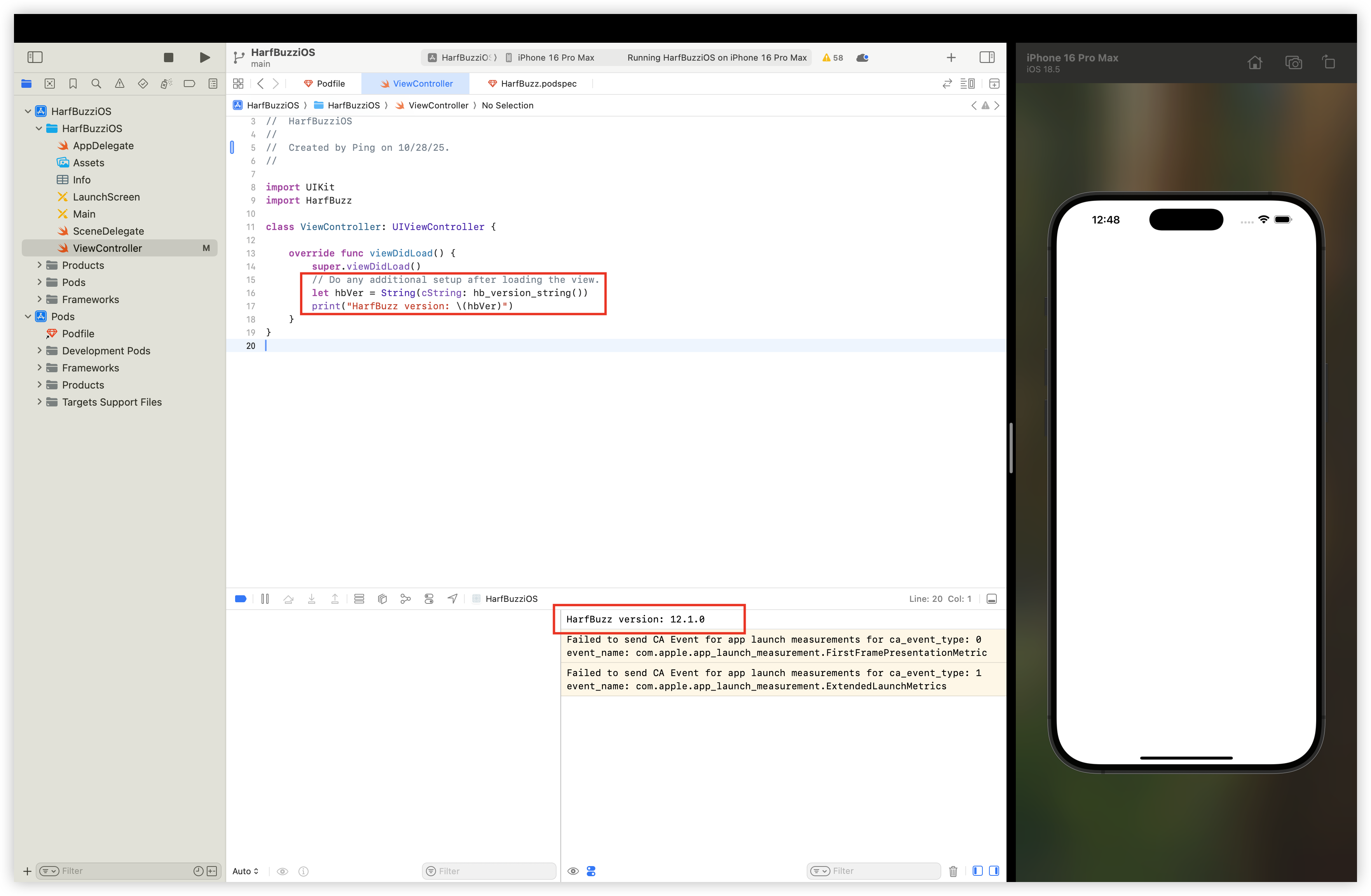
https://github.com/HusterYP/HarfBuzziOS/tree/main
跨端渲染又进一步！！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/949239.shtml
如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
Python access mysql and insert data batch by batch
pip install mysql-connector
or
pip install mysql-connector-python -i https://pypi.tuna.tsinghua.edu.cn/simple/create table t2(id bigint primary key auto_increment,firstname varchar(100) not null defaul…
CodeForces-2153D Not Alone
tag: 结论题，一维线性 DPCodeForces-2153D Not Alone
tag: 结论题，一维线性 DP给定一个环形序列 \(b\)，长度为 \(m\)，每次操作可以将一个数加一或减一。
问最少需要多少次操作，可以使序列 \(b\) 中每一个元素至少…
)
Codeforces Round 1062 (Div. 4)
A. Square?点击查看代码
#include <bits/stdc++.h>using i64 = long long;void solve() {int a, b, c, d;std::cin >> a >> b >> c >> d;if (a == b && b == c && c =…
一文吃透银行账务打通体系闭环 - 智慧园区
银行体系的复杂性，往往源于“账务、账户、会计、科目”之间的模糊边界。本文将系统拆解这四者的逻辑关系，从业务流、资金流到会计流，构建一套可理解、可复用的认知框架，帮助产品人真正打通银行产品设计的底层闭环。…
uups 逻辑合约也增加了升级函数，那总体不是也费gas吗？
这是一个很好的问题！虽然 UUPS 逻辑合约确实增加了升级函数，但它仍然比透明代理更省 Gas。以下是详细的原因和解释：1. UUPS 的升级函数对 Gas 的影响在 UUPS 模式中，升级逻辑（如 upgradeTo）确实存在于逻辑合约中…
![【URP】Unity[纹理压缩]算法多平台对比](http://pic.xiahunao.cn/【URP】Unity[纹理压缩]算法多平台对比)
【URP】Unity[纹理压缩]算法多平台对比
纹理压缩技术发展节点 早期阶段 2000年代初 DXT/S3TC成为PC和主机平台主流，采用44像素块压缩，但移动端支持有限。 PVRTC（2008年）专为PowerVR GPU设计，要求纹理尺【从UnityURP开始探索游戏渲染】专栏-直达纹理…
AI元人文构想：三值纠缠模型
AI元人文构想：三值纠缠模型
作者：岐金兰
日期：2025年10月29日
引言：
观照个体欲望，尊重个体自感，于白箱化的价值博弈舞台，共同涌现集体客观——此三值纠缠模型，正是AI元人文构想跳动的心脏。
这精准道破，并庄…
EDK2环境搭建以及HelloWorld编译实现
本文简单介绍了Linux环境下搭建EDK2开发环境的关键步骤和命令。EDK2环境搭建以及HelloWorld编译实现
TianoCore的官方介绍
Welcome to TianoCore, the community supporting an open source implementation of the Uni…
谁生？谁死？从引用计数到可达性分析，洞悉GC的决策逻辑
谁生？谁死？从引用计数到可达性分析，洞悉GC的决策逻辑引用计数与可达性分析：谁死了，谁还活着？
垃圾回收，顾名思义，便是将已经分配出去的，但却不再使用的内存回收回来，以便能够再次分配。在Java虚拟机的语境下…
![P1561 [USACO12JAN] Mountain Climbing S](http://pic.xiahunao.cn/P1561 [USACO12JAN] Mountain Climbing S)
P1561 [USACO12JAN] Mountain Climbing S
Solution
简单看题容易得到一个错误的贪心：
\[ans=max\{\Sigma_{k=1}^n + down_{min}, \Sigma_{k=1}^n +up_{min}\}
\]然后你将可以把他 hack 掉，因为最初的方法认为第一个牛上山后，所有上下山是一起进行的，其实有…
六、阅读笔记六：保障软件可靠性的防线
《程序员修炼之道：从小工到专家》围绕软件测试与质量保障展开，系统阐述了如何通过科学的测试方法和质量管控策略，构建可靠的软件产品。在软件开发生命周期中，测试与质量保障是不可或缺的环节，它能够及时发现潜在问…
五、阅读笔记五 应对复杂系统的挑战
《程序员修炼之道：从小工到专家》聚焦于并发编程与系统性能优化，为应对复杂系统的技术挑战提供了全面的解决方案。随着软件系统的规模不断扩大，用户量持续增长，并发处理能力和系统性能成为衡量软件质量的重要指标。…
![P3988 [SHOI2013] 发牌](http://pic.xiahunao.cn/P3988 [SHOI2013] 发牌)
P3988 [SHOI2013] 发牌
Solution
容易发现，答案就是维护当前序列的第 k 大值，而且只有删除，这个时候就可以使用权值线段树来维护。这颗树的每一个叶子表示一张牌，然后线段树记录改节点为根的子树的节点个数，接着进行查询即可，代码见下…
文件夹显示绿色成功图标方法
链接：https://blog.csdn.net/jiminkoo/article/details/131840356本文来自博客园，作者：__username，转载请注明原文链接：https://www.cnblogs.com/code3/p/19172967
【RabbitMQ】与ASP.NET Core集成
本章目标掌握在ASP.NET Core中配置和依赖注入RabbitMQ服务。学习使用IHostedService/BackgroundService实现常驻消费者服务。实现基于RabbitMQ的请求-响应模式。构建完整的微服务间异步通信解决方案。学习配置管理和健…
IMO2025 Problem 1
考虑 \(n = 3\) 时的下三角，显然有三个容易构造的解，\(k = \{0, \, 1, \, 3\}\)，构造如下：那么 \(n > 3\) 呢？由于下三角的点数恰好为 \(1 + 2 + \cdots + n\) 个点，对于第一条直线，有且仅有 \(3\) 中方式覆…
Day6综合案例2-注册信息
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0">…