- 线性结构
- 线性表
- 顺序存储 —— 访问易,增删难
- 链式存储 —— 访问难、增删易
- 栈 —— 后进先出 和 队列 —— 先进先出
- 字符串 —— KMP 匹配算法
- 数组、矩阵和广义表
- 数组
- 树 —— 树根为第一层,最大层数为树高/深度
- 线索二叉树
- 哈夫曼编码
- 树和森林 —— 树的双亲表示和孩子表示
- 图
- 存储 —— 邻接矩阵、邻接表
- 遍历 —— DFS、BFS
- 最小生成树 —— Prim 算法和 Kruskal 算法
- 拓扑排序和关键路径
- 最短路径
- 单源点最短路径 —— Dijkstra 算法
- 每对顶点间的最短路径 —— Floyd 算法
- 查找
- 静态查找 —— 顺序查找、二分查找、分块查找
- 动态查找 —— 二叉排序树、平衡二叉树、B 树
- 哈希表
- 排序
线性结构
线性表的存储结构分为顺序存储和链式存储。
线性表
顺序存储 —— 访问易,增删难
以 L O C ( a 1 ) LOC(a_1) LOC(a1) 表示线性表中第一个元素的存储位置,在 顺序存储结构 中,第 i i i 个元素 a i a_i ai 的存储位置为
L O C ( a i ) = L O C ( a 1 ) + ( i − 1 ) × L LOC(a_i)=LOC(a_1)+(i-1) \times L LOC(ai)=LOC(a1)+(i−1)×L
其中, L L L 是表中每个数据元素所占空间的字节数。根据该计算关系,可随机存取表中的任一个元素。

线性表采用顺序存储结构的 优点是可以随机存取表中的元素,缺点是插入和删除操作需要移动元素。在插入前要移动元素以挪出空的存储单元,然后再插入元素;删除时同样需要移动元素,以填充被删除的元素空出来的存储单元。
在表长为 n n n 的线性表中插入新元素时,共有 n + 1 n+1 n+1 个插入位置,在位置 1 (元素所在位置)插入新元素,表中原有的 n n n 个元素都需要移动。
链式存储 —— 访问难、增删易
线性表的链式存储是用通过指针链接起来的结点来存储数据元素。数据域用于存储数据元素的值,指针域则存储当前元素的直接前驱或直接后继的位置信息,指针域中的信息称为指针(或链)。


在链式存储结构中,只需要 一个指针(称为头指针,如图3-2中的 head)指向第一个结点,就可以 顺序地访问到表中的任意一个元素。
在链式存储结构下进行 插入和删除,其实质都是 对相关指针的修改。

当线性表采用链表作为存储结构时,不能对数据元素进行随机访问,但是具有 插入和删除操作不需要移动元素 的优点。
栈 —— 后进先出 和 队列 —— 先进先出
字符串 —— KMP 匹配算法
主串为 abacbcabababbcbc,模式串为 abababb,且模式串的 next 函数值如下表所示,则 KMP 算法的匹配过程如图所示。其中,i 是主串字符的下标,j 是模式串字符的下标。

- 第一趟匹配从
S[0]与P[0]开始。由于S[0] = P[0]、S[1] = P[1]、S[2] = P[2],所以接下来比较S[3]与P[3],由于S[3]与P[3]不相等,所以第一趟结束。 - 要进行第二趟匹配,令
j = next[3](即j = 1)。第二趟从S[3]与P[1]开始比较,仍不相等,因此第二趟结束。 - 要进行第三趟匹配,所以令
j = next[1](即j = 0)。第三趟从S[3]与P[0]开始比较,由于S[3]与P[0]不相等,所以令j = next[0](即-1),此时满足条件j == -1,显然不能令S[3]与P[-1]进行比较,说明主串中从i=3开始的子串不可能与模式串相同,因此需要将i的值递增后再继续进行匹配过程,即令i++、j++。 - 下一趟从
S[4]与P[0]开始比较,继续匹配过程。直到某一趟匹配成功,或者由于在主串中找不到模式串而以失败结束。
数组、矩阵和广义表
数组与广义表可看作是线性表的推广,其特点是数据元素仍然是一个表。
数组

A A A 可看成一个行向量形式的线性表:

或列向量形式的线性表:

二维数组的存储结构可分为 以行为主序 和 以列为主序 的两种方法,

设每个数据元素占用 L L L 个单元, m m m、 n n n 为数组的行数和列数, L o c ( a 11 ) Loc(a_{11}) Loc(a11) 表示元素 a 11 a_{11} a11 的地址,那么以行为主序优先存储的地址计算公式为:
L o c ( a i j ) = L o c ( a 11 ) + ( ( i – 1 ) × n + ( j − 1 ) ) × L Loc(a_{ij}) = Loc(a_{11})+((i –1)\times n+(j−1)) \times L Loc(aij)=Loc(a11)+((i–1)×n+(j−1))×L
同理,以列为主序优先存储的地址计算公式为:
L o c ( a i j ) = L o c ( a 11 ) + ( ( j − 1 ) × m + ( i − 1 ) ) × L Loc(a_{ij}) = Loc(a_{11})+((j −1) \times m+(i -1))\times L Loc(aij)=Loc(a11)+((j−1)×m+(i−1))×L
推广至多维数组,在按下标顺序存储时,先排最右的下标,从右向左直到最左下标,而逆下标顺序则正好相反。
树 —— 树根为第一层,最大层数为树高/深度

- 结点的层次。根为第一层,根的孩子为第二层,依此类推,若某结点在第
i层,则其孩子结点在第i+1层。例如,图中,A 在第 1 层,B、C、D 在第 2 层,E、F 和 G 在第 3 层。 - 树的高度。一棵树的最大层数记为树的高度(或深度)。例如,图中所示树的高度为 3。



线索二叉树


哈夫曼编码
如果要设计长度不等的编码,必须满足下面的条件:任一字符的编码都不是另一个字符的编码的前缀,这种编码也称为前缀码。
设有字符集 {a,b,c,d,e} 及对应的权值集合 {0.30,0.25,0.15,0.22,0.08},按照构造最优二叉树的哈夫曼方法:先 按权值从低到高,先取字符 c 和所 e 对应的结点构造一棵二叉树(根结点的权值为 c 和 e 的权值之和),然后与 d 对应的结点分别作为左、右子树构造二叉树,之后选 a 和 b 所对应的结点作为左、右子树构造二叉树,最后得到的最优二叉树(哈夫曼树)如图所示。
其中,字符 a 的编码为 00,字符 b、c、d、e 的编码分别为 01、100、11、101。

译码时就从树根开始,若编码序列中当前编码为 0,则进入当前结点的左子树;为 1 则进入右子树,到达叶子时一个字符就翻译出来了,然后再从树根开始重复上述过程,直到编码序列结束。
例如,若编码序列 101110000100 对应的字符编码采用图所示的树进行构造,则可翻译出字符序列 edaac。
树和森林 —— 树的双亲表示和孩子表示


图
存储 —— 邻接矩阵、邻接表


遍历 —— DFS、BFS
最小生成树 —— Prim 算法和 Kruskal 算法
普里姆算法 构造最小生成树的过程是 以一个顶点集合 U = u 0 U={u_0} U=u0 作为初态,不断寻找与 U U U 中顶点相邻且代价最小的边的另一个顶点,扩充 U U U 集合直到 U = V U=V U=V 时为止。

克鲁斯卡尔求最小生成树的算法思想为:假设连通网 N = ( V , E ) N=(V,E) N=(V,E),令最小生成树的初始状态为只有 n n n 个顶点而无边的非连通图 T = ( V , { } ) T=(V,\{\}) T=(V,{}),图中每个顶点自成一个连通分量。在 E E E 中选择代价最小的边,若该边依附的顶点落在 T T T 中不同的连通分量上,则将此边加入到 T T T 中,否则舍去此边而选择下一条代价最小的边。依此类推,直到 T T T 中所有顶点都在同一连通分量上为止。

拓扑排序和关键路径

拓扑序列为 6,1,4,3,2,5。
最短路径
单源点最短路径 —— Dijkstra 算法

每对顶点间的最短路径 —— Floyd 算法
查找
静态查找 —— 顺序查找、二分查找、分块查找
动态查找 —— 二叉排序树、平衡二叉树、B 树
哈希表
排序
在排序过程中需要进行下列两种基本操作:比较两个关键字的大小;将记录从一个位置移动到另一个位置。前一种操作对大多数排序方法来说都是必要的,后一种操作可以通过改变记录的存储方式来避免。
各排序算法详见:十大排序算法
优学堂 算法
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 快速排序 | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( n 2 ) O(n^2) O(n2) | O ( l o g 2 n ) O(log_2\ n) O(log2 n) | 内部排序 | 不稳定 |
| 归并排序 | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( n ) O(n) O(n) | 外部排序 | 稳定 |
| 堆排序 | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( n l o g 2 n ) O(n\ log_2\ n) O(n log2 n) | O ( 1 ) O(1) O(1) | 内部排序 | 不稳定 |
| 希尔排序 | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 内部排序 | 不稳定 |
| 插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 内部排序 | 稳定 |
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 内部排序 | 稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 内部排序 | 不稳定 |
数组 基本有序 的情况下进行排序:
- 最适宜采用插入排序,时间复杂度为 O ( n ) O(n) O(n),空间复杂度为 O ( 1 ) O(1) O(1)。
- 对快速排序来说是 计算时间的最坏情况,时间复杂度为 O ( n 2 ) O(n^2) O(n2),空间复杂度为 O ( n ) O(n) O(n)。
- 快速排序在 “基本有序” 输入上退化到最坏情况的核心在于 枢轴(pivot)选择不当导致分区极度不平衡,使得递归树从理想的二叉树退化为一条链;
- 在简单实现中,若总是选择数组的第一个或最后一个元素作为枢轴,对于已经或几乎有序的数组,这些位置恰好是当前子数组的最小或最大值,导致 一次分区只剥离 1 个元素,剩余 n − 1 n-1 n−1 个元素集中在另一侧,完全失去 “分治” 优势。
在理想情况下,如果每次划分都恰好选择当前子数组的 真中位数 作为枢轴,那么快速排序就能保证 完全平衡 的递归分治:每次将规模为 n n n 的问题分解为两个规模为 n / 2 n/2 n/2 的子问题,再加上一次 O ( n ) O(n) O(n) 的划分工作。递归关系和时间复杂度:
T ( n ) = 2 T ( n 2 ) + O ( n ) ⟹ T ( n ) = O ( n log n ) . T(n) \;=\; 2\,T\bigl(\tfrac n2\bigr)\;+\;O(n) \quad\Longrightarrow\quad T(n)=O(n\log n). T(n)=2T(2n)+O(n)⟹T(n)=O(nlogn).
快速排序的空间复杂度:快速排序在变量(如基准值、索引和用于交换的临时变量)上使用恒定的额外空间 O ( 1 ) O(1) O(1),每次递归调用都会消耗栈空间,每层调用保存 O ( 1 ) O(1) O(1) 变量。
- 在平衡划分的情况下,递归深度为 O ( l o g n ) O(log\ n) O(log n),即 平均空间复杂度为 O ( l o g n ) O(log\ n) O(log n);
- 在不平衡划分的情况下,递归深度可以达到 n n n,即 最坏空间复杂度为 O ( n ) O(n) O(n)。
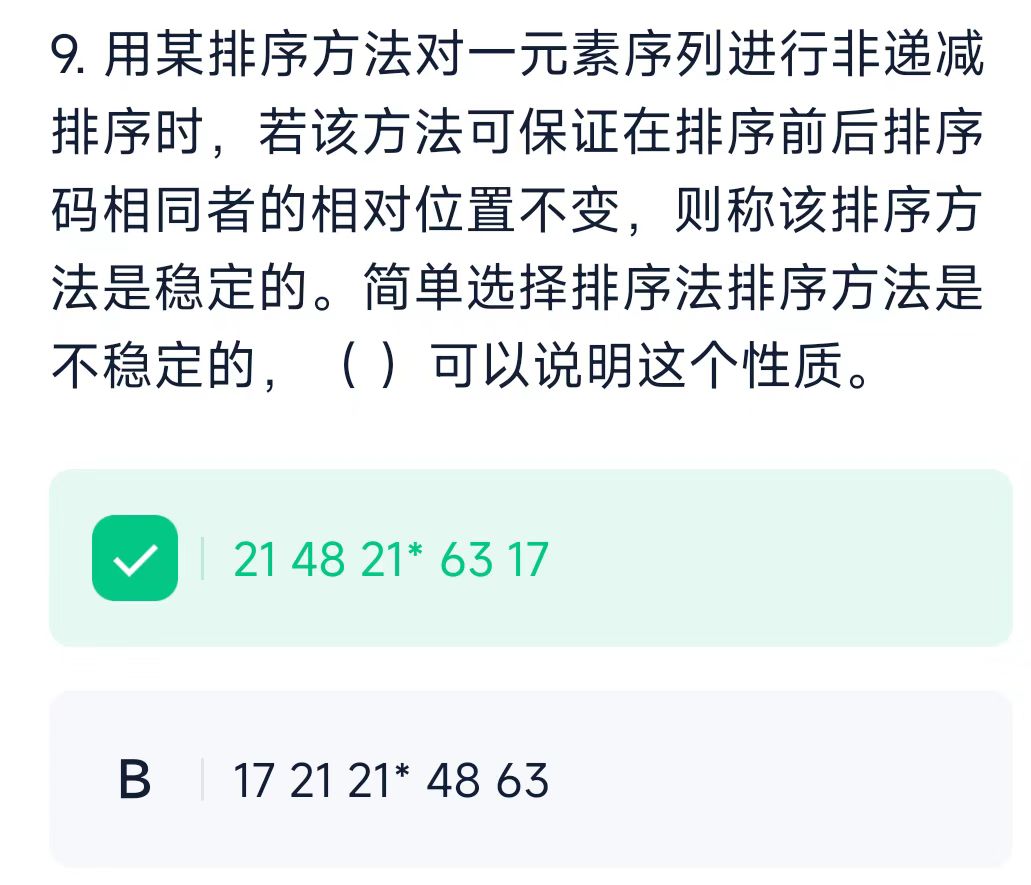
对 A 进行简单选择排序时,第一趟需交换 21 和 17,导致 21 与 21* 的相对位置发生变化。
- 该数组 基本有序,所以采用 直接插入 排序,需要进行的比较次数最少;
- 初始有序数组为 {1},后1与前1比较,不交换,
1, 1;2 与 1 比较,不交换,1, 1, 2;4 与 2 比较,不交换,1, 1, 2, 4;7 与 4 比较,不交换,1, 1, 2, 4, 7;5 与 7 比较,交换 5 和 7,继续往前比较,1, 1, 2, 4, 5, 7;5 与 4 比较,不交换,结束。- 注意最后的 5 不仅与 7 比较,还要与 4 比较。
- 对于 A, B 选项,以 A 为例, a 1 , a 2 . . . , a n a_1, a_2 ..., a_n a1,a2...,an 均比 b 1 b_1 b1 小,那么它们各自与 b 1 b_1 b1 比较一次即可,剩下有序数组 B 不需要比较直拼接到 a n a_n an 后即可。共需 n n n 次比较。
- 同理 D 选项的 b i / 2 + 1 b_{i/2+1} bi/2+1 到 b n b_n bn 都不需要比较直接拼接。
- 对于 C 选项, a 1 a_1 a1 和 b 1 b_1 b1 比较 a 1 a_1 a1 小,然后 a 2 a_2 a2 和 b 1 b_1 b1 比较 b 1 b_1 b1 小,继续 a 2 a_2 a2 和 b 2 b_2 b2 比较 a 2 a_2 a2 小,继续。。。
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 计数排序 | O ( n + k ) O(n + k) O(n+k) | O ( n + k ) O(n + k) O(n+k) | O ( n + k ) O(n + k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | 外部排序 | 稳定 |
| 桶排序 | O ( n + k ) O(n + k) O(n+k) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n + k ) O(n + k) O(n+k) | 外部排序 | 稳定 |
| 基数排序 | O ( n ∗ k ) O(n * k) O(n∗k) | O ( n ∗ k ) O(n * k) O(n∗k) | O ( n ∗ k ) O(n * k) O(n∗k) | O ( n + k ) O(n + k) O(n+k) | 外部排序 | 稳定 |
若一组 大规模 待排序记录的 关键字取值均在 0-9 之间,则适宜采用:计数 排序。



!!!)




 ✨ | Hidden Search Widget (交互式搜索框))








——QuickStart)



)