8.哈夫曼树

8.1 哈夫曼编码

哈夫曼编码（Huffman Coding），又称霍夫曼编码，是一种可变字长编码（VLC）方式

这种编码方法完全依据字符出现的概率来构造异字头的平均长度最短的码字， 因此有时也被称为最佳编码。

• 基本原理

  有5个字符a b c d e要发送

  a出现10次 b： 5 c： 3 d：20 f：1

  如果发送的要快 就要保证编码尽量短，这样就要求频率高的编码长度短，频率低的编码长度可以长一点。

• 基本步骤：

  • 计算字符频率：首先，统计每个字符在数据中出现的频率（次数）。

  • 构建哈夫曼树：根据字符的频率，使用自底向上的方法构建一棵哈夫曼树。在构建过程中，将 频率最低的两个节点合并为一个新的节点，其频率为两者之和，并将这两个字符分别作为新节 点的左右子节点。然后，将新节点加入到未处理的字符列表中，继续重复此过程，直到所有字 符都被合并到一个根节点下

    • 为什么选择最低的两个节点？

      • 因为频率最低路径也越长，编码长度也长

      • 通信原理里面可能少的比特数传输尽可能多的信息，以提高通信效率。将频率低的信号编码为较长的码字，可以使得频率高的信号占用较少的比特数，从而整体上减少传输的数据量

  • 生成编码：从根节点开始，为树中的每个字符生成一个唯一的编码

    对于每个非叶子节点，将 其左子节点的连接线标记为“0”，右子节点的连接线标记为“1”。字符的编码即为从根节点到该 字符叶子节点路径上的所有“0”和“1”的序列

特点：

• 高效性：由于字符编码的长度与其在数据中出现的频率成反比，因此高频字符使用较短的编

  码，而低频字符使用较长的编码，从而实现了数据的高效压缩。

• 唯一性：哈夫曼编码的码字是异前置码字，即任一码字不会是另一码字的前面部分（因为父节

  点是子节点的和），这使得各码字可以连在一起传送，中间不需另加隔离符号。

• 不唯一性：虽然哈夫曼树和编码的带权路径长度是唯一的，但哈夫曼树和编码本身并不唯一。

  在构建哈夫曼树时，如果两个字符的频率相等，它们可以以不同的顺序合并，从而导致不同的

  哈夫曼树和编码。

• 应用场景

• 文件和数据压缩：哈夫曼编码可用于文本、图像、音频等各种类型文件的压缩，通过减少文件

  大小来节省存储空间。

• 通信传输：在网络传输中，使用哈夫曼编码可以减小数据的大小，从而减少网络带宽的占用，

  加快数据传输速度。

• 无损压缩文件格式：GZIP、PKZIP、PNG和JPEG等文件格式都使用哈夫曼编码对文件中的数

  据进行压缩。

• 文本处理：在自然语言处理、文本挖掘等领域，哈夫曼编码可用于生成文本的索引、单词频率

  统计和特征向量表示等任务。

8.2 哈夫曼树

• 定义

哈夫曼树，也称为最优二叉树或最小带权路径长度树，是一种特殊的二叉树结构，其主要特点是带权路 径长度最短。

给定N个权值（频率/次数）作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，则 称这样的二叉树为最优二叉树，也称为哈夫曼树。

• 带权路径长度（WPL）

树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶 结点的层数）。计算公式为WPL = Σ(Wi * Li)，其中Wi表示叶子结点ki的权值，Li表示根结点到叶子结点 ki的路径长度

实际中权可能是金钱、时间成本等等

• 构造哈夫曼树

哈夫曼树的构造过程是自底向上的，步骤：

示例：已知字符集{ a, b, c, d, e, f }，若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 }

• 初始化：将给定的N个权值视为N棵只有根结点的二叉树（即叶子结点），这些二叉树构成初始森林。

  每个节点都当成一个树（树构成森林）

• 选择合并：在森林中选取两棵根结点的权值最小的树作为左右子树，构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。

  找两森林中两个权值最小的树，即b（3）和d（2）为左右子树，根节点的权值是二者之和

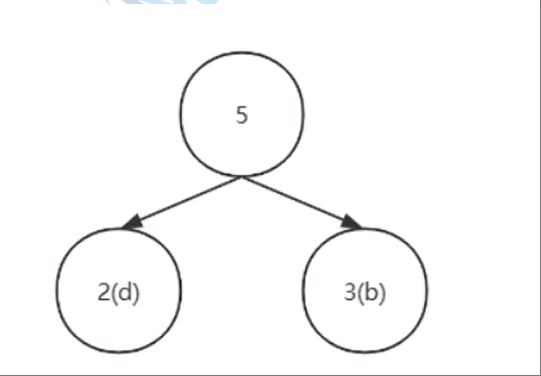
• 更新森林：在初始森林中删除这两棵树，同时将新得到的二叉树加入森林中**(左小右大**)。

• 重复操作：重复上述两个步骤，直到森林中只剩下一棵树为止。

再选出2个最小的数，选出了4（f）和5（上述步骤中组合后的父节点）

此时该森林中就有4棵树（a, c, e）以及上述图片中的树，权值分别为（6, 8, 10 ）

再选出2个最小的数，选出了6（a）和8（c）

此时该森林中就有3棵树（e）以及上述图片中两棵树的树，权值分别为（10 ） 再选出2个最小的数，选出了9和10（e）

此时该森林中就只有有上述图片中两棵树的树

将两棵树合并为一棵树

这棵树便是哈夫曼树。

• 哈夫曼编码

从根节点开始向下走往左为0，往右1。走到对应的字符的路径就是该字符的哈夫曼编码（左0右1）

最终的哈夫曼编码 左0 右1

高频字符使用较短的编码，而低频字符使用较长的编码

字符 权值 哈夫曼编码

a 6 00

b 3 1011

c 8 01

d 2 1010

e 10 11

f 4 100

#include <iostream>
#include <queue>
using namespace std;
// 哈夫曼树的节点（一个节点表示一棵树）
typedef struct  Node
{int weight; //权值struct  Node *left; //左孩子struct  Node *right;//右孩子
}TreeNode;// 哈夫曼树（(通过树表示森林)）
typedef struct  HumanTree
{// 树的根节点 通过这个根节点可以访问整棵树的所有节点Node *root;//下一个树，通过链表把树连起来变成森林struct HumanTree *nextTree;
}HumanTree;// 创建节点
Node *createNode(int weight)
{//分配内存Node *newNode = new Node{weight};// 初始化newNode->left =nullptr;newNode->right = nullptr;return newNode;
}// 创建哈夫曼树
HumanTree *createHumanTree(Node *root)
{// 变量名不能和类型名相同HumanTree *newTree = new HumanTree; // 初始化newTree->root = root;newTree->nextTree = nullptr;return newTree;
}//森林插入新树
void insertTree(HumanTree **tree, HumanTree *newtree)//第一个是森林 第二个是新树 因为森林会插入新树数量会修改，如果使用二级指针
{// 森林是空,森林就是新树if(!*tree){(*tree) = newtree;return;}// 中间节点指针 从第一颗树开始遍历HumanTree *current = (*tree);// 循环 使用current->nextTree和链表一样,如果是current到了null无法返回尾树了  while(current->nextTree){current = current->nextTree;}// 尾数处插入新树current->nextTree = newtree;}// 从森林中删除某棵树（并非真正删除，而是合并了）
void deleteTree(HumanTree **tree, HumanTree *deletetree)
{// 如果删除的是第一课树 头树if((*tree)->root->weight == deletetree->root->weight ){(*tree) =(*tree)->nextTree;delete deletetree;deletetree = nullptr;return;}// 不是第一颗树 遍历HumanTree *currentTree = (*tree);while(currentTree->nextTree){// 找到了要删除的树  currentTreeif(currentTree->nextTree->root->weight == deletetree->root->weight){// 更新森林currentTree->nextTree = currentTree->nextTree->nextTree;delete deletetree;deletetree = nullptr;return;}currentTree = currentTree->nextTree;}
}// 选择合并  在森林中选取两棵根结点的权值最小的树，构造一棵新的二叉树 会改变树的结构 用**
bool selectMerge(HumanTree **tree)
{// 空树或者只有一个节点if(!(*tree) || !(*tree)->nextTree){return false;}// 1. 找到权重最小的两棵树HumanTree *minTree1 = nullptr;//最小HumanTree  *minTree2 =nullptr;//第二小// 先从森林里找到前两棵来为最小的两棵树初始化if((*tree)->root->weight < (*tree)->nextTree->root->weight)//判断先两颗树谁打谁小{minTree1 = (*tree);minTree2 = (*tree)->nextTree;}else{minTree1 = (*tree)->nextTree;minTree2 = (*tree);}//   2.当前树（从第三棵树开始与前两棵书比较）   // 存储第三个节点HumanTree *current = (*tree)->nextTree->nextTree;// 比这个树都小while(current){// 比最小的小 之前最小的变成第二项，当前的变成最小if(current->root->weight < minTree1->root->weight){// 更新倒数第二小minTree2 = minTree1;// 更新最小minTree1 =  current;}// 比最二的小，最小的大 else if(current->root->weight < minTree2->root->weight && current->root->weight > minTree1->root->weight){// 更新倒数第二小minTree2 = current;}// 往后访问current = current->nextTree;}// 2. 合并这两棵树//  创建父节点 存储这两个节点(最小和第二小)TreeNode *newTreeNode =  createNode(minTree1->root->weight + minTree2->root->weight);//  创建新树 参数是新的父节点HumanTree *newTree = createHumanTree(newTreeNode);// 左小右大 将两棵树合并为一颗新树newTree->root->left = minTree1->root;newTree->root->right = minTree2->root;// 3. 将新树插入到森林insertTree(tree, newTree);//4. 删除原来的两棵树deleteTree(tree, minTree1);deleteTree(tree, minTree2);return true;
}// 打印哈夫曼编码
void printTree(TreeNode *p_code, string& code) // 传入节点   code是为其添加0 1
{// 空树if(!p_code){return;}//叶子节点，则打印字符和对应的编码if(p_code->left == nullptr && p_code->right == nullptr){cout << p_code->weight << ":"  << code << endl;}// 递归地遍历左右子树，并在当前编码的基础上添加'0'或'1'else{string leftNode = code + "0";string rightNode = code + "1";printTree( p_code->left, leftNode);printTree( p_code->right, rightNode);}
}// 清理函数(左右根)
void deintTree(TreeNode *node)
{if(!node ){return;}deintTree(node->left);deintTree(node->right);delete node;
}// 层次遍历（队列（一层一层遍历）
void levelPrint(HumanTree *p_tree)
{if(!p_tree){cout << "空树" << endl;return;}// 创建队列，存储树中每个节点 先进先出，符合层次遍历queue <TreeNode*>  q;// 先存储根节点q.push(p_tree->root);while(!q.empty()){// 保存根节点信息TreeNode *current = q.front();//一直保存根节点// 弹出根节点q.pop();// 访问当前节点cout.width(2);cout << current->weight << " ";// 如果左子节点存在，则加入队列if(current->left){q.push(current->left);}// 如果右子节点存在，则加入队列if(current->right){q.push(current->right);}}cout << endl;}// 主函数示例
int main()
{// 创建权值int weight[] = {6, 3, 8, 2, 10, 4};// 创建哈夫曼树HumanTree *newHumanTree  = nullptr;//  创建树节点for(int i = 0; i < sizeof(weight)/sizeof( weight[0]); i++){// 创建树并插入森林// insertTree插入树函数 newHumanTree取地址作为二级指针传入，是当前森林，createHumanTree是创建树// createHumanTree参数是节点createNode(weight[i])是创建节点后直接作为参数传入 createHumanTre中insertTree (&newHumanTree,createHumanTree(createNode(weight[i])));}// 选择合并while (selectMerge(&newHumanTree));//  // 层次遍历levelPrint(newHumanTree);// 打印哈夫曼编码string code = " ";printTree(newHumanTree->root, code);// 销毁树内节点deintTree(newHumanTree->root);// 销毁树delete newHumanTree;newHumanTree = nullptr;return 0;
}

根节点root是树的入口，通过它可以访问整棵树的所有其他节点*

找了一顿bug结果是 selectMerg if(!(*tree) || !(*tree)->nextTree)空树或者只有一个节点写错了写成 selectMerg if(!(*tree) || (*tree)->nextTree) 下次注意