40. 组合总和 II - 力扣（LeetCode）

class Solution {
private:vector<vector<int>>result;vector<int>path;void backtracking(vector<int>& candidates, int target,int sum,int startIndex,vector<bool>&used){if(sum==target){result.push_back(path);return;}for(int i=startIndex;i<candidates.size();i++){if(i>0&&candidates[i]==candidates[i-1]&&used[i-1]==false){continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); used[i] = false;sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool>used(candidates.size(),false);sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,0,used);return result;}
};

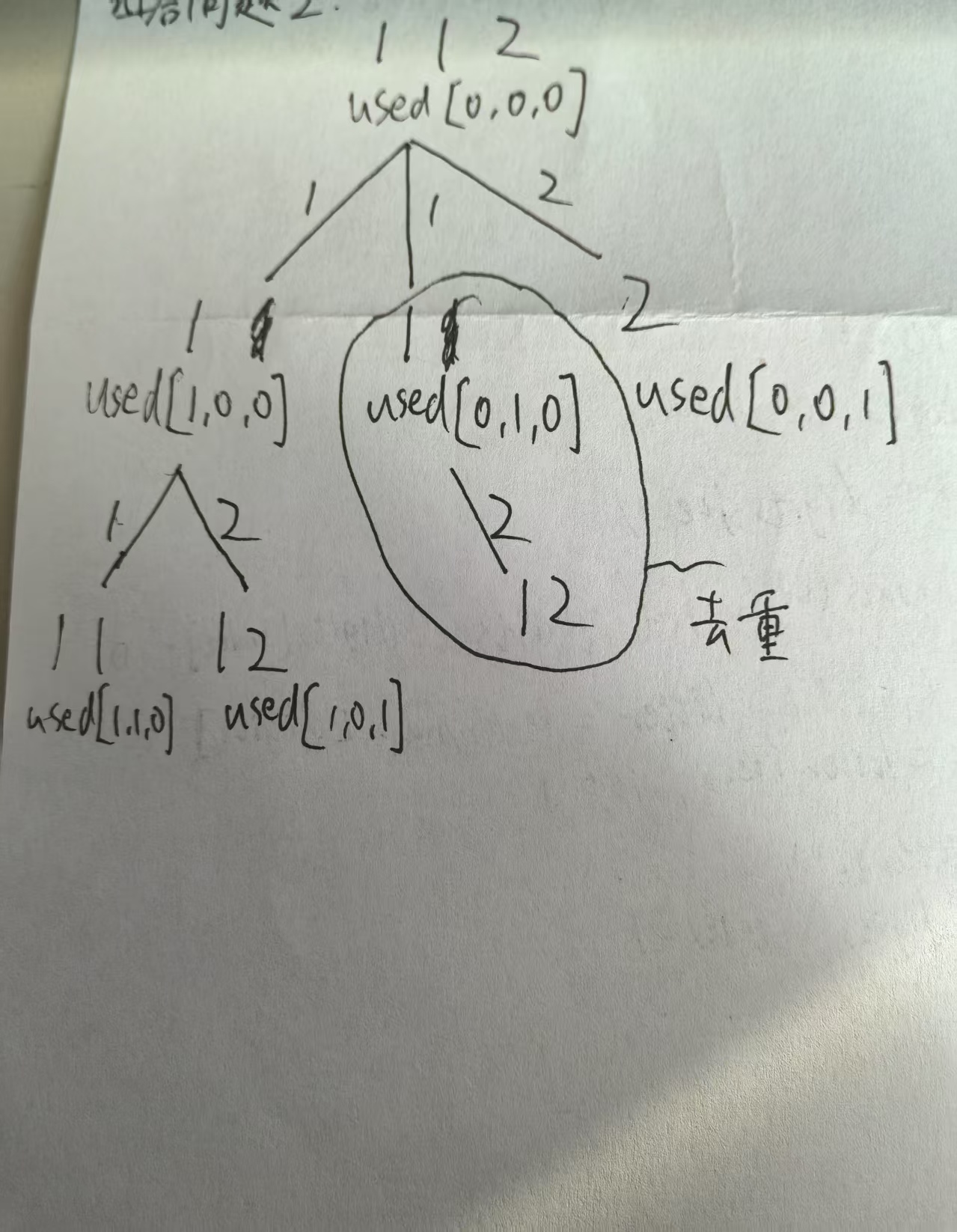
 元素的选取还是只取一次，构造树形结构，但不同的是要将初始数组排序，这样可以筛选出重复项，定义used数组，bool类型的，记录此元素是否被取过，如果两次取到元素相同，而且前一次取的used值为false则要进行去重。

 

组合问题（多条件）-CSDN博客 

其他逻辑与组合问题的逻辑一致，需要添加的是used数组的初始化，used的单层递归逻辑和回溯的逻辑。