万能欧几里得算法 笔记

\[\newcommand{\floor}[1]{\left\lfloor #1 \right\rfloor} \newcommand{\ceil}[1]{\left\lceil #1 \right\rceil} \renewcommand{\sf}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}} \renewcommand{\ss}[2]{\begin{Bmatrix} #1 \\ #2 \end{Bmatrix}} \renewcommand{\text}[1]{\operatorname{#1}} \newcommand{\lcm}[0]{\mathop{\text{lcm}}} \newcommand{\kmax}[0]{\mathop{\text{kthmax}}} \newcommand{\kmin}[0]{\mathop{\text{kthmin}}} \newcommand{\matrix}[1]{\begin{matrix}#1\end{matrix}} \newcommand{\bmatrix}[1]{\begin{bmatrix}#1\end{bmatrix}} \]

类欧几里得算法

类欧几里得算法常用于解决形如 \(\sum_i \floor{\frac{ai+b}c}\)（\(a, c > 0, b \ge 0\)）的问题。

代数推导，当 \(i\) 从 \(0\) 求和到 \(n\) 的答案为 \(f(n, a, b, c)\)：

• \(a>c \lor b > c\)，变为 \(f(n, a \bmod c, b \bmod c, c)\)。

• 考虑交换求和顺序，令 \(m=\floor{\frac{an+b}c}\)：

  \[\sum_{i=0}^n\floor{\frac{ai+b}c} = \sum_{j=0}^{m}\sum_{i=0} [j < \floor{\frac{ai+b}c}] \]

  对于 \(\floor{\frac{ai+b}c}\)，它等于 \(\ceil{\frac{ai+b+1}{c}} - 1\)。则有 \(j+1 < \ceil{\frac{ai+b+1}c}\)，变为 \(cj+c-b-1 < ai\)，可以得到 \(i > \floor{\frac{cj+c-b-1}{a}}\)。因此 \(f(n, a, b, c)\) 可以变为 \(f(m, c, c-b-1, a)\)。

\(n\) 这一维是单调减的，\(a\) 这一维每两步至少除以二，因此时间复杂度是 \(O(\log n)\) 的。

它的几何意义：

• 对第一步是把斜率大于等于 \(1\) 的都减去 \(\floor{k}\)。
• 对第二步则是把横纵坐标反转。

万能欧几里得算法

我们对类欧几里得算法进行了扩展，考虑一下它的几何意义。

考虑用折线来刻画一下这个求值。我们的直线每穿过一条横线的时候记为 \(U\)，穿过一条竖线记为 \(R\)。特别地，当它同时穿过横线和竖线的时候先 \(U\) 后 \(R\)。我们要求这个操作序列最后的位置为 \(R\)。

图例为 \(y=\frac{12.2x+2}{9}\)：

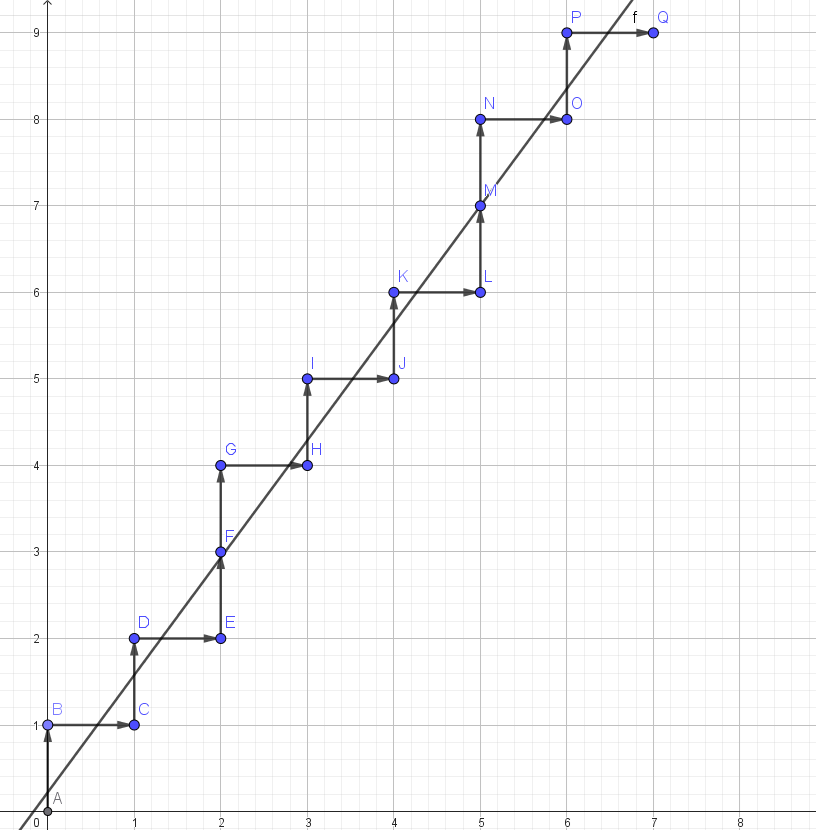
此时 \(x\) 轴为 \(i\)，我们维护 \(\floor{\frac{ai+b}{c}}\) 和 \(\sum\floor{\frac{ai+b}{c}}\) 的值。当 \(x \to x+1\) 时，\(\floor{\frac{ax+b}c}\) 会加 \(t\) 次（向上走 \(t\) 步），而 \(\sum\floor{\frac{ai+b}{c}}\) 会加上 \(\floor{\frac{ax+b}c}\)。我们使用矩阵维护（\(\bmatrix{\floor{\frac{ai+b}c} \\ \sum\floor{\frac{ai+b}c}}\)），则每次向上的时候让将其乘上 \(U\)，向右乘上 \(R\)。令 \(f(n, a, b, c, U, R)\) 为上述问题的答案（即有 \(n\) 个 \(R\)，第 \(i\) 个 \(R\) 前有 \(\floor{\frac{ai+b}c}\) 个 \(U\)，最后一个是 \(R\) 的答案），则：

• 当 \(b \ge c\) 的时候，答案为 \(U^{\floor{b/c}}f(n, a, b \bmod c, c, U, R)\)。

• 当 \(a \ge c\) 的时候，答案为 \(f(n, a \bmod c, b, c, U, U^{\floor{a/c}}R)\)。

  即我们变为

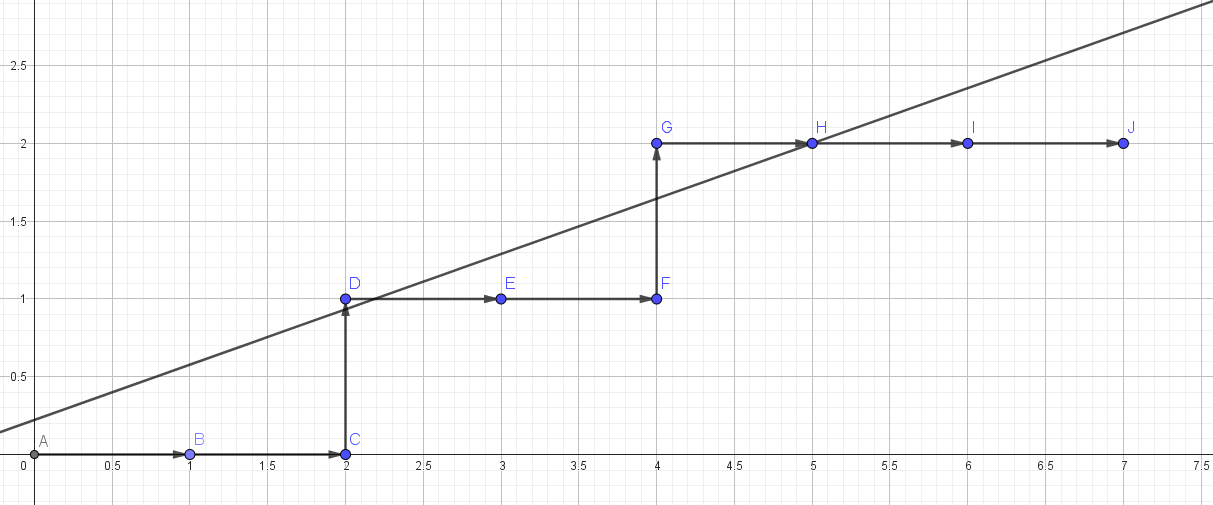
• 此时 \(a < c \land b < c\)，我们关于 \(y=x\) 对称，即我们对每个 \(U\) 统计其之前的 \(R\) 的个数（这样才能变为一个类似于欧几里得算法的形式）。（几何意义：对于整点的特殊情况，我们平移 \(\frac 1c\) 解决）

  

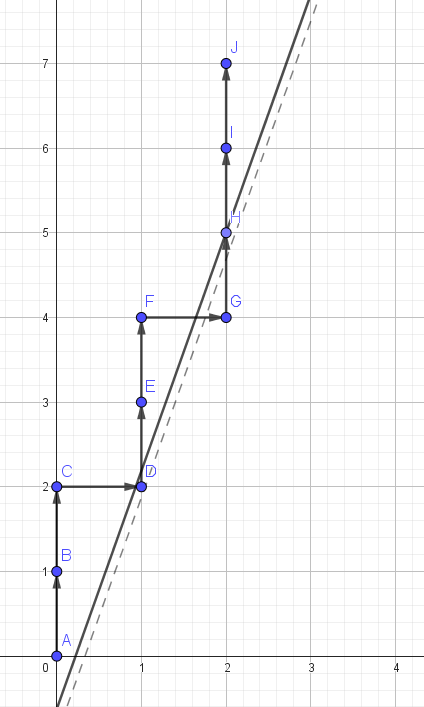
• 对于第 \(i\) 个 \(U\)，求 \(\sum_{j \ge 1} \left[\floor{\frac{aj+b}{c}} < i\right]\)。对 \(i > \floor{\frac{aj+b}c}\)，有之前的类似转化，变为：

  \[i > \frac{aj+b}c \]
  \[j < \frac{ci-b}a \]
  \[j < \ceil{\frac{ci-b}a} \]
  \[j \le \floor{\frac{ci-b-1}a} \]

  因此第 \(i\) 个 \(U\) 前会有 \(\floor{\frac{ci-b-1}a}\) 个 \(R\)，令 \(m = \floor{\frac{an+b}c}\)。我们可以把 \((n, a, b, c)\) 变为 \((m, c, -b-1, a)\)。但是 \(-b-1\) 是负数，我们初始要求 \(a, c \ge 0, b > 0\)。这一个可以直接把 \(i=1\) 的单独计算来解决。还有一个问题是我们要求最后一个是 \(R'\)（即 \(U\)），但是最后若干个变为了 \(U'\)（\(R\)）。因此我们也需要提出最后一个连续段。

  在提出 \(U^{\floor{\frac{c-b-1}{a}}}\) 后，第 \(x\) 个 \(R\) 前应有 \(\floor{\frac{cx+c-b-1}{a}} - \floor{\frac{c-b-1}{a}} = \floor{\frac {cx+(c-b-1)\bmod a}{a}}\)。最后应有 \(n-\floor{\frac{cm - b - 1}{a}}\) 个 \(R\)。

  即 \(f(n, a, b, c, U, R) = R^{\floor{(c-b-1)/a}}U\cdot f(m, c, (c-b-1)\bmod a, a, R, U) \cdot R^{n - \floor{\frac{cm-b-1}{a}}}\)。

  特别地，由于我们需要掐首去尾，我们特判 \(m=0\) 的情况，此时答案为 \(R^n\)。

练习1：P5170 【模板】类欧几里德算法

Problem

多组询问，每次给定 \(a, b, c, n\)。

求 \(\sum_{i\le n} \floor{\frac{ai+b}c}\)，\(\sum_{i\le n} i\floor{\frac{ai+b}c}\)，\(\sum_{i\le n} \floor{\frac{ai+b}c}^2\)。

Sol

令 \(y = \floor{\frac{ax+b}c}\)。需要维护 \(x, y, \sum x, \sum y, \sum y^2, \sum xy\) 的值。

遇到 \(U\) 时，\(y \gets y + 1\)。

遇到 \(R\) 时，\(x \gets x+1\)，\(sx \gets sx + x\)，\(sy \gets sy + y\)，\(sy2 \gets sy2 + y^2\)，\(sxy \gets sxy + xy\)。

考虑合并两个区间的信息。则有 \(x = x_l + x_r\)，\(y = y_l + y_r\)，\(sx = sx_l + sx_r + x_l\cdot x_r\)，\(sy = sy_l + sy_r + y_l \cdot x_r\)，\(sy2 = sy2_l + sy2_r + x_ry_l^2 + 2y_l\cdot sy_r\)，\(sxy = sxy_l + sxy_r + x_rx_ly_l + x_lsy_r + y_lsx_r\)。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int P = 998244353;
struct Node {ll x, y, sx, sy, sy2, sxy;Node() : x(0), y(0), sx(0), sy(0), sy2(0), sxy(0) {}Node(ll _x, ll _y, ll _sx, ll _sy, ll _sy2, ll _sxy) : x(_x), y(_y), sx(_sx), sy(_sy), sy2(_sy2), sxy(_sxy) {}friend Node operator*(const Node &l, const Node &r) {Node res;res.x = (l.x + r.x) % P;res.y = (l.y + r.y) % P;res.sx = (l.sx + r.sx + l.x * r.x) % P;res.sy = (l.sy + r.sy + l.y * r.x) % P;res.sy2 = (l.sy2 + r.sy2 + r.x * l.y % P * l.y + 2 * l.y * r.sy) % P;res.sxy = (l.sxy + r.sxy + r.x * l.x % P * l.y % P + l.x * r.sy + l.y * r.sx) % P;return res;}
};
Node QPow(Node a, ll b) {Node res;for (; b; b >>= 1, a = a * a)if (b & 1)res = res * a;return res;
}
Node F(ll n, ll a, ll b, ll c, Node U, Node R) {if (!n) return Node();if (b >= c) return QPow(U, b / c) * F(n, a, b % c, c, U, R);if (a >= c) return F(n, a % c, b, c, U, QPow(U, a / c) * R);ll m = (a * n + b) / c;if (!m) return QPow(R, n);return QPow(R, (c - b - 1) / a) * U * F(m - 1, c, (c - b - 1) % a, a, R, U) * QPow(R, n - (c * m - b - 1) / a);
}
int main() {Node U, R;U.y = 1;R.x = 1, R.sx = 1;int T;scanf("%d", &T);while (T--) {ll n, a, b, c;scanf("%lld%lld%lld%lld", &n, &a, &b, &c);Node ret = F(n, a, b, c, U, R);ret.sy += b / c;ret.sy2 += (b / c) * (b / c);printf("%lld %lld %lld\n", ret.sy % P, ret.sy2 % P, ret.sxy);}return 0;
}

练习2：

Problem

求：

\[C=\sum\limits_{x=1}^LA^xB^{\left\lfloor\frac{Px+R}{Q}\right\rfloor} \]

其中 \(A,B\) 是 \(N\) 行 \(N\) 列的矩阵。\(N \le 20, L,\floor{\frac{PL}{Q}} \le 10^{18}\)。

我们维护 \(\prod A, \prod B,\sum A^iB^j\)。

遇到 \(U\) 时：\(pb \gets pb \cdot B\)。

遇到 \(R\) 时：\(pa \gets pa \cdot A\)，\(sab \gets sab + pa\cdot pb\)。

考虑合并左右区间的信息。有 \(pa = pa_l \cdot pa_r\)，\(pb = pb_l\cdot pb_r\)，\(sab = sab_l + pa_l\cdot sab_r\cdot b_l\)，这个是因为 \(pb_l, B^k\) 都是 \(B\) 的次幂，所以能交换。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef __int128_t i128;
const int P = 998244353;
struct Matrix {int n, m;ll a[25][25];Matrix() : n(0), m(0) { memset(a, 0, sizeof (a)); }Matrix(int _n) : n(_n), m(_n) {memset(a, 0, sizeof (a));for (int i = 1; i <= n; i++) a[i][i] = 1;}Matrix(int _n, int _m) : n(_n), m(_m) { memset(a, 0, sizeof (a)); }ll *operator[](int x) { return a[x]; }const ll *operator[](int x) const { return a[x]; }friend Matrix operator+(const Matrix &a, const Matrix &b) {Matrix c(a.n, a.m);for (int i = 1; i <= a.n; i++)for (int j = 1; j <= a.m; j++)c[i][j] = (a[i][j] + b[i][j]) % P;return c;}friend Matrix operator*(const Matrix &a, const Matrix &b) {Matrix c(a.n, b.m);for (int i = 1; i <= a.n; i++)for (int k = 1; k <= a.m; k++)for (int j = 1; j <= b.m; j++)(c[i][j] += a[i][k] * b[k][j]) %= P;return c;}
};
int m;
struct Node {Matrix x, y, s;Node() : x(m), y(m), s(m, m) {}friend Node operator*(const Node &l, const Node &r) {Node res;res.x = l.x * r.x;res.y = l.y * r.y;res.s = l.s + l.x * r.s * l.y;return res;}
};
Node QPow(Node a, ll b) {Node res;for (; b; b >>= 1, a = a * a)if (b & 1)res = res * a;return res;
}
Node F(ll n, ll a, ll b, ll c, Node U, Node R) {if (!n) return Node();if (b >= c) return QPow(U, b / c) * F(n, a, b % c, c, U, R);if (a >= c) return F(n, a % c, b, c, U, QPow(U, a / c) * R);ll m = ((i128) a * n + b) / c;if (!m) return QPow(R, n);return QPow(R, (c - b - 1) / a) * U * F(m - 1, c, (c - b - 1) % a, a, R, U) * QPow(R, n - ((i128) c * m - b - 1) / a);
}
ll a, b, c, n;
int main() {scanf("%lld%lld%lld%lld%d", &a, &c, &b, &n, &m);Node U, R;for (int i = 1; i <= m; i++)for (int j = 1; j <= m; j++)scanf("%lld", &R.x[i][j]), R.s[i][j] = R.x[i][j];for (int i = 1; i <= m; i++)for (int j = 1; j <= m; j++)scanf("%lld", &U.y[i][j]);Node ans = F(n, a, b, c, U, R);for (int i = 1; i <= m; i++)for (int j = 1; j <= m; j++)printf("%lld%c", ans.s[i][j], " \n"[j == m]);return 0;
}