刘二大人PyTorch深度学习实践第二讲笔记

碎碎念：
开个新坑，系统学一遍深度学习好做毕设，能到河工大挺激动的，赶紧给刘二大人投自荐简历，但是已读不回，还是自己太菜了........不过已经到河工大了挺好的，梦校

第二讲

线性模型

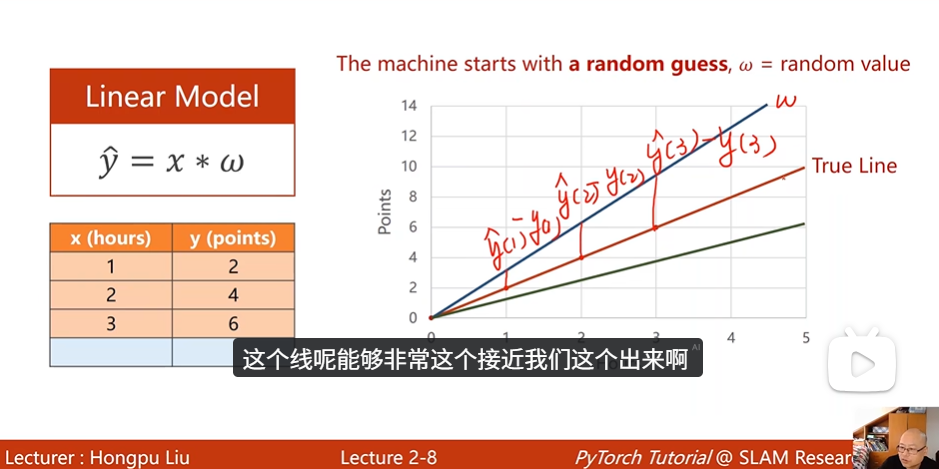
可能x（输入）到y（答案）是一个线性模型，但是w或者其他的权重值不确定，所以机器随机选取权重数值，看看哪个公式得到的预期答案和真实答案偏差较小，就是训练的最优模型

评价方法MSE:（假设x到y的映射就是简单的y=x*w）

（模型预期值-真实值）的平方再平均，就是MSE（均方误差）

还是假设y=w*x，找出最佳权重：

import numpy as np
import matplotlib.pyplot as pltx_data=[1.0,2.0,3.0]
y_data=[3.0,6.0,9.0]def forward(x):return x*wdef loss(x,y):y_pred=forward(x)return (y_pred-y)*(y_pred-y)w_list=[]
mse_list=[]for w in np.arange(0.0,4.1,0.1):print("w=",w)l_sum=0for x_val,y_val in zip(x_data,y_data):y_pred_val=forward(x_val)loss_val=loss(x_val,y_val)l_sum+=loss_valprint('\t',x_val,y_val,y_pred_val,loss_val)print('MSE = ',l_sum/3)w_list.append(w)mse_list.append(l_sum/3)
plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

结果：

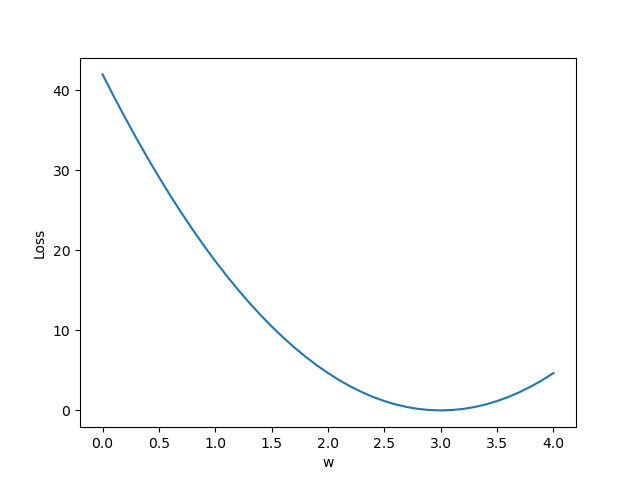
再试一个y=w*x+b的

# import numpy as np
# import matplotlib.pyplot as plt
#
# x_data=[1.0,2.0,3.0]
# y_data=[3.0,6.0,9.0]
#
#
# def forward(x):
#     return x*w
#
# def loss(x,y):
#     y_pred=forward(x)
#     return (y_pred-y)*(y_pred-y)
#
# w_list=[]
# mse_list=[]
#
# for w in np.arange(0.0,4.1,0.1):
#     print("w=",w)
#     l_sum=0
#     for x_val,y_val in zip(x_data,y_data):
#         y_pred_val=forward(x_val)
#         loss_val=loss(x_val,y_val)
#         l_sum+=loss_val
#         print('\t',x_val,y_val,y_pred_val,loss_val)
#     print('MSE = ',l_sum/3)
#     w_list.append(w)
#     mse_list.append(l_sum/3)
# plt.plot(w_list,mse_list)
# plt.ylabel('Loss')
# plt.xlabel('w')
# plt.show()import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Dx_data=[1.0,2.0,3.0]
y_data=[4.0,7.0,10.0]
def forward(x):return x*w+b
def loss(x,y):y_pred=forward(x)return (y_pred-y)*(y_pred-y)
w_list=[]
b_list=[]
mse_list=[]for w in np.arange(0.0,4.1,0.1):for b in np.arange(0.0,4.1,0.1):l_sum=0for x_val,y_val in zip(x_data,y_data):y_pred_val=forward(x_val)loss_val=loss(x_val,y_val)l_sum+=loss_val#     print('\t',x_val,y_val,y_pred_val,loss_val)# print('MSE = ',l_sum/3)w_list.append(w)b_list.append(b)mse_list.append(l_sum/3)# 转换为numpy数组并重塑为网格格式
w_array = np.array(w_list)
b_array = np.array(b_list)
mse_array = np.array(mse_list)# 创建网格数据
w_unique = np.unique(w_array)
b_unique = np.unique(b_array)
W, B = np.meshgrid(w_unique, b_unique)
MSE = mse_array.reshape(len(b_unique), len(w_unique))# 绘图
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')# 使用plot_surface绘制曲面
surf = ax.plot_surface(W, B, MSE, cmap='viridis', alpha=0.8)ax.set_xlabel('权重 w')
ax.set_ylabel('偏置 b')
ax.set_zlabel('MSE 损失')
ax.set_title('损失函数曲面: y = w*x + b')# 添加颜色条
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)# 找到最小MSE的点
min_idx = np.argmin(mse_array)
best_w = w_array[min_idx]
best_b = b_array[min_idx]
best_mse = mse_array[min_idx]# 标记最优点
ax.scatter([best_w], [best_b], [best_mse], color='red', s=100, label=f'最优: w={best_w:.1f}, b={best_b:.1f}')
ax.legend()plt.show()print(f"最优参数: w = {best_w:.1f}, b = {best_b:.1f}")
print(f"最小MSE: {best_mse:.4f}")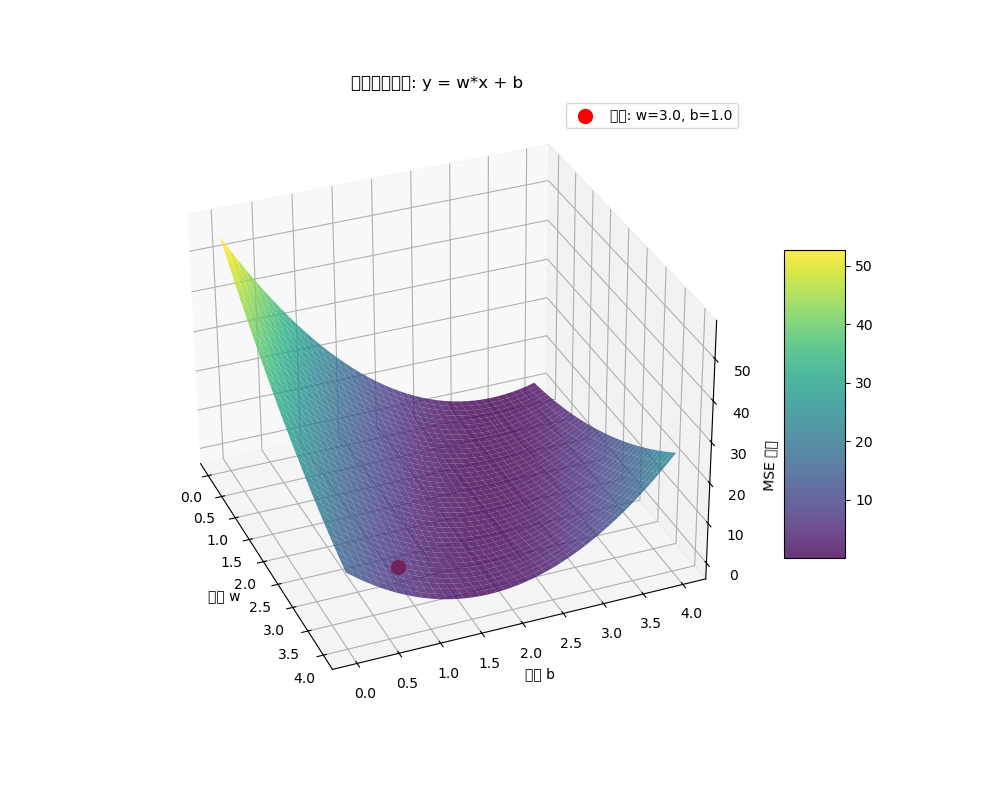

• 坐标网格: W 和 B
• 值网格: MSE

最后的坐标网络,W和B也各自是二维数组，这样才能和MSE组成一个3维图

这段有点难理解，ai写了下

# 转换为numpy数组并重塑为网格格式
w_array = np.array(w_list)
b_array = np.array(b_list)
mse_array = np.array(mse_list)# 创建网格数据
w_unique = np.unique(w_array)
b_unique = np.unique(b_array)
W, B = np.meshgrid(w_unique, b_unique)
MSE = mse_array.reshape(len(b_unique), len(w_unique))

最后几段分步详解

我们来一步步拆解每一行代码：

1. w_unique = np.unique(w_array)

• w_array

  这是一个一维的 NumPy 数组，里面存储了一系列的权重（weight）值。这些值可能有重复。

  • 例如：w_array = [1, 2, 2, 3, 3, 3]

• np.unique(): 这是 NumPy 的一个函数，它会返回输入数组中排序后的唯一值（即去重后的值）。

• 结果 w_unique

  它将是

  w_array
  

  中所有不重复的权重值，并按从小到大排列。

  • 例如：w_unique = [1, 2, 3]

这一步的目的是：找出所有不同的权重值，作为我们后续网格的 X 轴坐标。

2. b_unique = np.unique(b_array)

• b_array

  这是一个一维的 NumPy 数组，里面存储了一系列的偏置（bias）值。这些值也可能有重复。

  • 例如：b_array = [4, 4, 5, 5, 6]

• 结果 b_unique

  它将是

  b_array
  

  中所有不重复的偏置值，并按从小到大排列。

  • 例如：b_unique = [4, 5, 6]

这一步的目的是：找出所有不同的偏置值，作为我们后续网格的 Y 轴坐标。

3. W, B = np.meshgrid(w_unique, b_unique)

• np.meshgrid(): 这是最关键的一步。它接收两个一维数组，并返回两个二维数组。这两个二维数组共同构成了一个网格的坐标。

  • 它会以第一个输入数组（w_unique）为列，以第二个输入数组（b_unique）为行，创建一个二维坐标网格。

• 结果 W 和 B:

  • W 是一个二维数组，它的每一行都是 w_unique。
  • B 是一个二维数组，它的每一列都是 b_unique。

• 举例说明：

  • 输入: w_unique = [1, 2, 3], b_unique = [4, 5, 6]

  • 输出:

    W = [[1 2 3][1 2 3][1 2 3]]B = [[4 4 4][5 5 5][6 6 6]]
    

  • 这样，W 和 B 就共同定义了一个 3x3 的网格，每个网格点的坐标 (W[i][j], B[i][j]) 都对应一个 (权重, 偏置) 的组合。

这一步的目的是：创建一个完整的二维坐标网格，覆盖所有可能的(权重, 偏置)组合。

4. MSE = mse_array.reshape(len(b_unique), len(w_unique))

• mse_array: 这是一个一维的 NumPy 数组，里面存储了与w_array和b_array中每一组(w, b)相对应的均方误差（Mean Squared Error）值。
  • 它的长度必须与w_array和b_array相同。
  • 例如，如果 w_array 和 b_array 都有 6 个元素，mse_array 也必须有 6 个元素。
• len(b_unique) 和 len(w_unique): 它们分别是网格的行数和列数。在我们的例子中，行数是 3，列数是 3。
• reshape(...): 这个函数将一维的mse_array转换成一个二维数组。
  • 非常重要：reshape 函数默认是 ** 按行优先（C-style）** 的顺序重新排列元素的。这意味着，mse_array 中的元素必须是按照与 np.meshgrid 生成网格时相同的顺序排列的。
  • 也就是说，mse_array 的元素顺序应该是先固定b，再遍历w。例如：[mse(w=1,b=4), mse(w=2,b=4), mse(w=3,b=4), mse(w=1,b=5), ...]
• 结果 MSE: 一个二维的 MSE 数组，它的形状是 (网格行数, 网格列数)，也就是 (len(b_unique), len(w_unique))。
  • 这个二维数组MSE中的每一个元素MSE[i][j]，都对应于网格坐标(W[i][j], B[i][j])处的均方误差值。

这一步的目的是：将一维的 MSE 值数组，按照我们创建的网格形状，重新组织成一个二维的 MSE 矩阵。

---

总结：为什么要这么做？

假设你有一批数据点 (w, b, mse)，它们可能是这样散落的：

• (1, 4, 0.1)
• (2, 4, 0.2)
• (3, 4, 0.15)
• (1, 5, 0.3)
• ...

通过上述四行代码，你将这些散落的数据点，整理成了一个结构化的、可以直接用于绘图的二维数据结构：

• 坐标网格: W 和 B
• 值网格: MSE

这样，你就可以使用像 matplotlib 这样的库，轻松地绘制出一张关于 w 和 b 的 MSE 热力图（imshow(MSE)），或者一个 3D 曲面图（plot_surface(W, B, MSE)），从而直观地看到在不同的权重和偏置组合下，模型的误差是如何变化的。这对于寻找最优的模型参数非常有帮助。