第二讲类神经网络训练不起来
一.优化失败的原因
![image]()
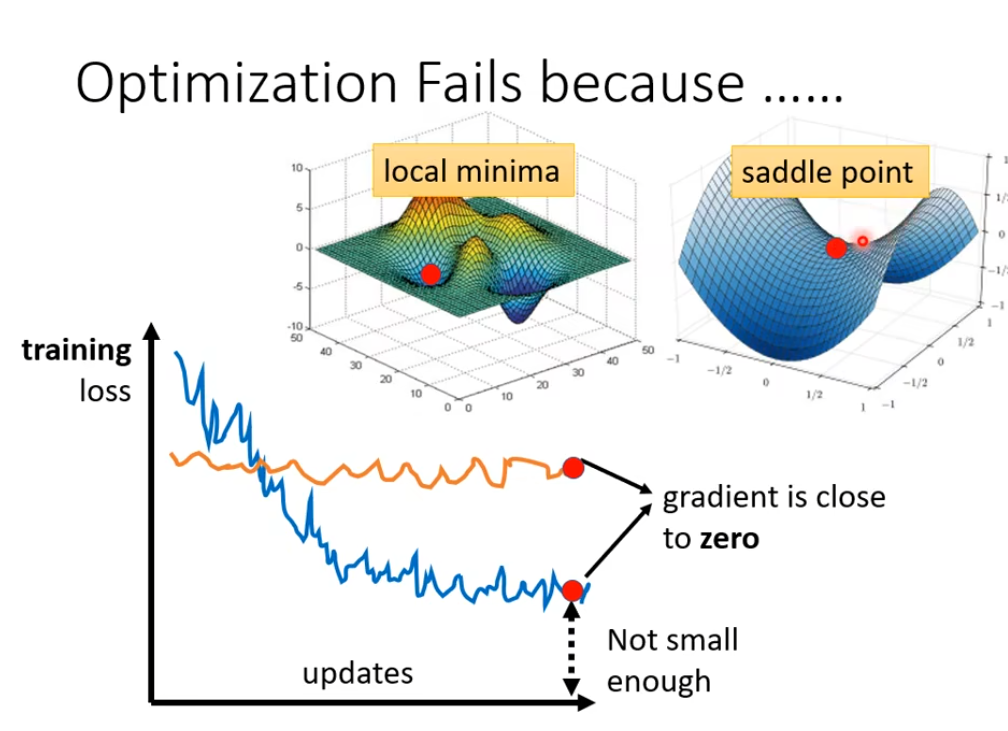
梯度为0有可能是local minima 和saddle point
因为计算优化的终止条件是梯度为0,但有可能梯度为0仅是局部最小值local minima或鞍点saddle point(多维,在某些维度是最小值,某些维度是最大值。)
![image]()
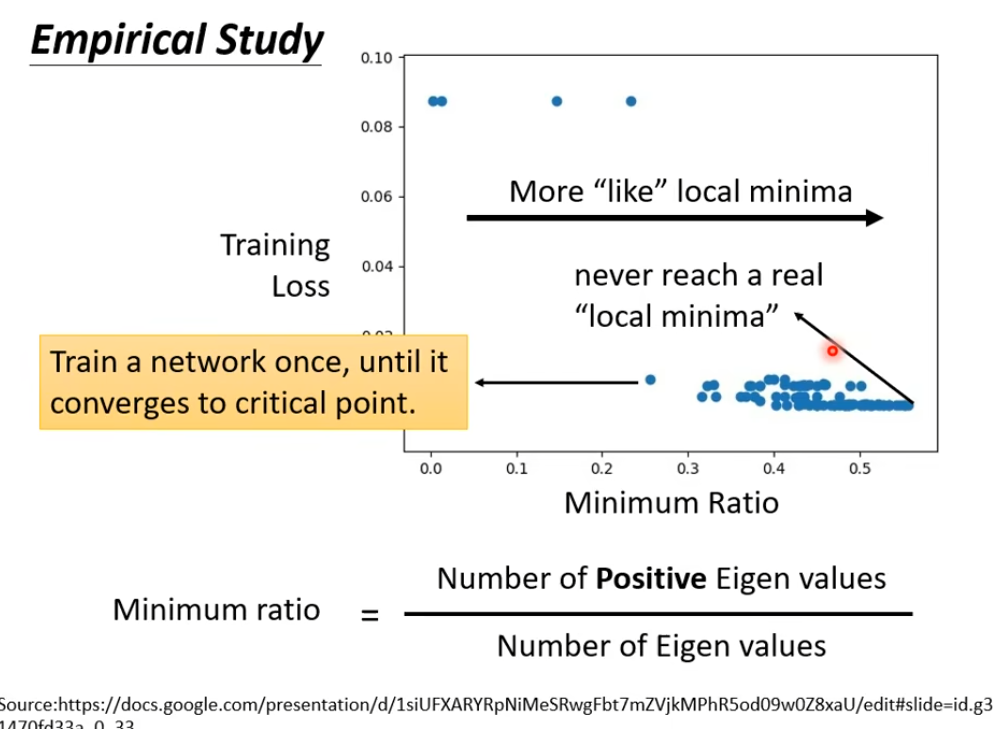
eigen特征值
如果minimum ratio越偏向1则为local minima
因为有正有负样本的情况是saddle point
二.Batch
![image]()
![image]()
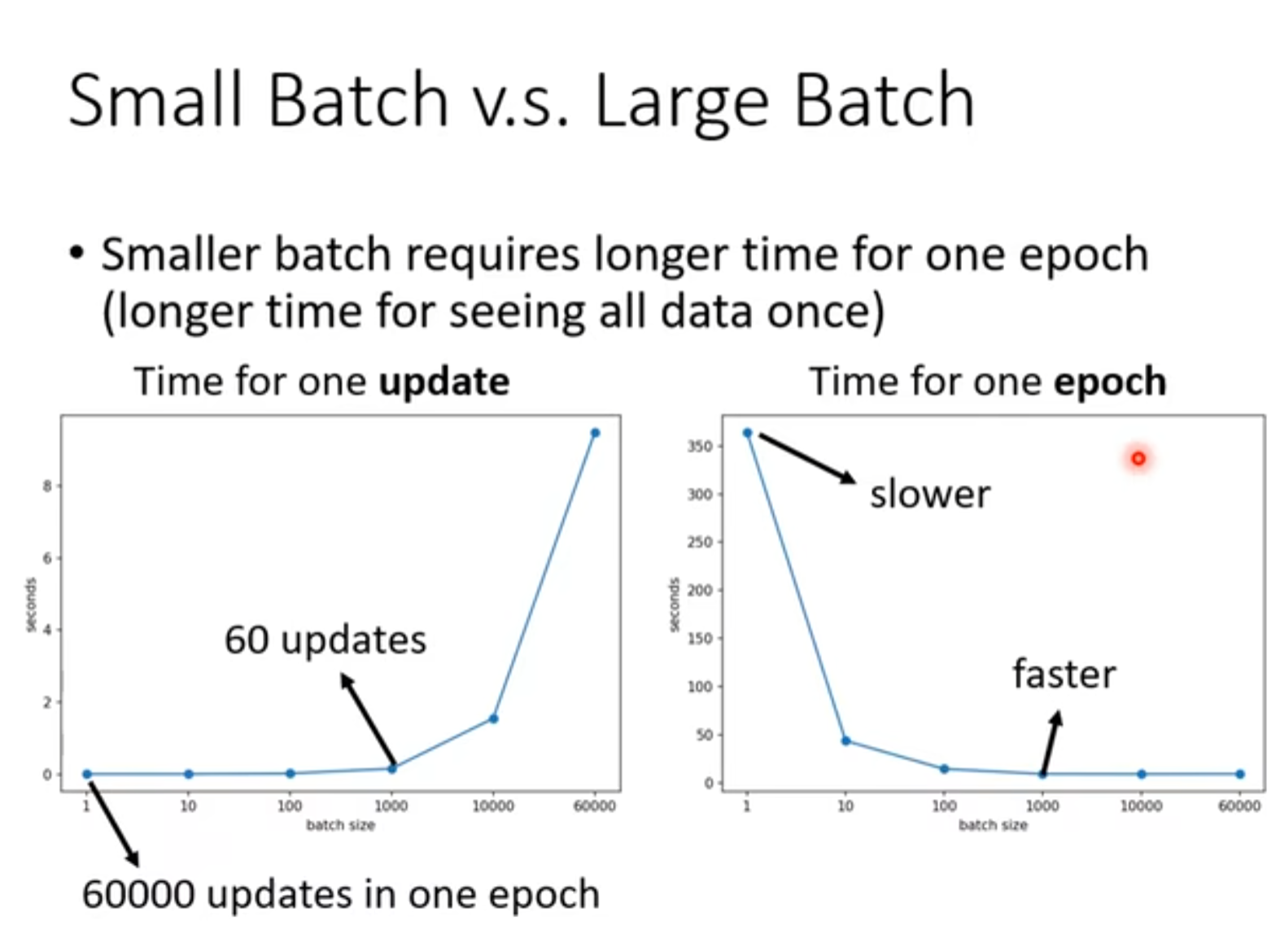
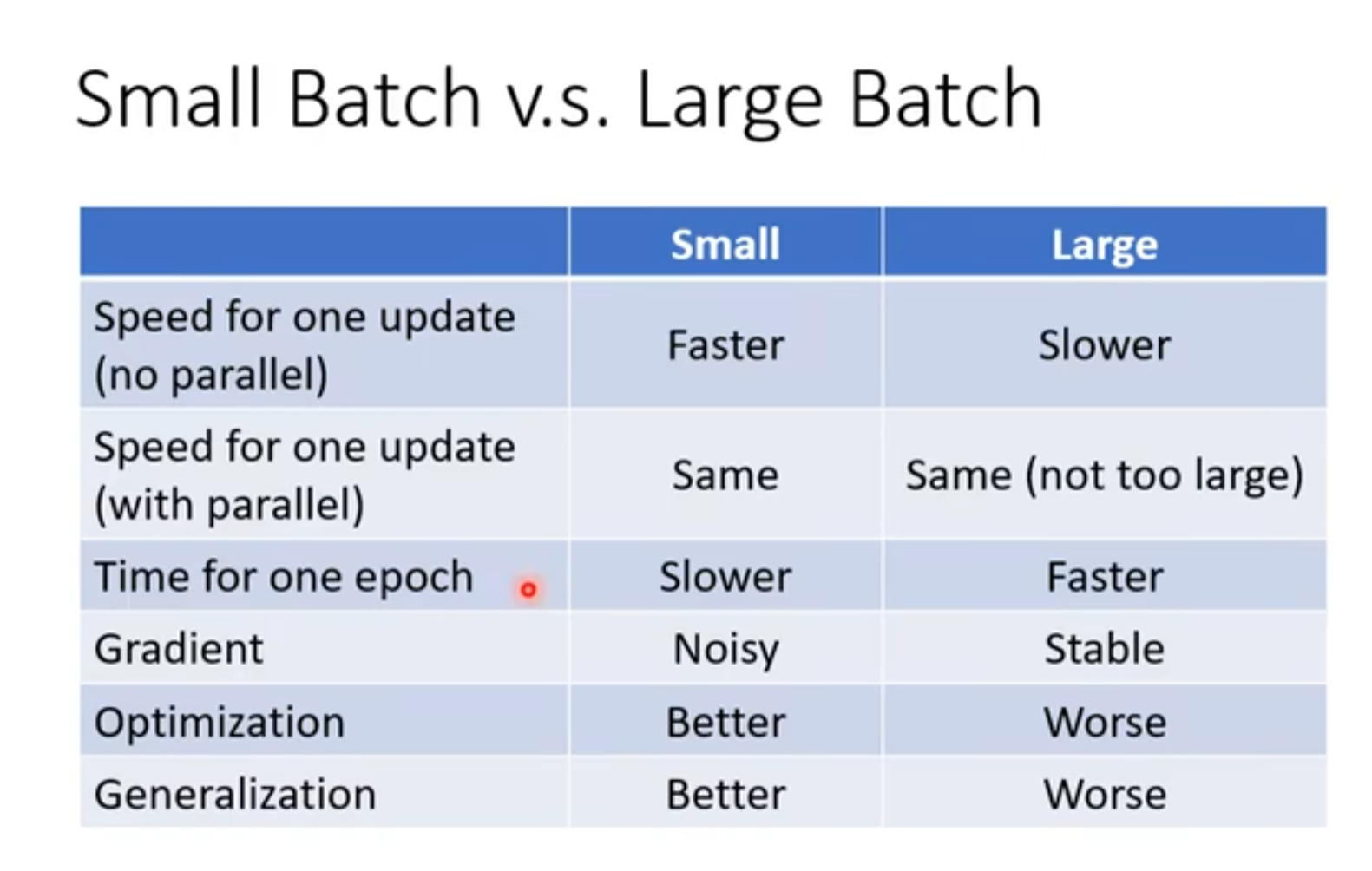
batch大的更新一次慢更新一整个epoch整个样本会更快
![image]()
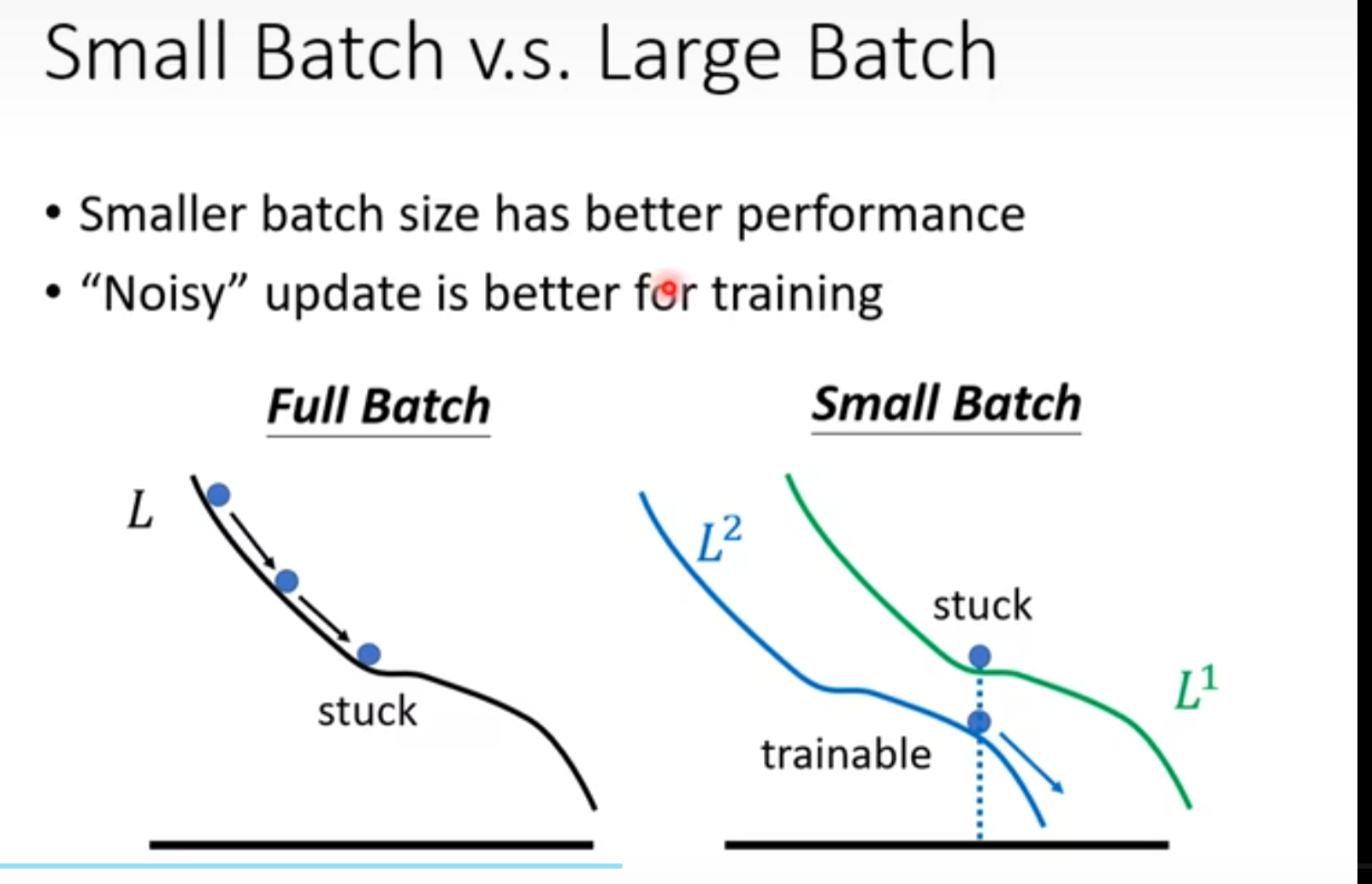
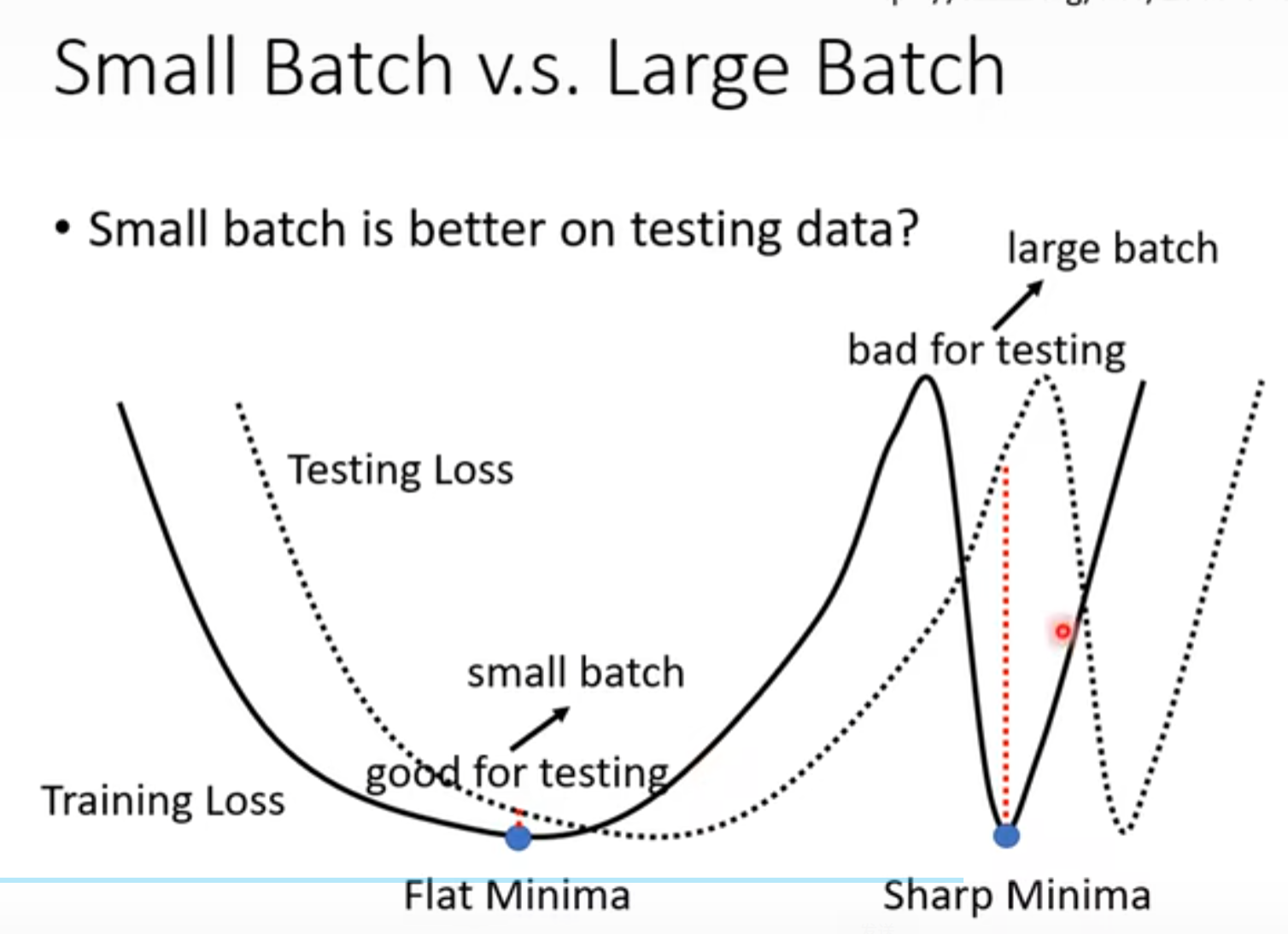
batch小的有益于training!
![image]()
batch小的偏向于flat minima
batch大的偏向于sharp minima
当曲线偏移时,flat minima峡谷影响较小,sharp minima影响大
![image]()
batch size 超参数
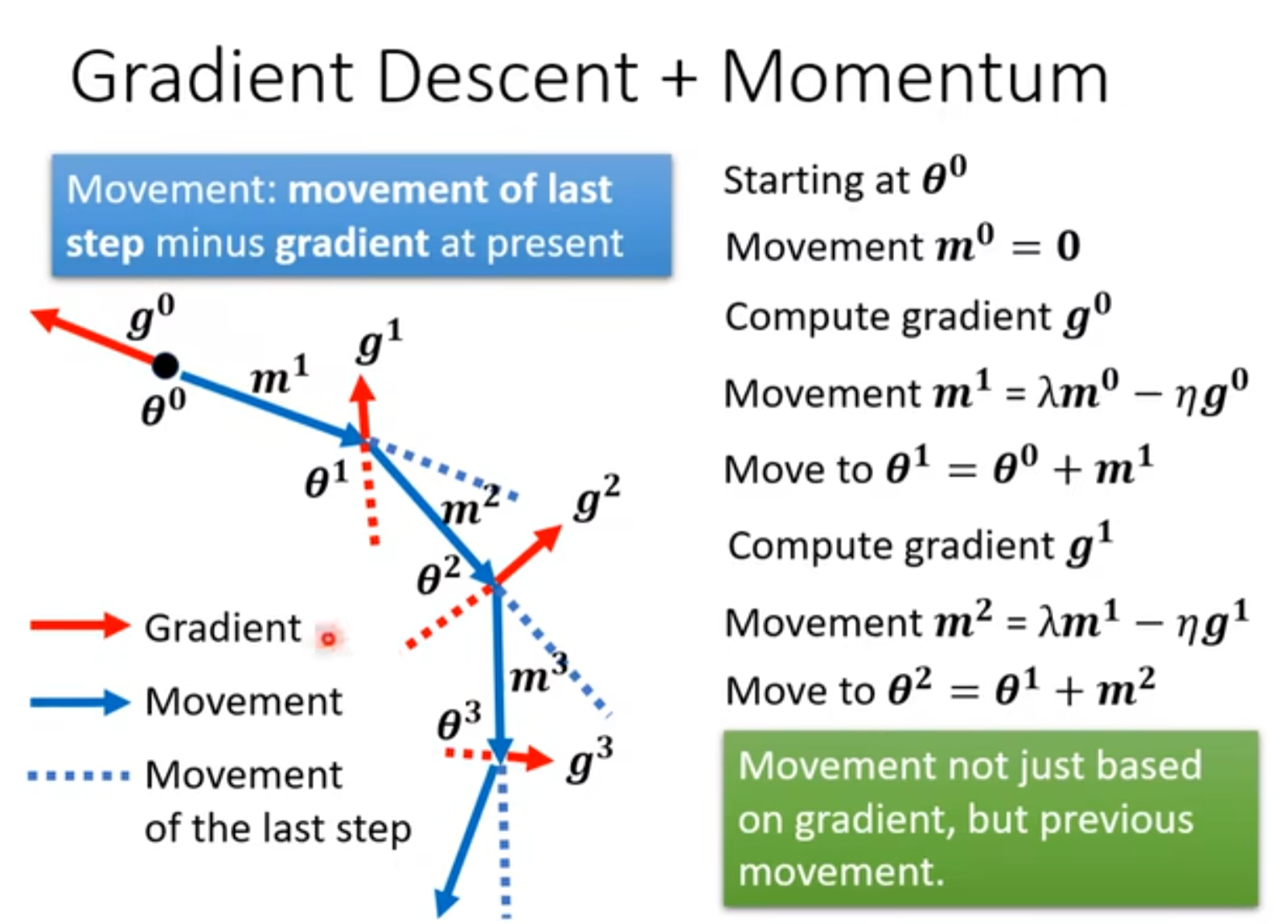
三.Momentum动量
![image]()
![image]()
critical points:梯度为0,saddle point和local minima
- 可通过海塞矩阵判断。
- 可沿海塞矩阵的特征向量方向逃离鞍点。
- local minima稀少
- 小批量和动量帮助逃离critical points。
四.adaptive learning rate
为每个参数设置不同的learning rate!
![image]()
![image]()
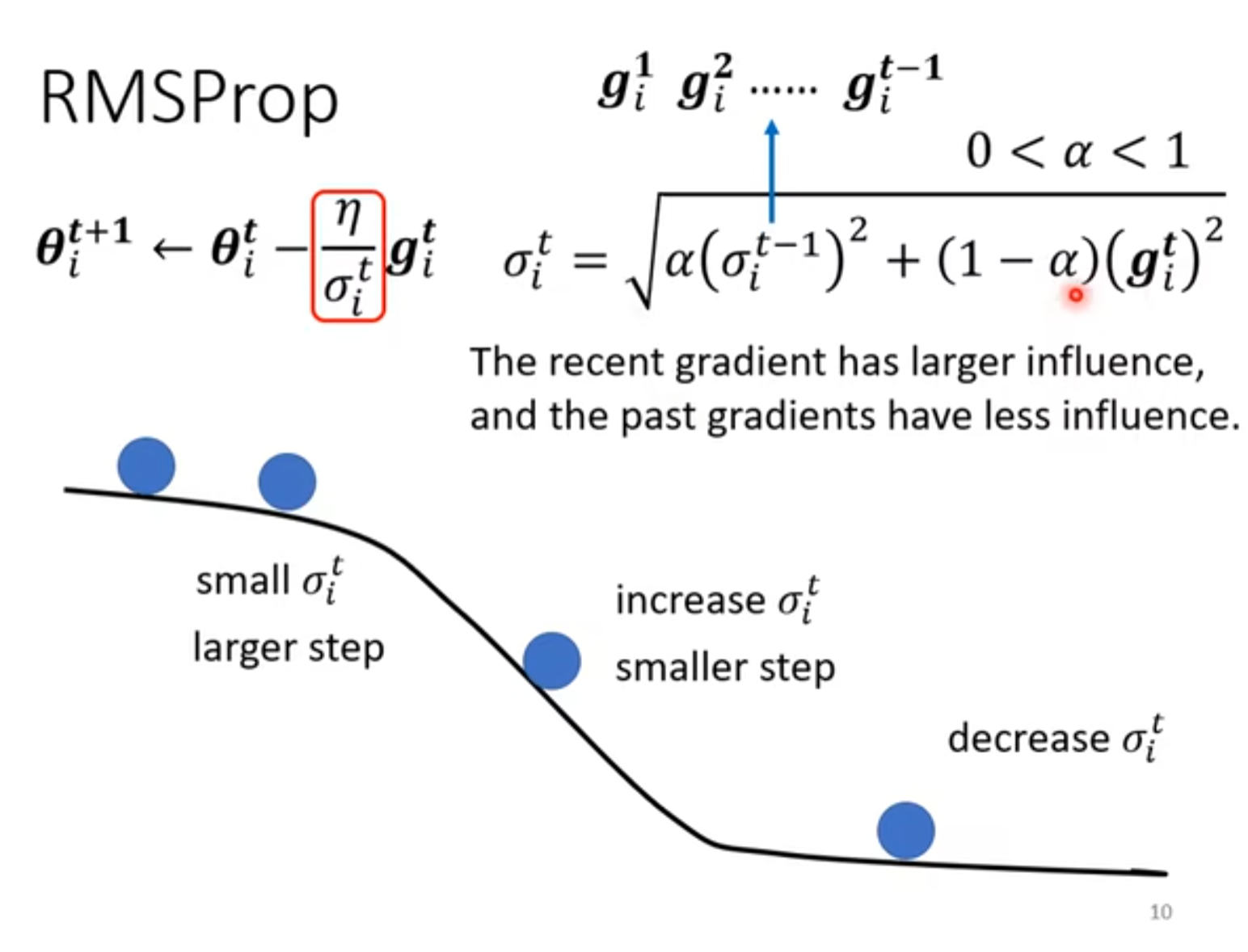
下方的曲线和蓝色圆点展示了 **σit如何影响学习步长 **:
- 当σit较小时(如左侧区域):σitη会变大,步长更大,适合在梯度变化剧烈的区域快速下降;
- 当σit增大时(如中间区域):步长减小,避免在梯度平缓区域 “冲过头”;
- 当σit减小时(如右侧区域):步长适配收敛过程,确保稳定找到最优解。
![image]()
![image]()
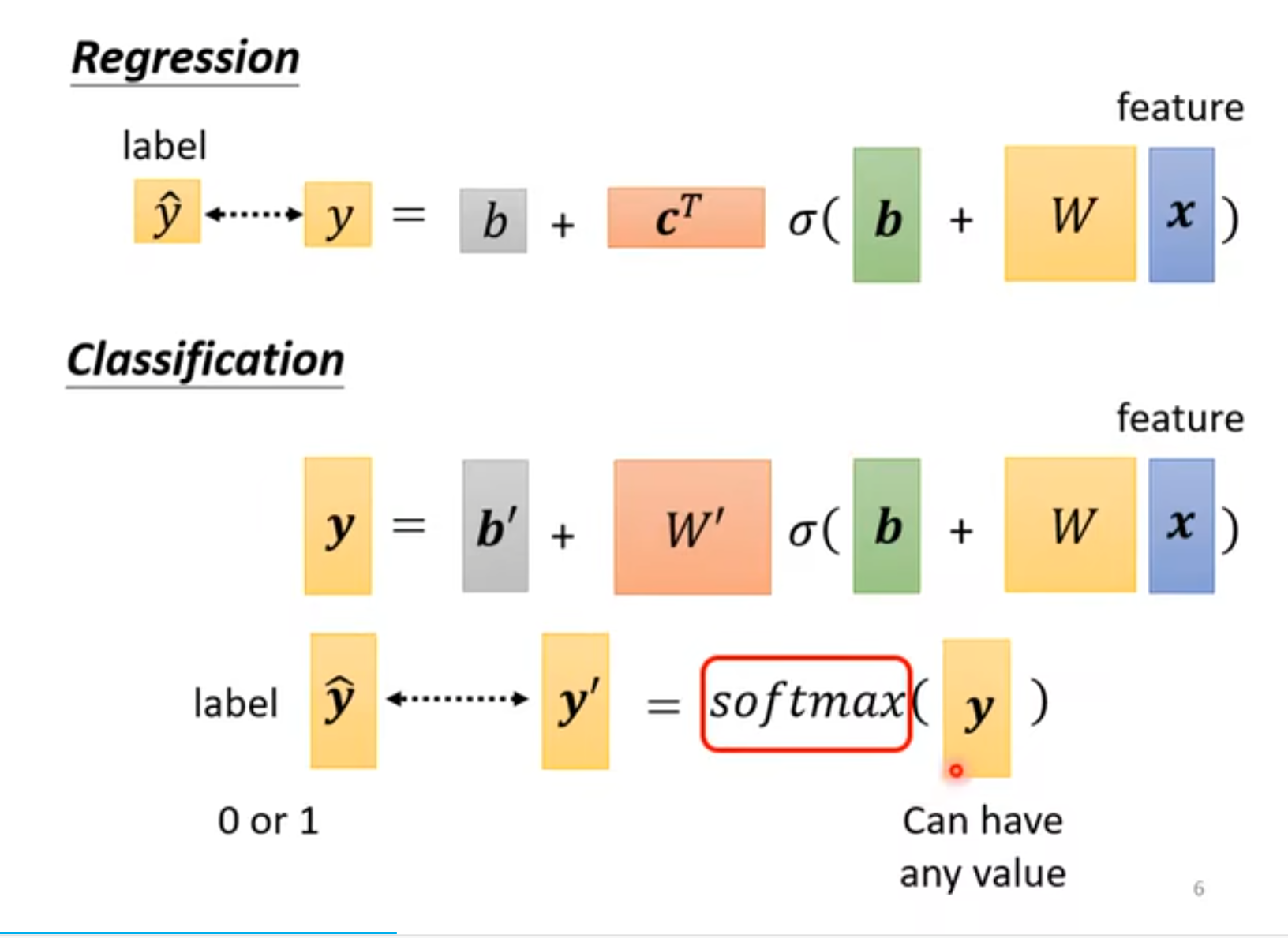
在分类任务中,交叉熵损失(Cross-entropy)比均方误差(MSE)更适合,原因如下:
- 分类任务的输出通常是经过
softmax的概率分布(表示对各类别的置信度),真实标签是one-hot 编码(仅正确类别为 1,其余为 0)。
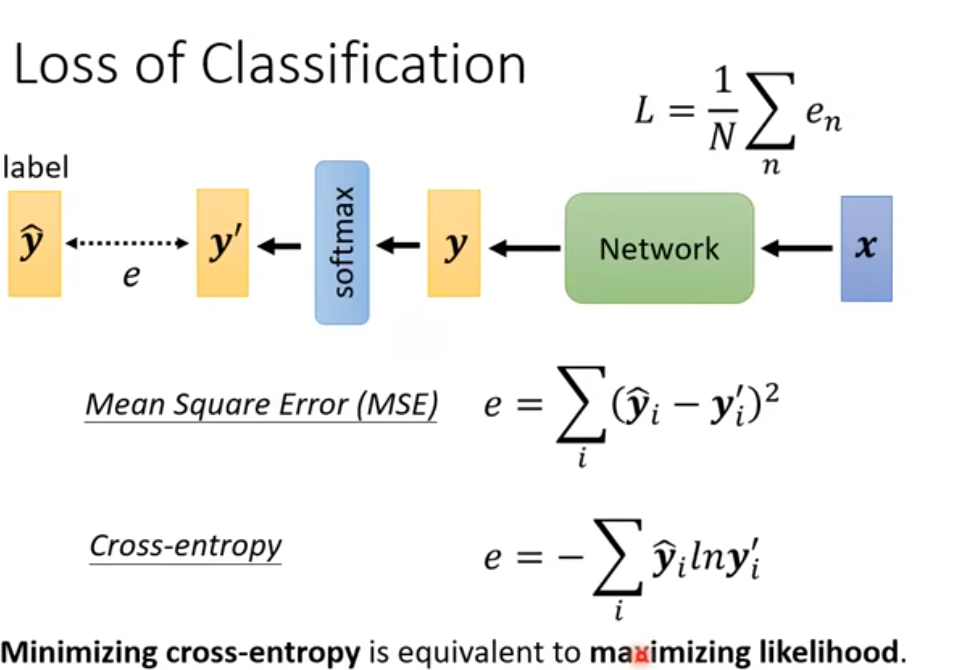
- 交叉熵直接针对 “概率分布的相似度” 优化,公式为 e=−∑iy^ilnyi′(因y^是 one-hot,实际等价于 −ln(y正确类别′)),其本质是极大似然估计,直接优化模型对 “正确类别” 的概率置信度。
- MSE 是为回归任务设计的(最小化连续值预测与真实值的平方差),分类任务中真实标签是离散的 “类别标识”,用 MSE 优化概率分布会出现适配性问题。
- 交叉熵的梯度:若模型对正确类别预测的概率y正确类别′越小(预测错误越严重),梯度∂参数∂e越大,能快速推动模型调整参数,收敛更高效。
- MSE 的梯度:假设真实标签y^是 one-hot 向量,MSE 的梯度为 ∂y′∂e=2(y′−y^)。当预测概率与真实标签差距较大时,梯度可能因
softmax的饱和特性(概率趋近 0 或 1 时,导数趋近 0)而消失,导致模型收敛极慢。
综上,在分类任务中,交叉熵损失是更优的选择;而 MSE 更适合连续值的回归任务(如预测房价、温度等)。


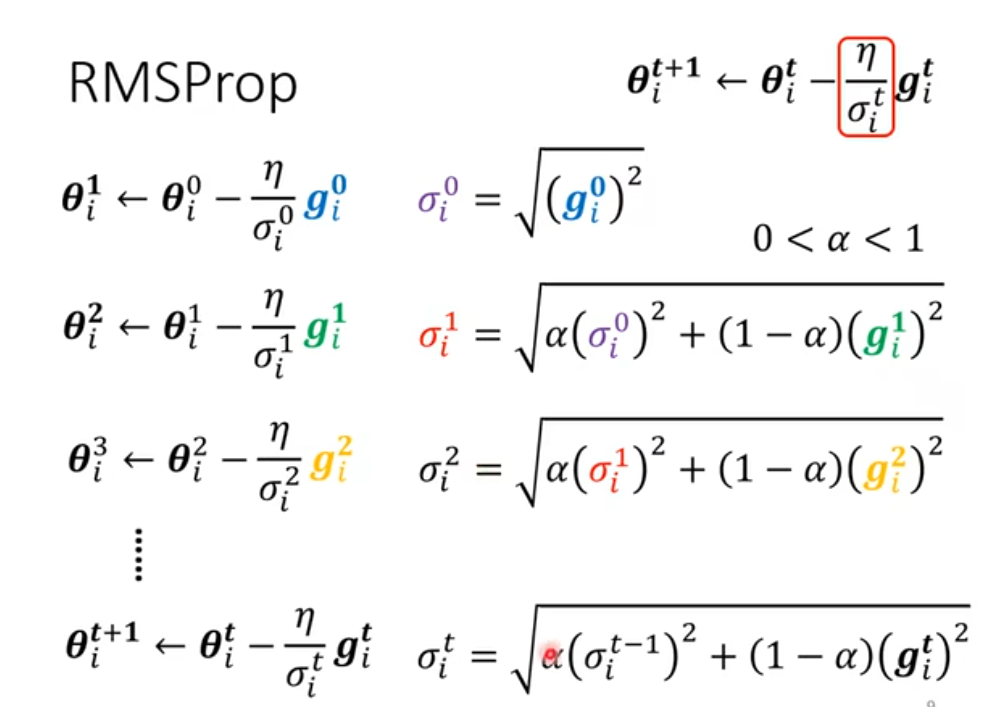
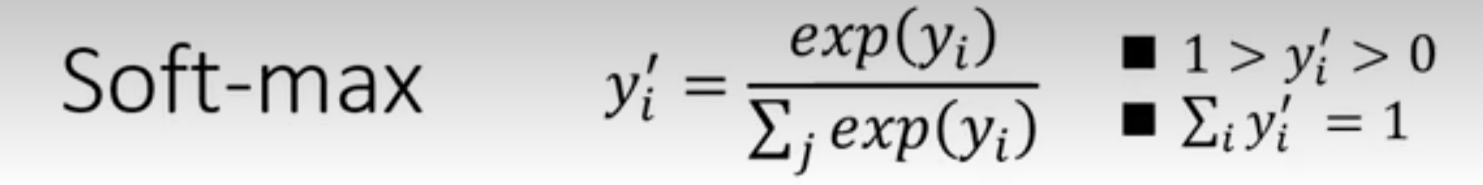









![[CISCN 2022 华东北]duck WP](http://pic.xiahunao.cn/[CISCN 2022 华东北]duck WP)









