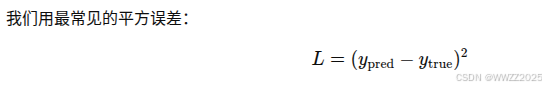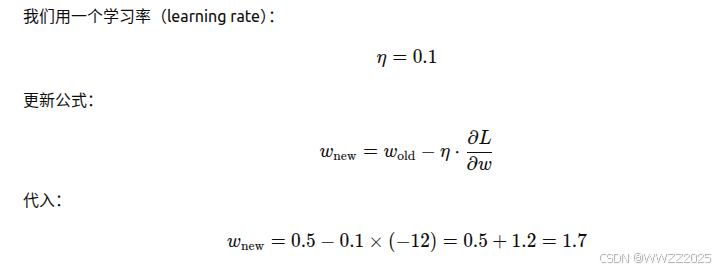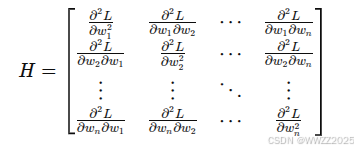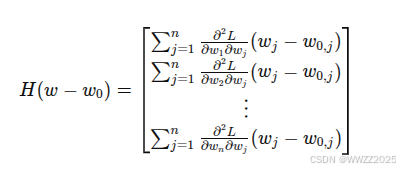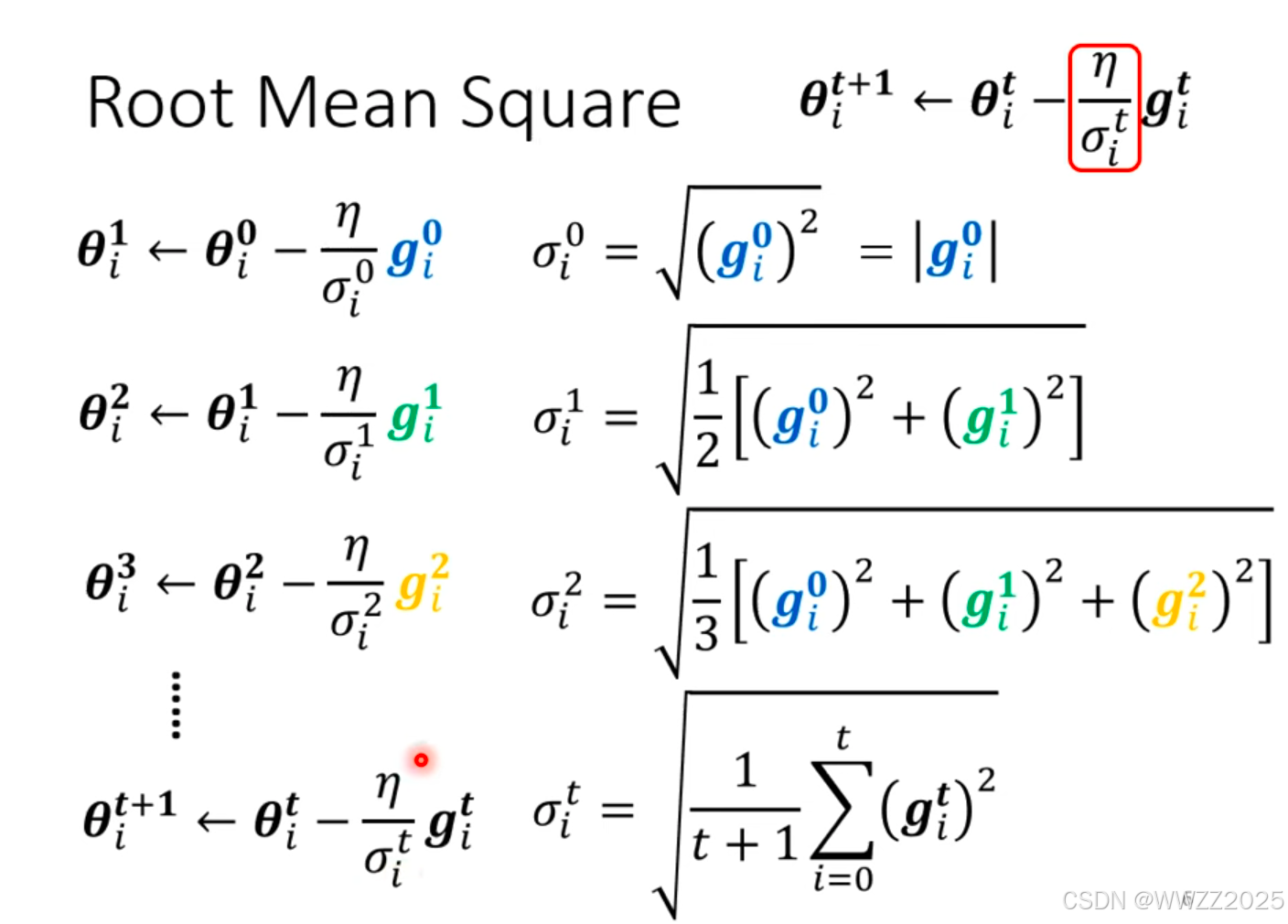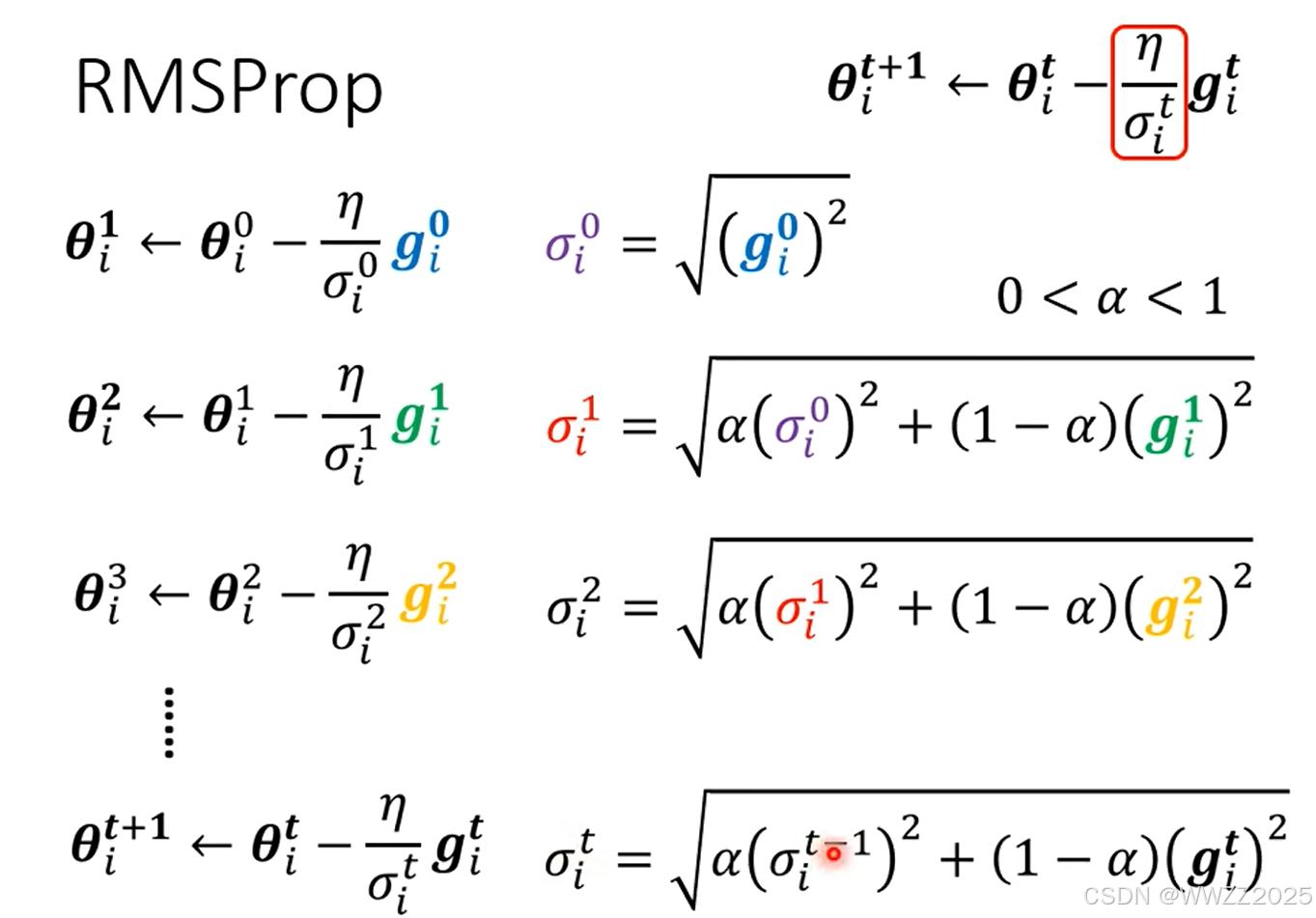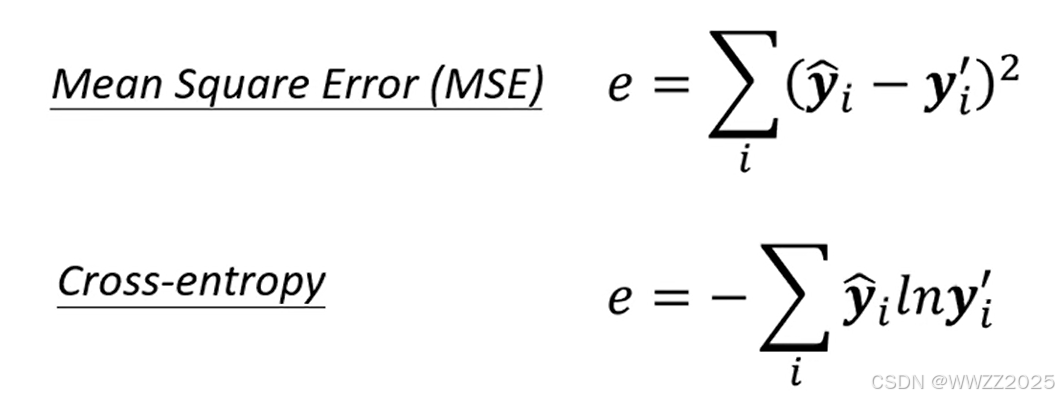快速上手大模型：深度学习1（初识、神经网络基础）

快速上手大模型：深度学习1（初识、神经网络基础） - 详解

目录
1 定义
2 核心原理
3 训练步骤
示例
4 深度学习与机器学习区别
5 训练攻略
5.1 临界点(critical point)
临界点判别
5.2 批次(batch)和动量(momentum)
5.2.1 批次
5.2.2 动量
5.3 自动调整学习率(Learning Rate)
5.4 损失函数选择(Loss)
理论部分根据李宏毅课程学习，整体深度学习部分还配合李沫的实践课程，详见标有“实践”部分的章节，理论部分课程链接：https://www.bilibili.com/video/BV1Bq421A74G/?spm_id_from=333.1391.0.0&p=40

1 定义

引子

AI科技对应的应用方向：
深度学习技术应用：
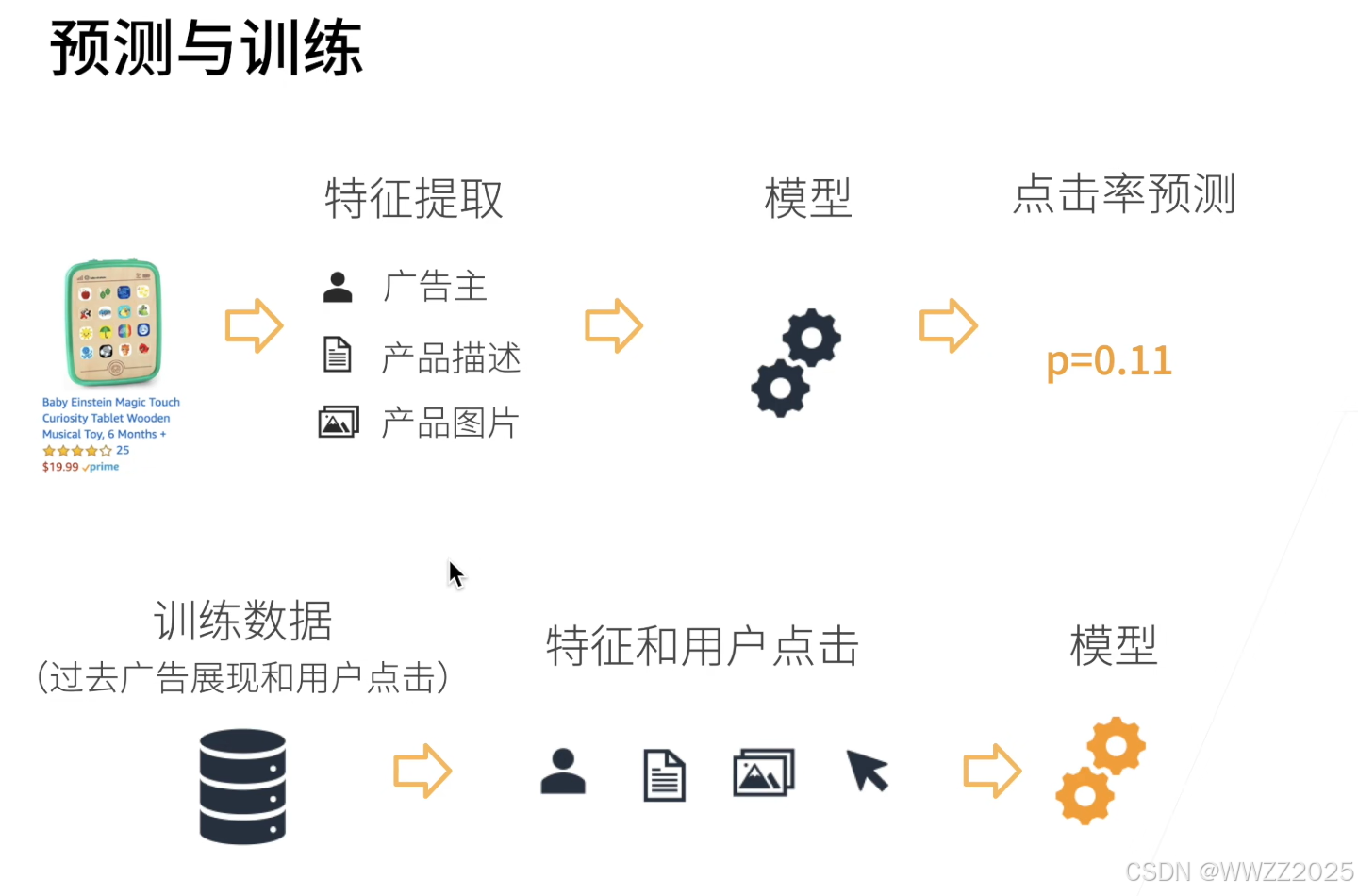
电商商品推荐，当用户搜索目标商品时，后台会根据客户搜索的词条找到商城中所有个这个词条相关的商品，接着进行特征提取(此处为广告主、产品描述、产品图片)，将特征提取放入模型进行训练，得到预测的客户可能点击的概率，用户页面看到的商品排序为预测的点击率*平台对该链接的提成。
该案例中预估的点击率由过去一段时间广告展现和用户真实点击情况训练得来。

深度学习（Deep Learning）是一种让神经网络通过大量数据和反向传播算法自动学习特征、优化权重，从而实现感知、理解和生成能力的人工智能方法。
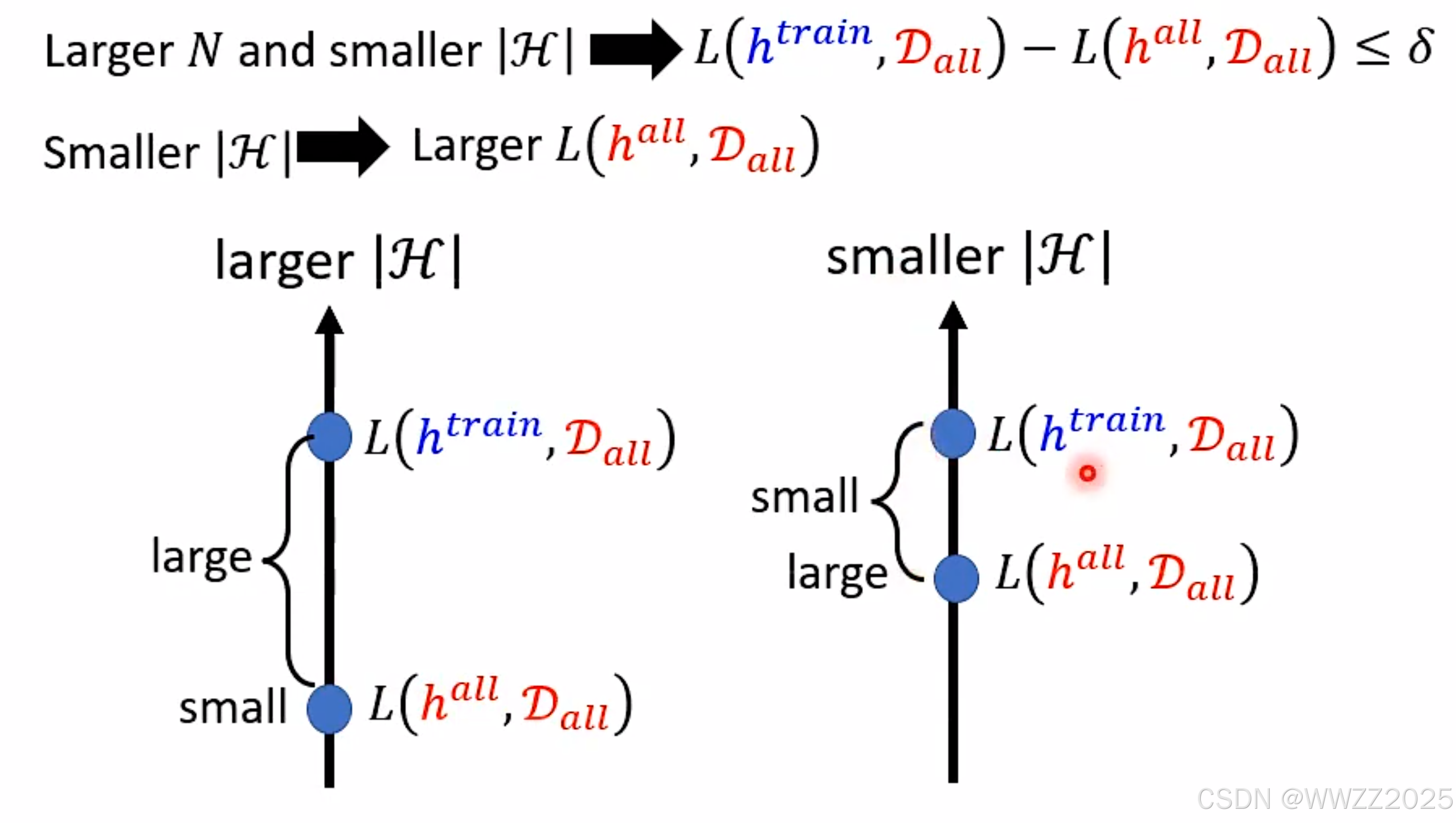
PS.深度学习许可解决模型复杂度H与训练集L(h-trian,D-all)的冲突问题，这是机器学习所不能的。

2 核心原理

多层神经网络（deep neural network），大致结构为：
输入层 $\rightarrow$ 隐藏层1 $\rightarrow$ 隐藏层2 $\rightarrow$ ... $\rightarrow$ 隐藏层n $\rightarrow$ 输出层
PS.理论上隐藏层越多预测值与实际值越接近，但过多可能存在过拟合情况。

3 训练步骤

（1）把输入信息喂进网络，算出输出；
（2）计算预测结果与真实答案的差距（loss）；
（3）用反向传播（backpropagation）算出每个权重对 loss 的影响；
（4）用梯度下降（gradient descent）更新权重，让 loss 变小一点。
路线： $\eta \frac{\partial L}{\partial w}- w\rightarrow w$
其中 $\eta$ 为学习率， $\frac{\partial L}{\partial w}$ 为 loss 对权重的梯度，过程中迭代多次，直到网络学会。
为了防止过于依赖训练集中数据降loss，导致用于测试时在测试数据集上效果不佳。就是PS.素材集需要分成三个部分：训练集(Training Set)、验证集(Validation Set)、测试集(Test Set)，验证集

示例

4 深度学习与机器学习区别

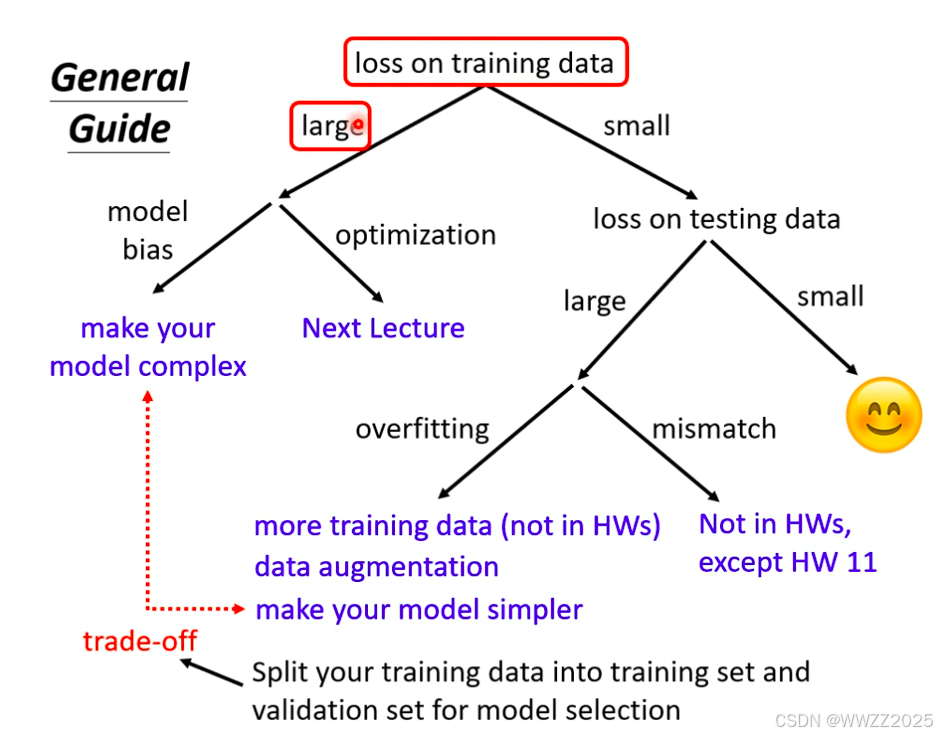
5 训练攻略

（1）检查训练数据集的损失loss
如果损失偏大，可能是模型偏差(model bias)、优化(optimization)做得不好。
a.模型偏差可以增加特征值 $_{}$ $w_{i}$ ；
b.优化没做好（训练loss大，一直降不下来）允许试着调学习率（学习率小会导致 loss 下降
很慢、几乎不变，此时学习率*10；大导致 loss 上下震荡、不收敛，此时学习率➗10）、
初始化、优化器。
如果损失偏小，但测试数据集损失偏大，可能过拟合(overfitting)、不匹配(mismatch)
a.过拟合可以增加训练样本、运用数据增强(Data augmentation)技术、提前限制训练模型（如二次曲线等，限制模型常用方式有：给较少参数、减少特征值、提前结束模型预测、正则化、辍学dropout）
b.不匹配能够通过避免人为数据误用（训练数据集应用A，测试数据使用B）、提高模型泛化能力（使用正则化、dropout、batchnorm、数据增强、pretraining、ensemble、early stopping 等方法）

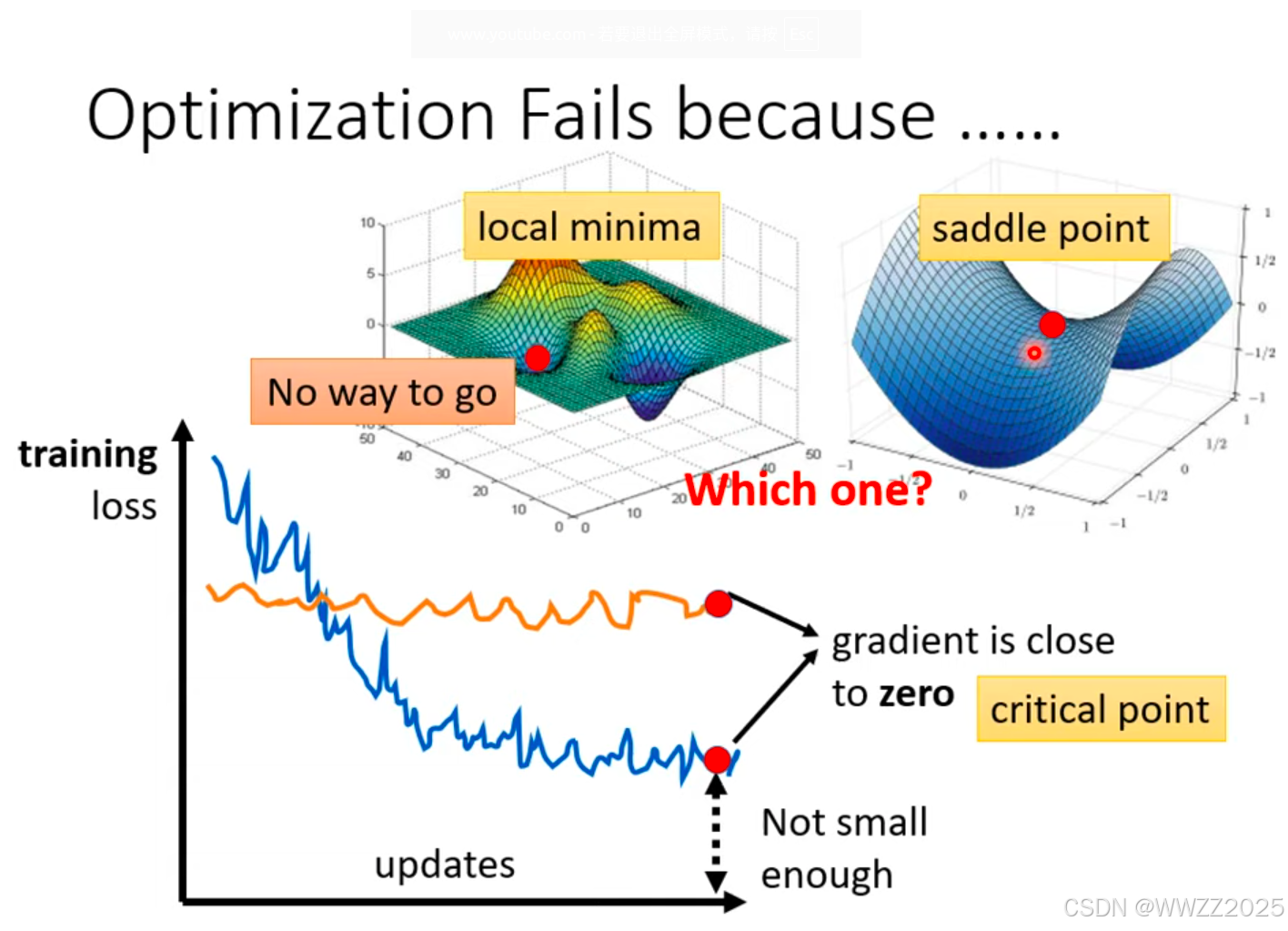
5.1 临界点(critical point)

临界点分为局部最小值(local minima)和鞍点(saddle point)，这两个区分如下。

临界点判别

泰勒级数近似(Taylor Series Approximation)：
$L(w )\approx L(w_{0})+(w-w_{0})^{T}\bigtriangledown L(w_{0})+\frac{1}{2}(w-w_{0})^{T}H(w-w_{0})$ ，其中符号含义如下，注意损失函数L为矩阵形式。
判别：
（1） $\frac{1}{2}(w-w_{0})^{T}H(w-w_{0})> 0$ ，局部最小(Local minima)；
（2） $\frac{1}{2}(w-w_{0})^{T}H(w-w_{0})< 0$ ，局部最大(Local maxima)；
（3）有时 $\frac{1}{2}(w-w_{0})^{T}H(w-w_{0})> 0$ ，有时 $\frac{1}{2}(w-w_{0})^{T}H(w-w_{0})< 0$ ，鞍点(saddle point)。

5.2 批次(batch)和动量(momentum)

5.2.1 批次

批次：在训练神经网络时，一次拿多少数据来更新参数。
（1）有无批次比较
假设20个样本，左图在看完所有样本后输出损失函数L，进而运算 $\eta \frac{\partial L}{\partial w}- w\rightarrow w$ ；右图设置批次1，每次批次后输出损失函数L，循环20次，该法存在噪声，两者要求时间不一定，详见（2）耗时比较。
结论：
分批次可能提高效率；一个批次的平均梯度允许在准确性和速度之间取得平衡；泛化性好。
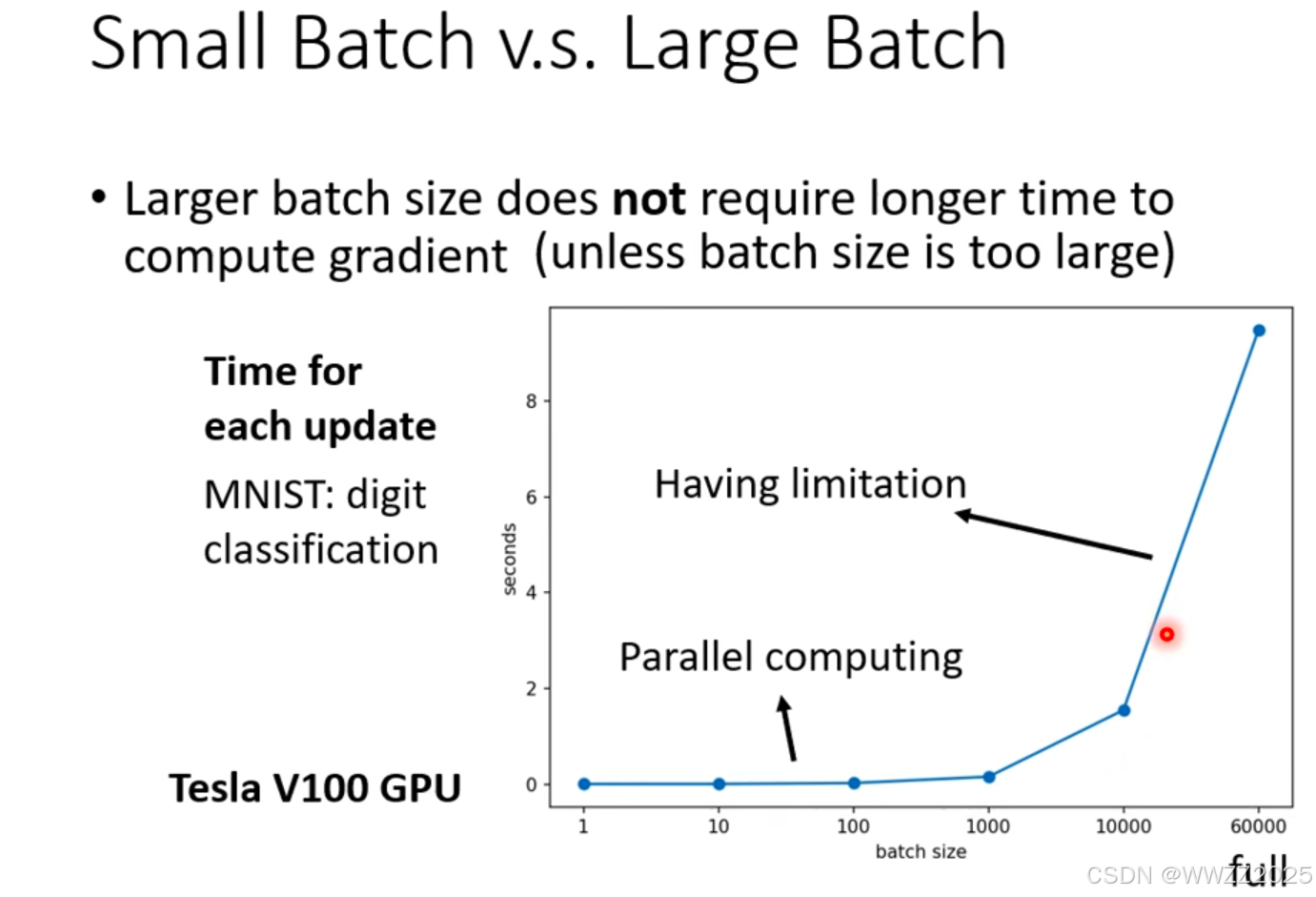
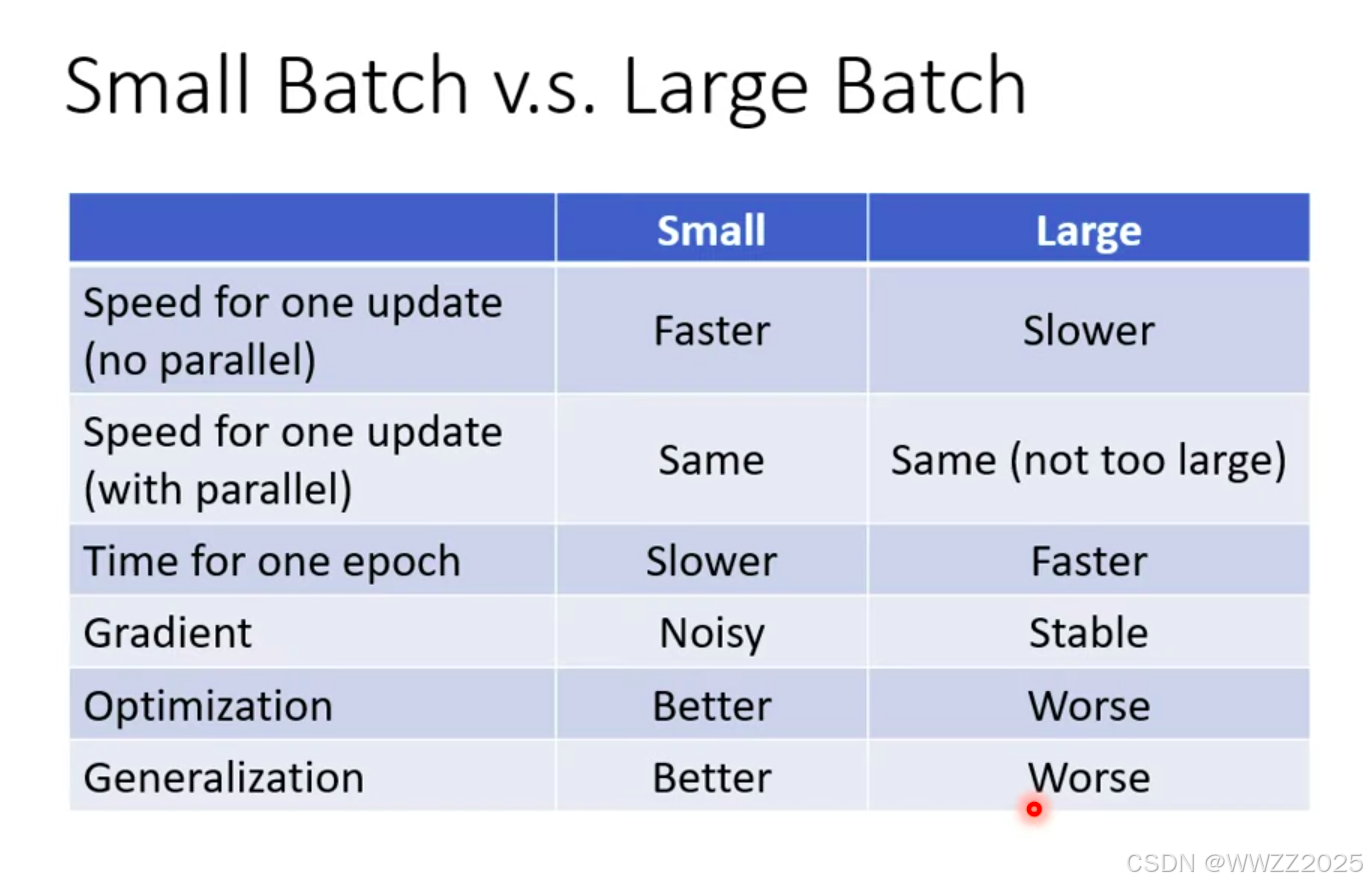
（2）大、小批次耗时比较
结论：
当一个批次样本数据小于1000时，运算时间基础差不多，随着一个批次样本数据量的增加，运算时间增加。
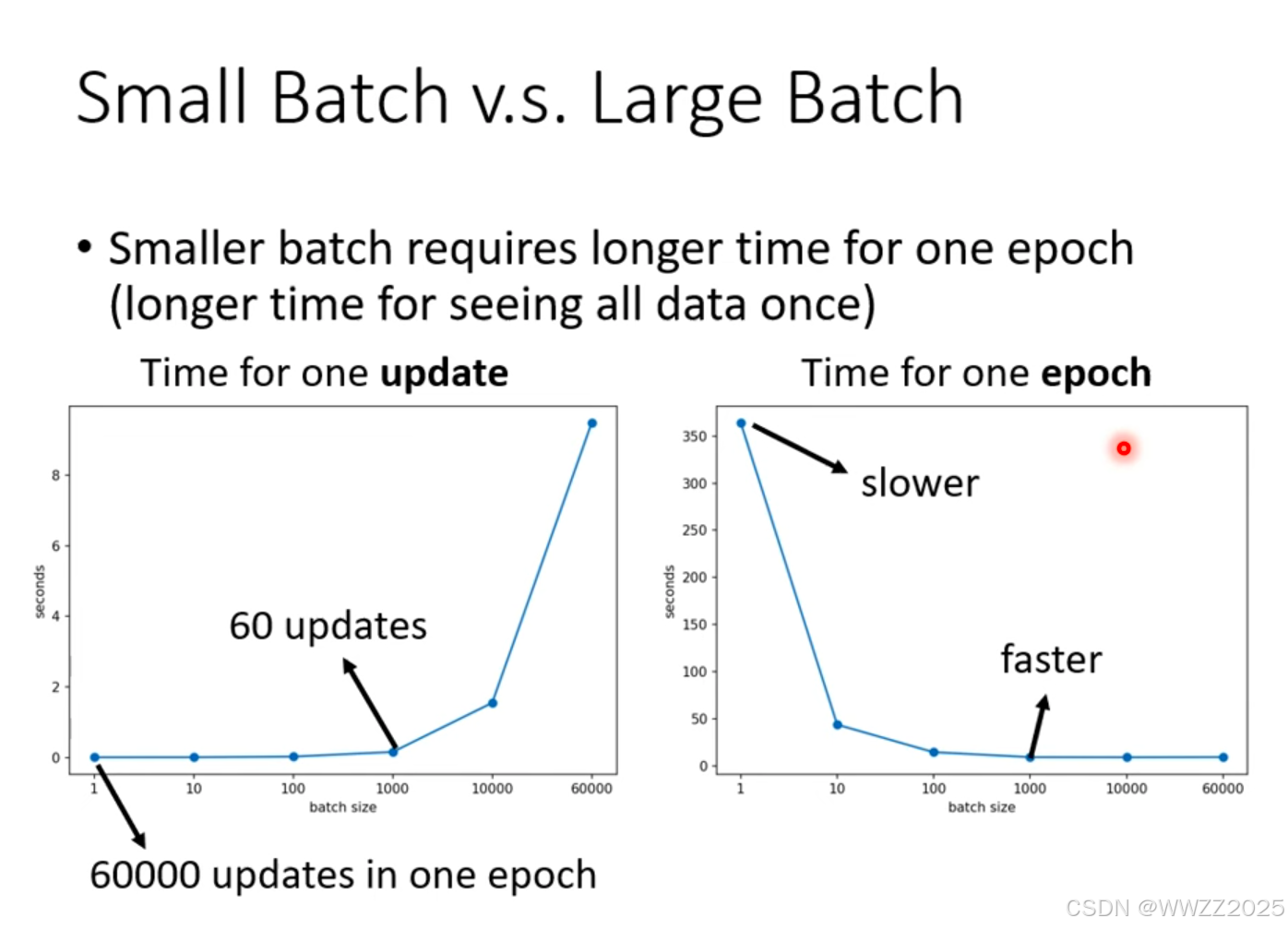
（3）跑完一个整体样本(epoch)耗时比较
结论：
在并行运算时，大样本批次整体样本跑下来的耗时反而低。
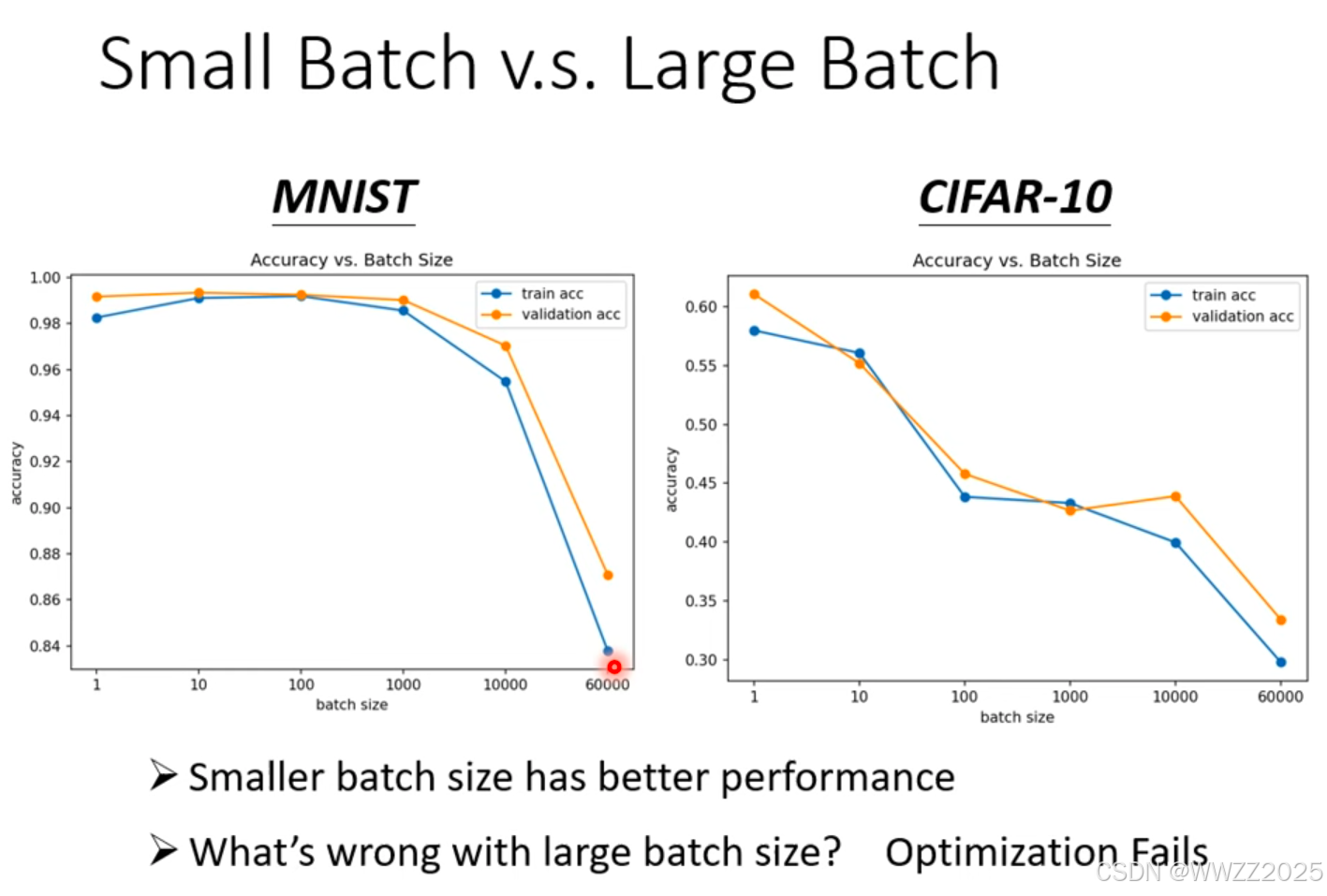
（4）大、小批次训练出来的预测精度比较
结论：
大样本批次训练出来的精度会降低，是优化的障碍。
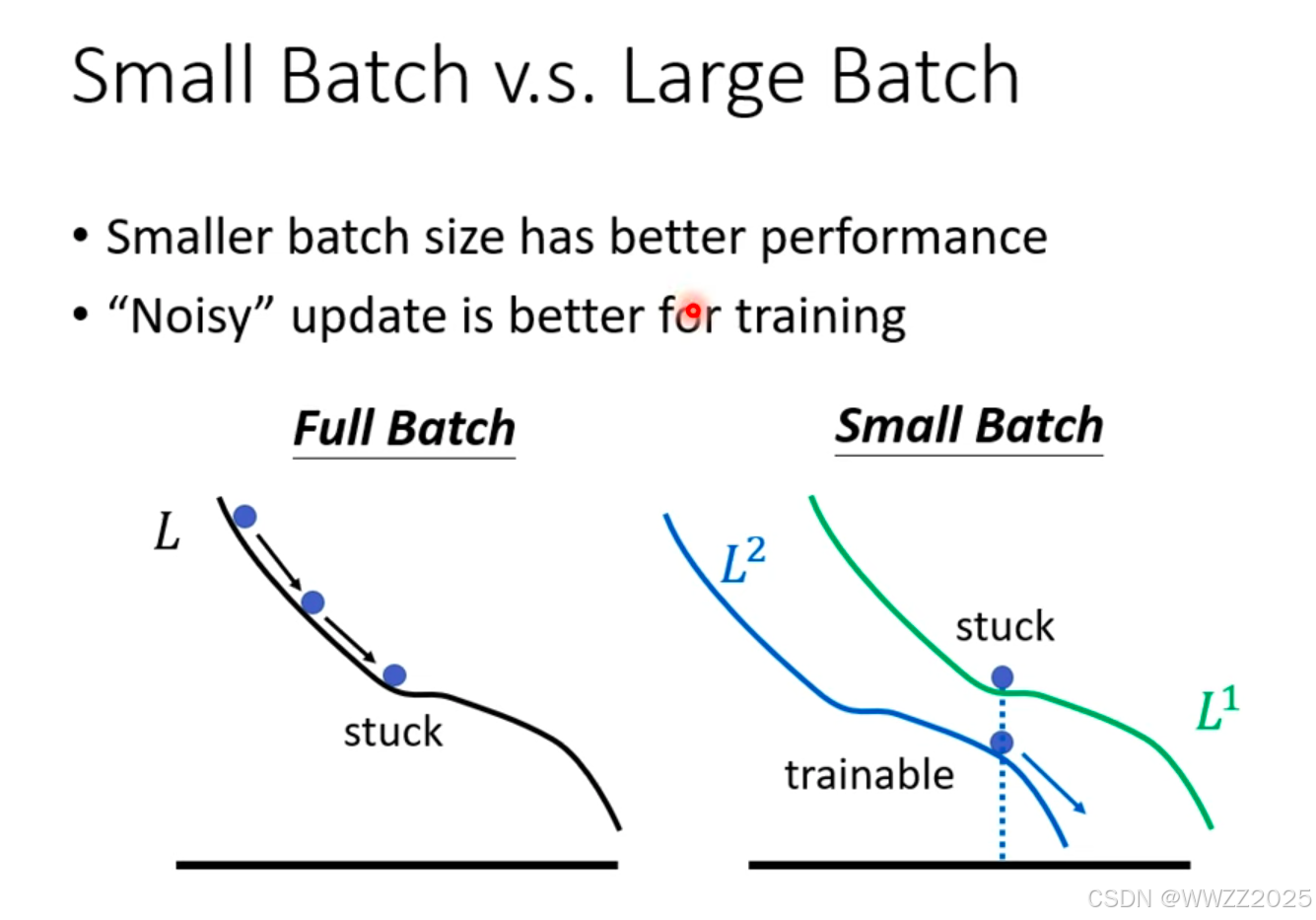
原因：
小样本批次存在噪声(Noisy)，L1中找到的最小值在L2中不一定是最小，在L2中还能继续找最小。
总结：
a.单次运算无并行时，小样本批次运算更快；
b.单次运算有并行时，大、小样本批次运算差不多；
c.整体样本运算是，大样本批次运算更快；
d.小样本批次梯度下降时存在噪声，大样本批次比较稳定；
e.小样本批次优化效果更好；
f.小样本批次在测试样本中效果更好。

5.2.2 动量

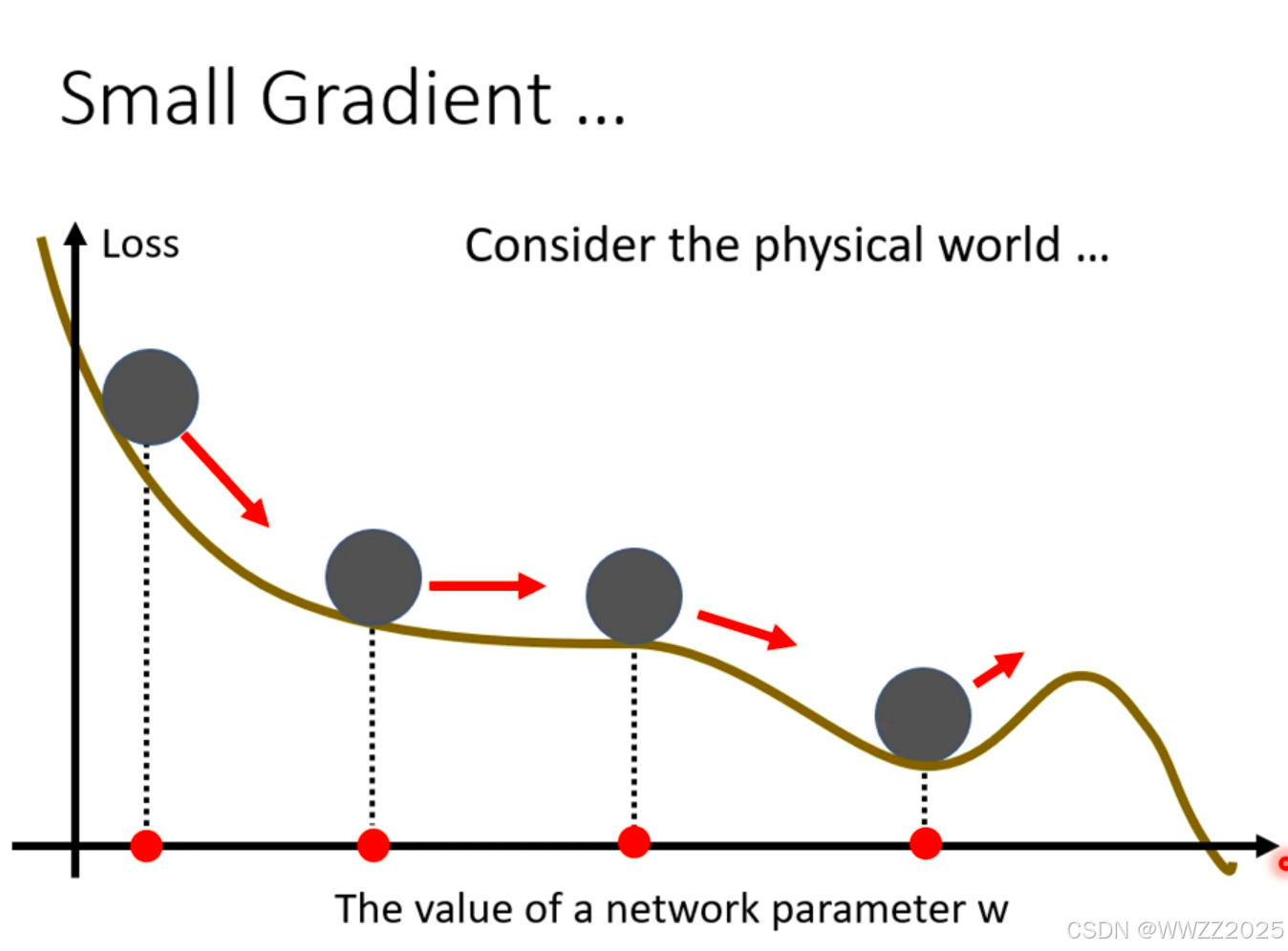
（1）引子
物理世界中小球从高处下降，遇到小坡因动能惯性会冲出小坡继续下降，将该原理引入深度学习。
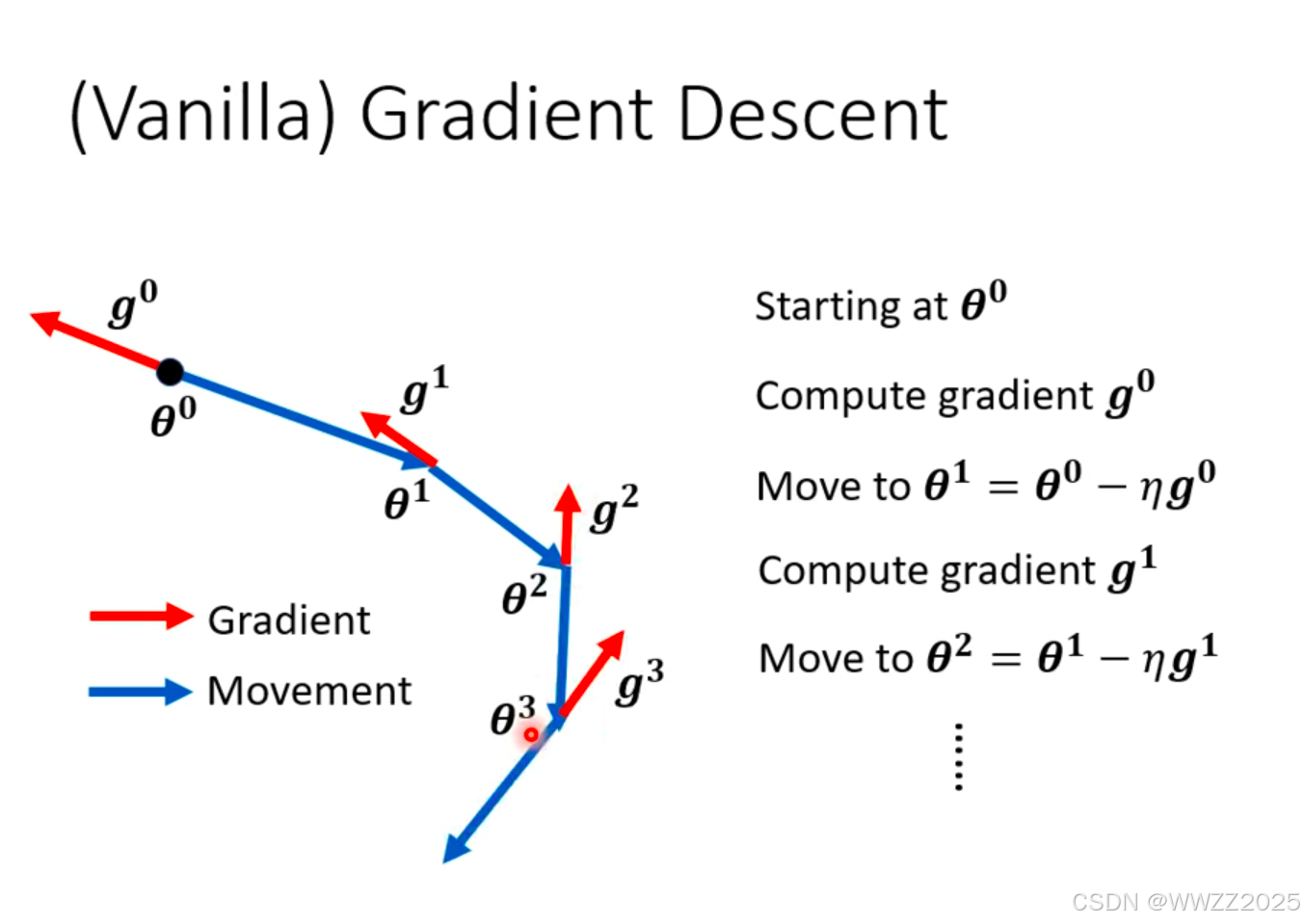
（2）梯度下降原理
梯度下降时，沿着梯度运算的反方向运动，如图蓝色线。
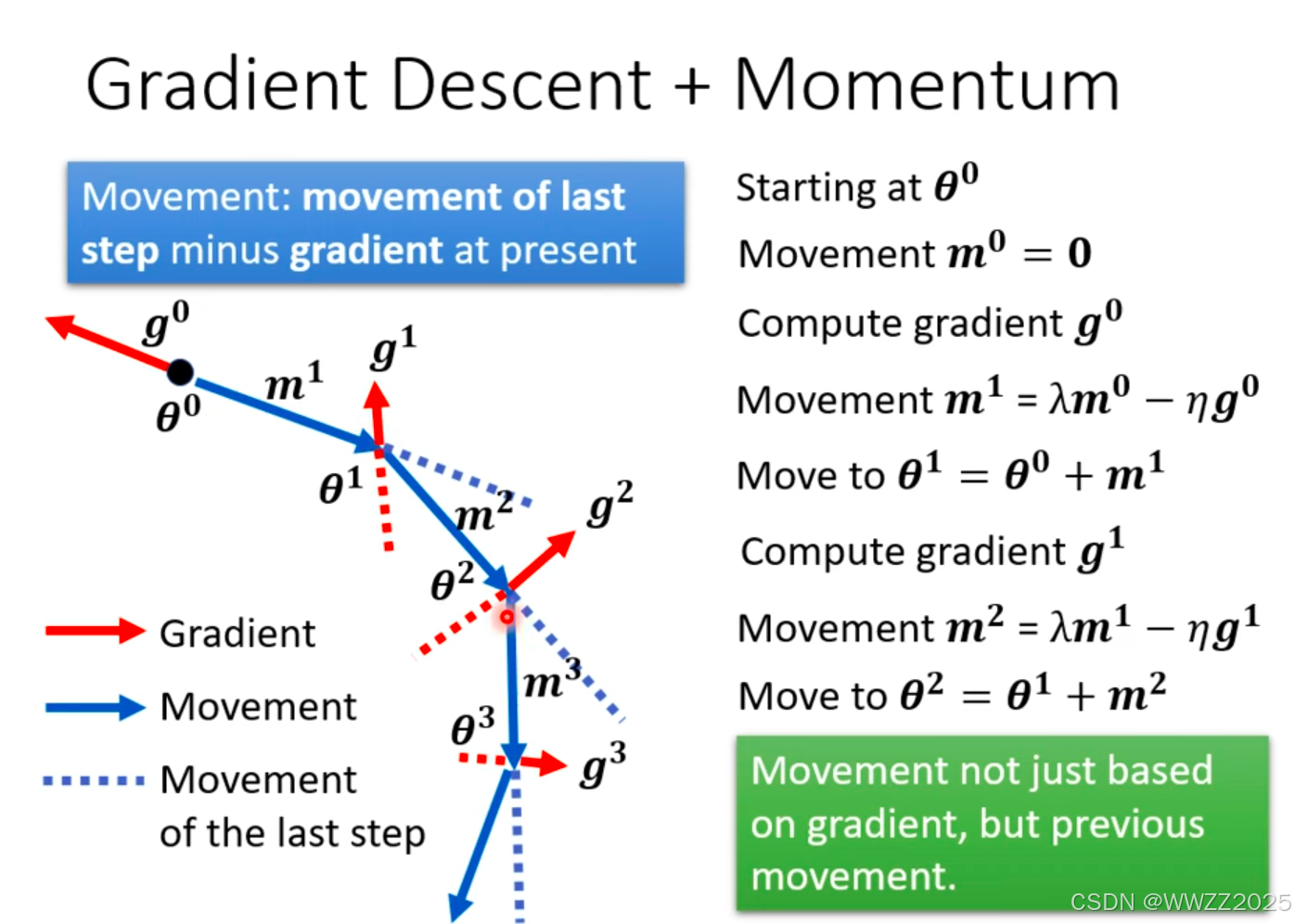
（3）梯度下降+动量
因动量的加入，梯度运动不再仅受梯度下降方向影响，还和上一时刻动量方向有关，实际梯度走向为梯度方向+上一时刻动量方向之和，如图蓝色实线。

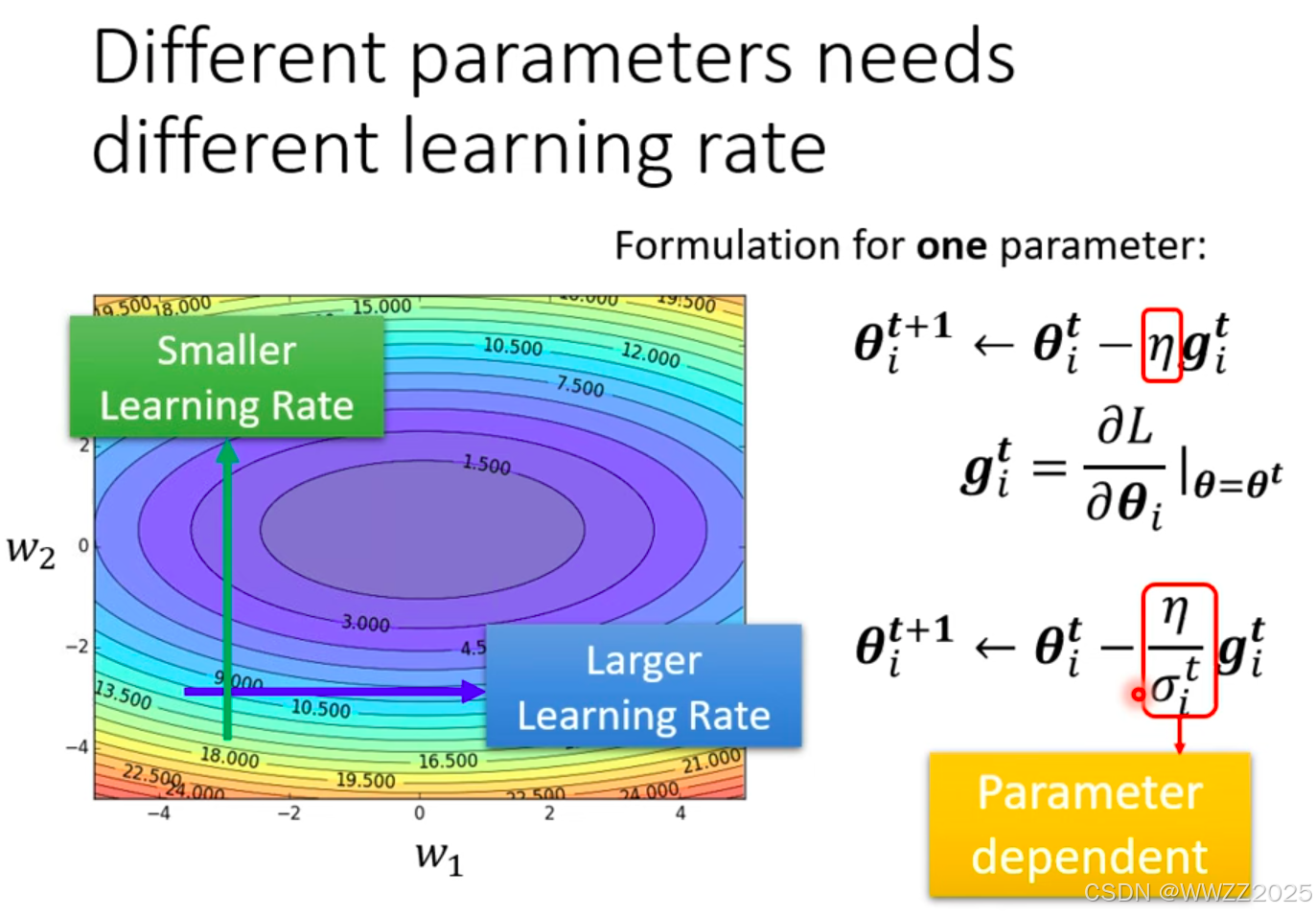
5.3 自动调整学习率(Learning Rate)

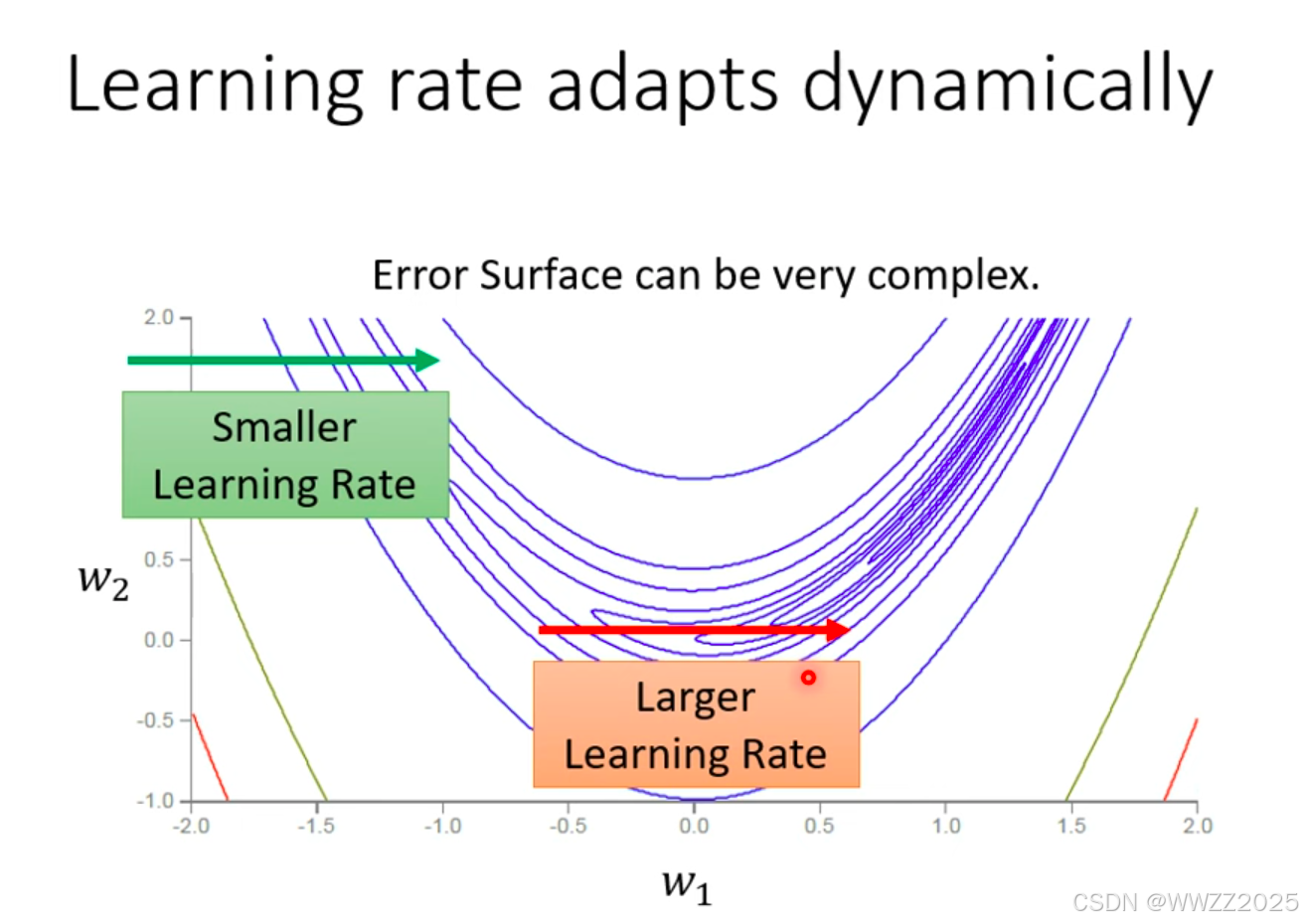
训练时利用固定的学习率会导致梯度降不下去，因此在某一方向上梯度下降值很小（平坦），学习率调大一点；反之小一点。
学习率计算方法：
$g_{i}^{t}$ 为某一个参数时，第i次更新梯度下降（即求偏导）
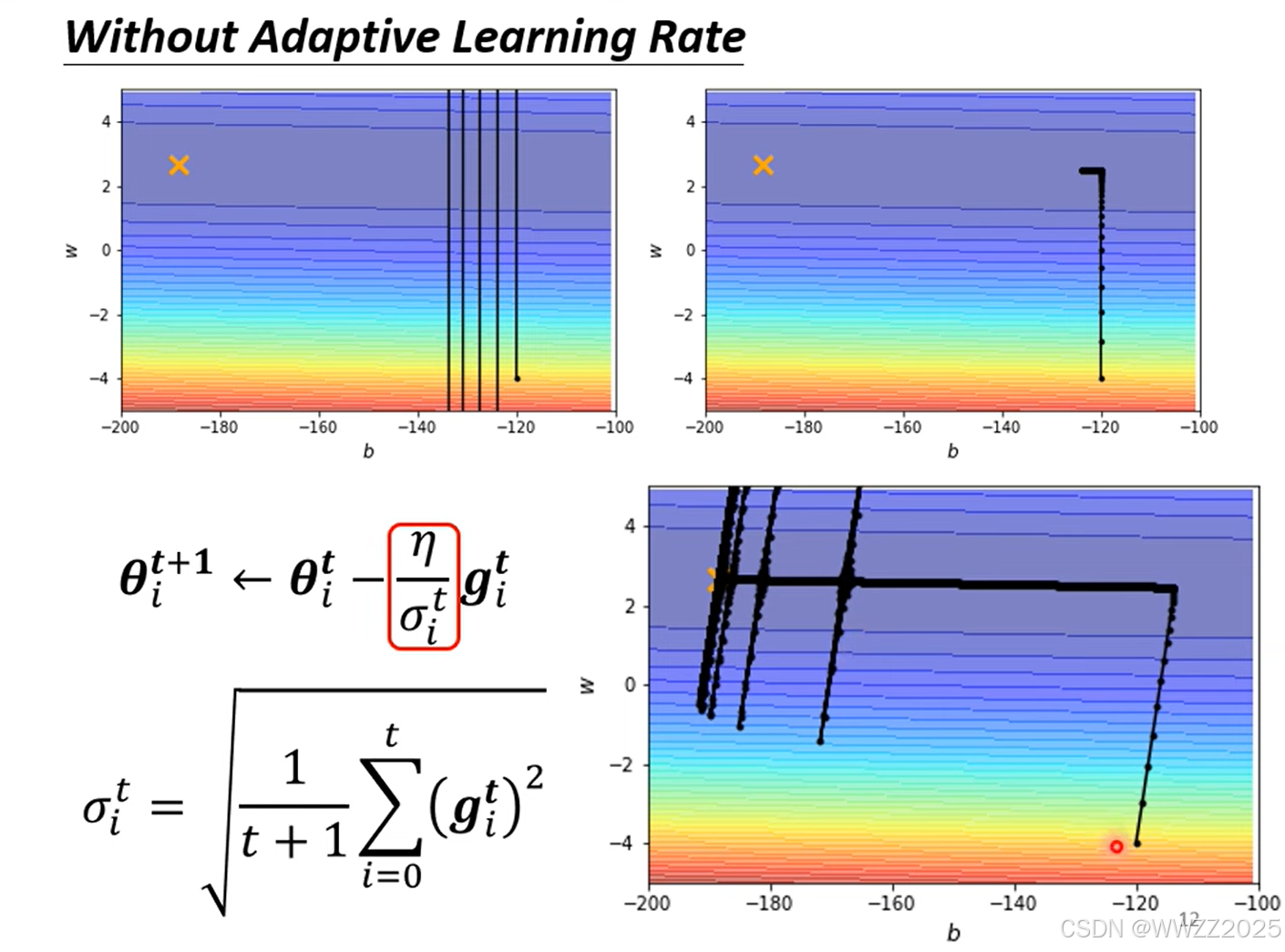
，在同方向上坡度仍有出入，绿线坡度陡峭，学习率需调小；红线坡度较平缓，学习率应较大，因此采用就是但RMSProp法：
目前Optimzer常用策略是Adam:RMSProp+Momentum，但是该方案会出现下图所示在平缓区间向陡坡运动趋势，但经过不断迭代仍会回到缓坡。
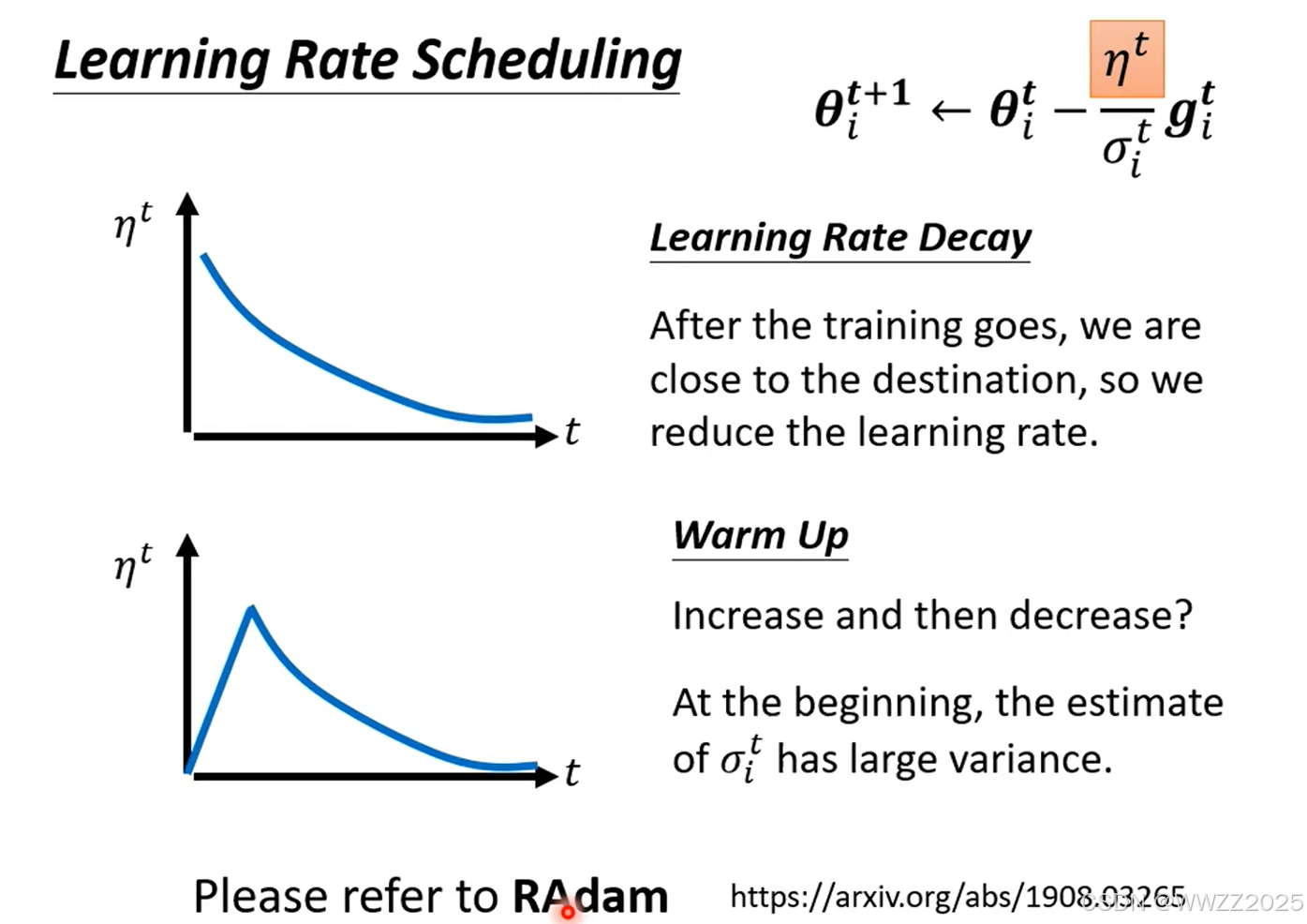
为避免出现该情况，可以通过调整 $\eta$ ，常用方法有学习率衰减(Learning Rate Decay)，其随着时间逐渐减小；还可以用预热(Warm Up)，其随着时间先大后小。

5.4 损失函数选择(Loss)

两个都是常用优化问题，MSE（均方误差）适用于回归挑战、训练连续数值，Cross-entropy（交叉熵）适用于分类问题。
交叉熵
（1）原理
该技巧用于分类，衡量两个分布之间的差距，L算出来值越小，说明预测越准确
（2）公式
$L=-\sum_{i=1}^{n}y_{i}log(\hat{y}^{i})$ ，其中累加位置表示一共有多少个类别（比如区分猫、狗、猪，那此时n=3）， $y_{i}$ 是样本数据真实情况（0为假，1为真）， $\hat{y}^{i}$ 为预测的样本数据概率（0-1之间）。
PS.深度学习中一般以ln为底，不影响结果相对大小。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/973676.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

完整教程：【AI智能体】Coze 打造励志图文智能体应用实战操作详解

完整教程：【AI智能体】Coze 打造励志图文智能体应用实战操作详解2025-11-23 08:46 tlnshuju 阅读(0) 评论(0) 收藏举报pre { white-space: pre !important; word-wrap: normal !important; overflow-x: auto !im…