题意:给出 \(n,P\),现在问对于所有 \(n\) 个点且父亲编号小于儿子的树,对其进行 dfs 并且优先遍历编号小的子节点,问有多少种 dfs 序。对 \(P\) 取模。\(n\le 800\)。
做法:
首先考虑如何判定一种 dfs 序是否合法。考虑一个贪心策略,我维护一个深搜栈,考虑加入一个点 \(u\),为了保证父亲和已经遍历的兄弟小于 \(u\),从栈顶轮流弹直到弹出了一个比 \(u\) 小的数。如果弹完了就无解。
这样我们就用一个 dfs 序对应了唯一一颗树。
但是用这个贪心过程做 dp 不是很方便,原因是我们需要记录一条链的节点编号才行。我们考虑用这个贪心去刻画这样的树的性质。
我们考虑有小于关系的我们就连一条从小指向大的边,那么会转化成每个节点向自己的第一个儿子连一条边,然后兄弟之间前一个向后一个连边,如下图:
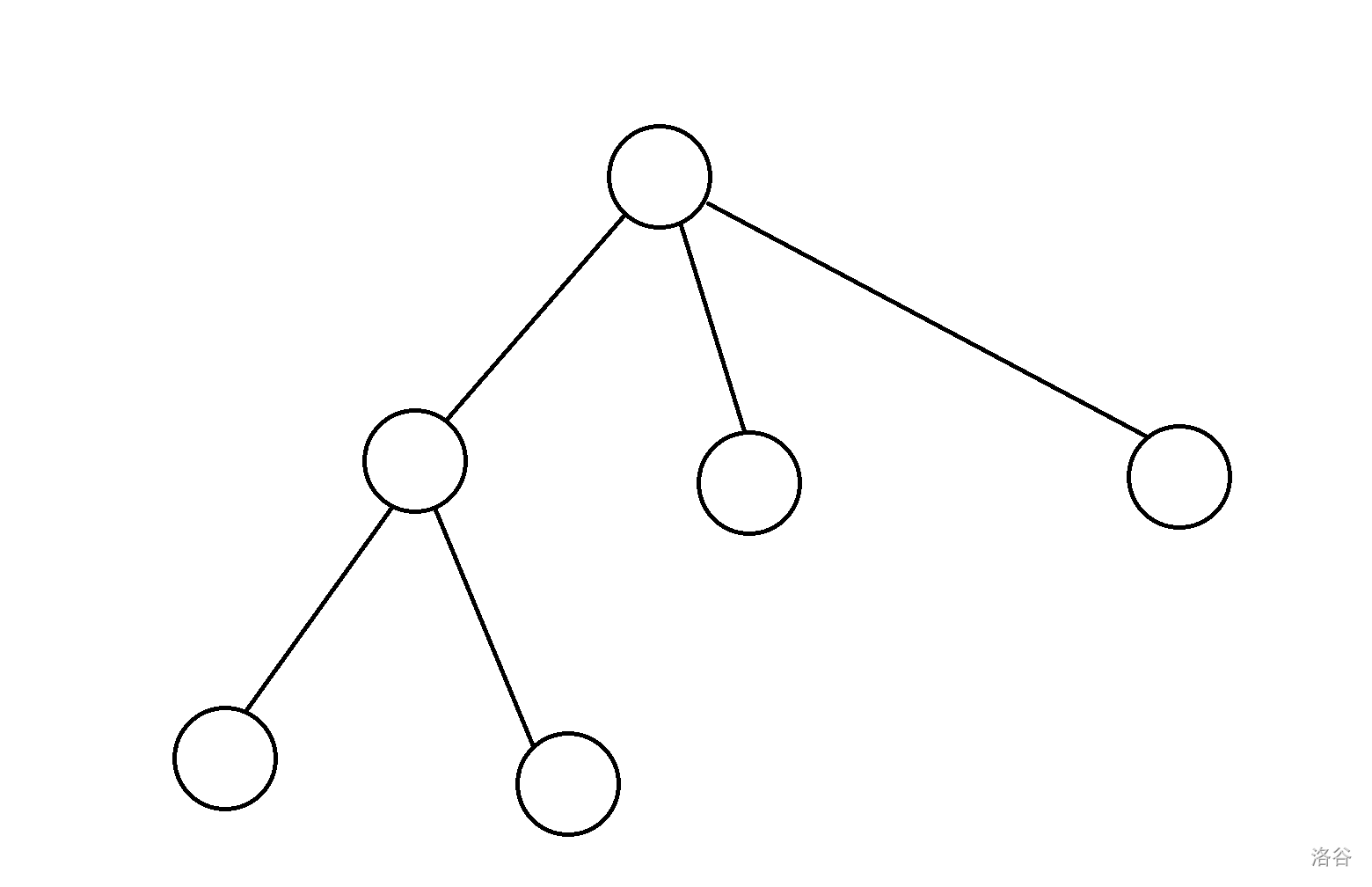
会改成:
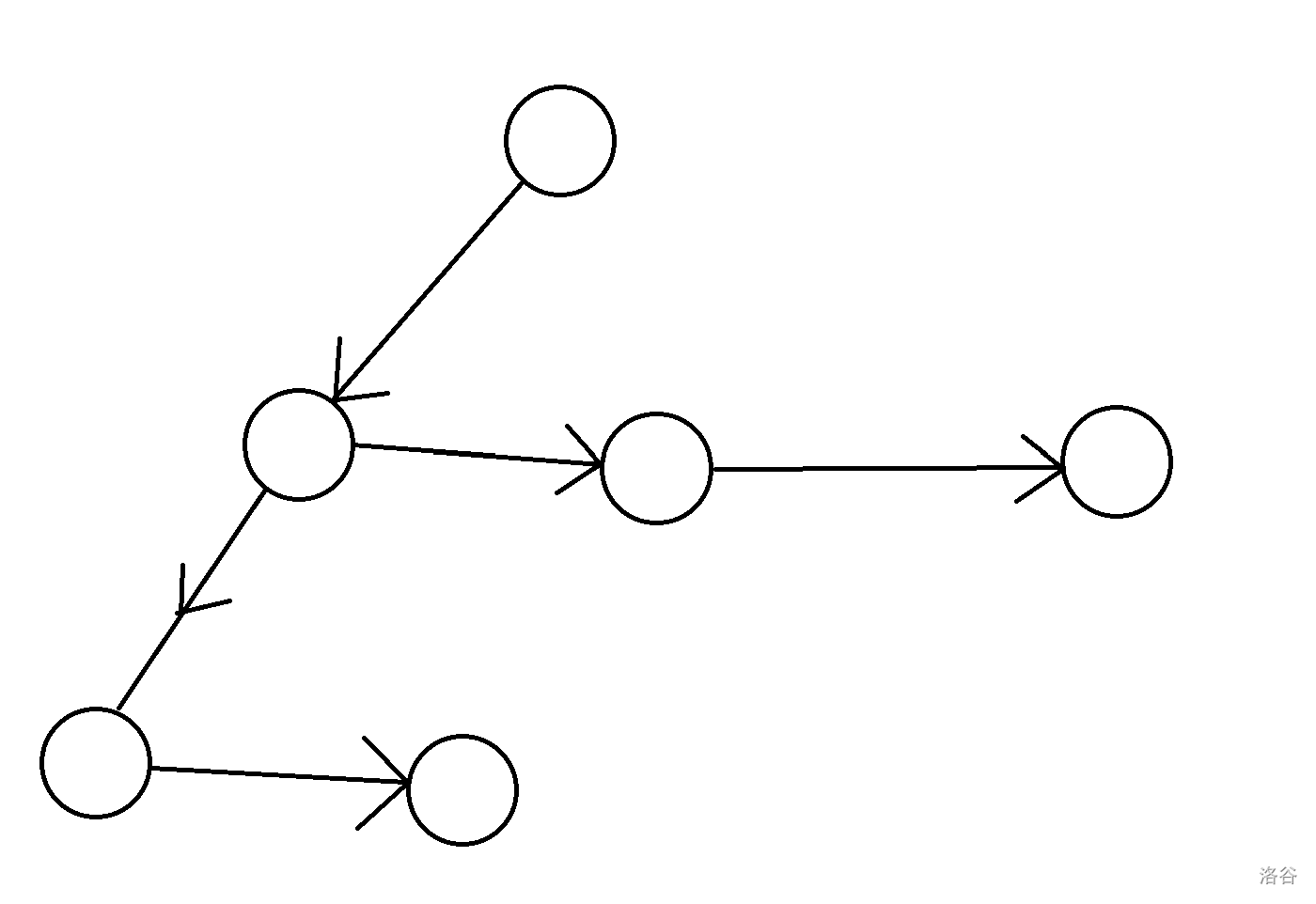
但是这样还不够。我们注意到,如果一个儿子 \(u\) 他的最大儿子为 \(x\),满足对于他的下一个兄弟的编号 \(v\),\(x<v\),那么我们就可以把 \(v\) 放到 \(u\) 下变成 \(x\) 的兄弟,所以我们还会有这样的边:
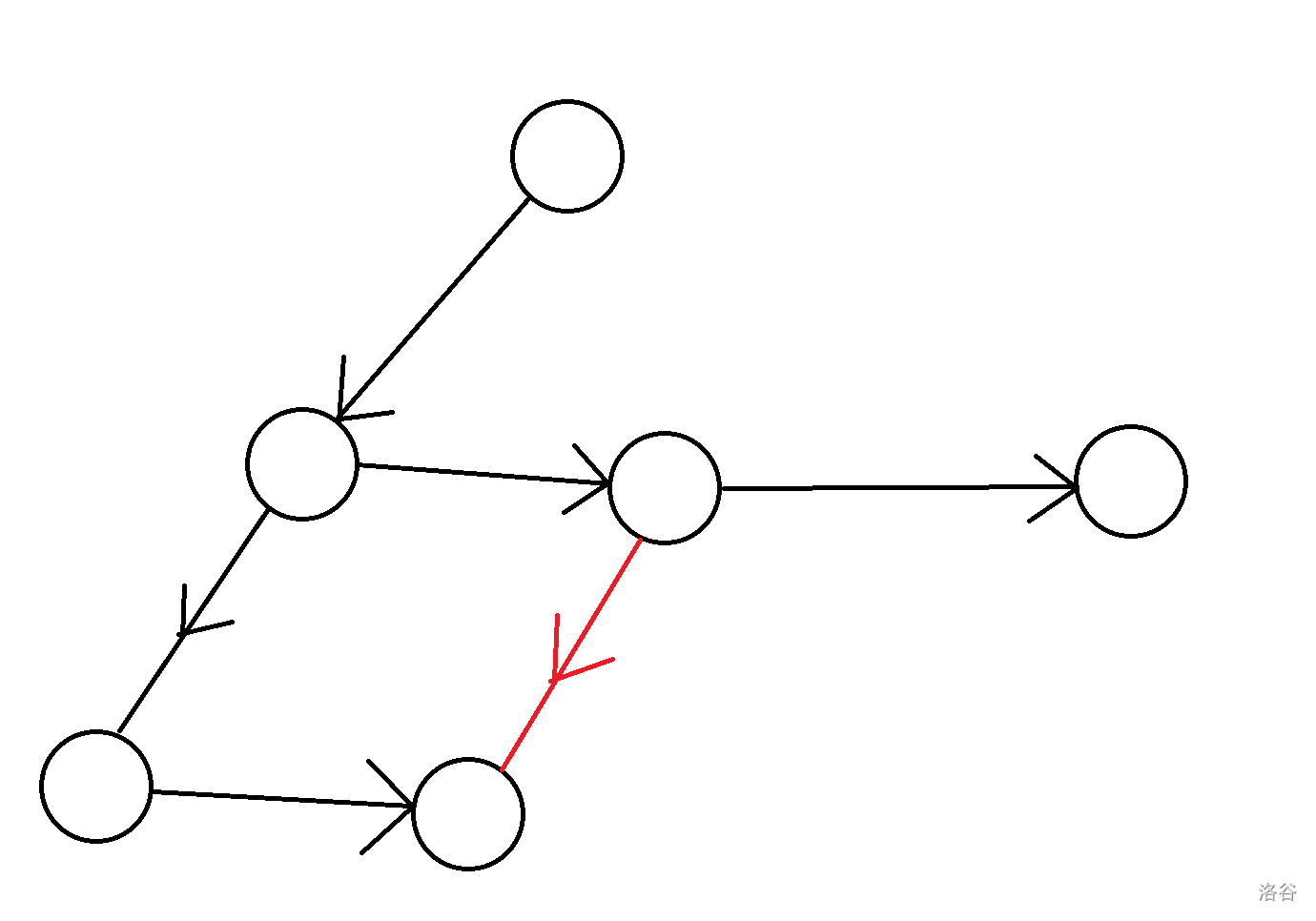
发现一个问题,原本我们的有向边是一个外向树结构,加入这些红边之后就变成 dag 就完蛋了,所以我们考虑容斥,容斥成没有限制减去逆向。注意到逆向了之后就可以把 \((u,v)\) 间的这条边给直接扔掉,还是一颗树。
因为外向树的拓扑序是 \(\frac{n!}{\prod sz_u}\),我们先把 \(n!\) 提出来。
考虑 dp 去算这个 \(\frac{1}{sz}\) 的乘积之和,首先肯定要有一个代表 \(u\) 的子树大小。注意到最后一个儿子并没有一条向上的边不太一样,所以我们还需要记录最后一个儿子的子树大小。
记 \(dp_{i,j}\) 代表我有一个 \(u\) 为根的 \(i\) 大的子树,同时还另外有一个 \(j\) 大的儿子要并到 \(u\) 的儿子里。因为 \(i\) 还有可能在父亲的位置并上来一个子树,所以我们先不考虑 \(i\) 这里 \(\frac{1}{i}\) 的贡献。
考虑枚举子树中第一个儿子,讨论:
-
如果只有一个儿子,那么 \(dp_{i,j}\leftarrow \frac{1}{i+j-1}dp_{i-1,0}\)。因为我考虑 \(u\rightarrow v\) 这里分别是 \(i-1,j\) 的大小,再加上一个根,所以状态是这样,同时有 \(\frac{1}{i+j-1}\)系数。
-
否则考虑枚举这个儿子的大小为 \(k\),那么 \(dp_{i,j}\leftarrow \frac{1}{i+j-1}\sum\limits_{k=2}^{i-2}dp_{i-k,j}\times (dp_{k, 0}-dp_{k,i-1-k+j})\),首先 \(dp_{i-k,j}\) 就是我后面的儿子的贡献,然后这个做差就是考虑容斥,第一个是不并,第二个是并上来 \(u\) 后面的兄弟和 \(j\),所以是 \(i-1-k+j\) 的大小。
最后记得答案是 \(\frac{1}n dp_{n,0}n!\)。
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 805;
int n, mod, dp[maxn][maxn], inv[maxn];
void prepare() {inv[0] = inv[1] = 1;for (int i = 2; i <= n; i++)inv[i] = (mod - mod / i) * inv[mod % i] % mod;
}
signed main() {cin >> n >> mod;dp[1][0] = 1;prepare();for (int i = 2; i <= n; i++) {for (int j = 0; j <= n - i; j++) {int res = dp[i - 1][0];for (int k = 2; k <= i - 2; k++)res = (res + (dp[k][0] - dp[k][i - 1 - k + j] + mod) % mod * dp[i - k][j] % mod) % mod;dp[i][j] = res * inv[i + j - 1] % mod;}}dp[n][0] = dp[n][0] * inv[n] % mod;for (int i = 1; i <= n; i++)dp[n][0] = dp[n][0] * i % mod;cout << dp[n][0] << endl;return 0;
}



















