三元组 - MKT

三元组

[62] B. Jiang, Y. Zhu, and M. Liu, “A triangle feature based map-tomap matching and loop closure for 2d graph slam,” in Proc. of the International Conference on Robotics and Biomimetics (ROBIO). IEEE, 2019, pp. 2719–2725.

[63] C. Yuan, J. Lin, Z. Zou, X. Hong, and F. Zhang, “STD: Stable triangle descriptor for 3D place recognition,” in Proc. of the IEEE Intl. Conf. on Robot. and Autom. (ICRA). IEEE, 2023, pp. 1897–1903.

[64] Z. Zou, C. Yuan, W. Xu, H. Li, S. Zhou, K. Xue, and F. Zhang, “LTAOM: Long-term association lidar–imu odometry and mapping,” J. Field Robot. (JFR), 2024.

[65] C. Yuan, J. Lin, Z. Liu, H. Wei, X. Hong, and F. Zhang, “BTC: A binary and triangle combined descriptor for 3d place recognition,” IEEE Trans. Robot. (TRO), 2024.

在这三篇论文中，三元组是如何描述一个物体的拓扑信息？基本原理和讲解

好的，这是一个非常专业且深入的问题。这三篇论文（[62], [63], 和 [65]）都使用了“三角形”或“三元组”作为核心描述符，但它们的具体应用场景、技术细节和侧重点有所不同。下面我将为您详细讲解这三篇论文中，三元组（Triplet）如何描述物体的拓扑信息，包括其基本原理和核心思想。

核心思想：为什么使用三元组？

在机器人感知（尤其是SLAM和地点识别）中，一个根本性挑战是如何对环境进行稳定、独特且对视角变化鲁棒的描述。

传统的特征点（如SIFT, ORB）在3D点云或大规模环境中可能不够稳定或区分度不足。

三元组（或三角形）描述符的基本原理在于，它不依赖于单个点的绝对坐标，而是描述点与点之间的相对几何关系。这种关系构成了局部区域的拓扑和几何不变性。

拓扑不变性：拓扑关注的是连接关系，而非精确距离或角度。一个由三个关键点构成的三角形，其存在性（即这三个点是否构成一个稳定的结构）本身就是一个拓扑信息。无论从哪个视角看，只要这三个点能被同时观测到，它们构成的“关系”就是存在的。
几何鲁棒性：三角形的几何属性（如边长比例、角度）对噪声、点云密度变化和轻微的视角变化相对不敏感。与单点坐标相比，这些相对测量值稳定得多。

简单来说，将一个物体或场景的局部结构抽象成一系列相互连接的三元组，就是在用一种“关系网络”来描述它。这个网络抓住了结构的本质，过滤掉了绝对坐标带来的不稳定性。

三篇论文的分别讲解

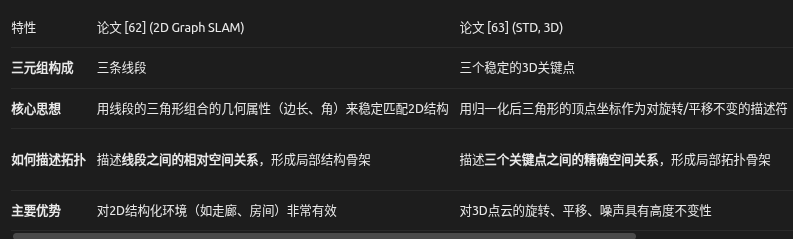
1. 论文 [62]: 基于三角形特征的 2D 图SLAM 回环检测

应用场景：2D 激光SLAM，主要用于地图与地图之间的匹配和回环检测。
三元组是什么：这里的“三元组”不是三个点，而是三个线段（或称为“线特征”）。论文从2D激光点云中提取出线段特征，然后选择三个线段构成一个三角形。
如何描述拓扑信息：
1. 特征提取：从一帧激光数据中提取出多条线段。
2. 三角形构造：从这些线段中选出三条，构成一个三角形。这个三角形的三个顶点是三条线段的交点或延长线的交点。
3. 描述符生成：用这个三角形的几何属性作为描述符，主要包括：
  - 边长：三角形的三条边的长度。
  - 角度：三角形的三个内角。
4. 拓扑匹配：当构建新地图时，系统会生成许多这样的“三角形描述符”。在进行回环检测时，它会将当前帧的三角形描述符与已有地图中的描述符进行匹配。如果找到足够多的、几何属性相似的三角形，就认为找到了一个回环。
核心贡献：将环境的结构从“一堆散乱的线段”提升为“由线段构成的稳定三角形结构”。
三角形的几何属性（边长、角度）比单一线段的方向、长度要稳定得多，因为它编码了三条线段之间的相对空间关系，这本身就是一种局部拓扑。

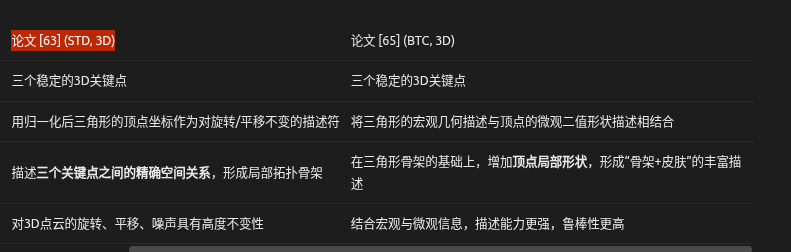
2. 论文 [63]: STD - 用于3D地点识别的稳定三角形描述符

应用场景：3D 激光点云中的地点识别，即判断当前扫描的场景是否是之前去过的地方。
三元组是什么：这里是严格意义上的三个点。论文首先从3D点云中提取一种稳定的关键点（称为“语义稳定点”），然后由三个关键点构成一个三角形。
如何描述拓扑信息：
1. 关键点提取：不是用传统的几何特征点（容易受噪声影响），而是寻找在多次扫描中都能稳定出现的点，通常与场景中的平面结构（如墙面、地面）的边界或交点相关。这保证了三角形的顶点是稳定存在的。
2. 三角形构造：在关键点的一个局部区域内，选择三个点构成一个三角形。为了增强独特性，这个三角形通常不是任意的，而是倾向于选择接近等边的三角形。
3. 描述符生成：STD描述符非常精巧，它分为两部分：
  - 几何向量（描述拓扑骨架）：这是一个3x3的矩阵。三角形的三条边构成了三个向量。
  - 对这个三角形进行一个特殊的归一化（将第一个点放在原点，第一条边与X轴对齐，整个三角形位于XY平面），然后计算这三个顶点在归一化坐标系下的坐标。
  - 这9个数字（3个点 x 3个坐标）就构成了描述三角形骨架的向量。这个过程本质上固定了三角形的“姿势”，使得描述符对旋转和平移不变。
  - 外观向量（描述表面信息）：在三角形的三个顶点附近，统计点云的法向量分布（通常用点云的主方向）。这为纯几何骨架增加了表面的纹理信息。
  - 将几何向量和外观向量拼接，形成最终的STD描述符。
核心贡献：STD的核心在于通过三角形的归一化坐标来编码三个点之间的精确空间关系。这种关系是内在的、不随机器人位姿变化的，因此非常适合地点识别。一个场景可以由许多这样的STD描述符构成一个“星座”，其独特的空间分布模式使得场景可以被唯一识别。

3. 论文 [65]: BTC - 用于3D地点识别的二值与三角形结合描述符

应用场景：同样是3D地点识别，可以看作是STD的改进和扩展。
三元组是什么：同样是三个关键点构成的三角形。
如何描述拓扑信息：
1. 结合两种描述符：BTC的创新点在于它不是只用三角形，而是将二值描述符（Binary Descriptor）和三角形描述符（Triangle Descriptor）结合起来。
2. 三角形描述符部分：这部分与STD思想一脉相承，也是利用三个关键点构成三角形，并通过归一化得到对旋转和平移不变的几何描述。它负责提供宏观的、结构性的拓扑信息。
3. 二值描述符部分：在三角形的每个顶点处，计算一个局部二值描述符（比如一种改进的BSC描述符）。这种描述符通过比较点邻域内不同维度的距离关系来生成一个二值串，它描述了顶点周围的微观局部形状特征。
4. 融合：将三角形的宏观几何描述符和三个顶点处的微观二值描述符组合在一起，形成一个更强大、信息更丰富的描述符。这样，BTC不仅描述了“这三个点之间的空间关系”（拓扑骨架），还描述了“这三个点各自长什么样”（局部纹理）。
核心贡献：BTC认为，单一的描述符可能在某些场景下失效。通过将基于三元组的全局拓扑描述与基于点的局部形状描述相结合，实现了优势互补，获得了比单一三角形描述符（如STD）更强的鲁棒性和区分度。

Generalizable and Efficient Scene Graph Registration【IEEE TRO】三元组是如何设计的？对比

好的，这是一个非常深刻的问题，直击了场景图注册领域的核心创新。IEEE TRO 上的论文《Generalizable and Efficient Scene Graph Registration》中提出的三元组设计，与之前我们讨论的基于“物理三角形”的方法有根本性的不同。它不再是描述一个由三个点构成的几何三角形，而是描述场景图中三个节点之间的抽象语义关系。这是一种从几何层到关系层的跃升。为了让对比更加清晰直观，我首先用一个表格来总结核心差异，然后再进行详细讲解。

本文“关系三元组”的设计原理详解

这篇论文的核心问题是场景图注册：给定两个在不同条件下生成的场景图（例如，一个来自CAD模型，一个来自真实世界的激光扫描），如何找到它们之间的正确对应关系。场景图中的节点是物体（如“椅子1”、“桌子1”），边是物体间的语义关系（如“椅子1” UNDER“桌子1”）。

1. 三元组的设计是什么？

这篇论文中的“三元组”定义为场景图中的一个三节点子图，包含一个中心主体节点（Subject）、一个关系谓词（Predicate）和一个周边客体节点（Object）。它描述的是两个物体通过一个关系连接起来的基本单元。

示例：(Chair1, ON, Floor) 和 (Monitor1, ON, Desk1) 就是两个不同的三元组。

2. 如何用三元组进行描述和匹配？

论文的关键创新在于如何量化一个三元组的“描述能力”，并利用它进行高效匹配。

其基本流程如下：

a) 三元组编码（描述符生成）

对于一个三元组 (S, P, O)，论文不是直接使用物体的标签（如“椅子”），因为不同场景图中同类物体的实例ID是未知的。取而代之，论文为每个节点和每条边提取一个特征向量：

节点特征：编码物体本身的属性，例如：
- 语义类别的嵌入向量（如“椅子”这个词的Word2Vec向量）。
- 几何属性：物体的尺寸、体积、点云特征等。
边特征：编码关系的属性，例如关系的类型（ON, IN等）的嵌入向量。

然后，通过一个神经网络（如图神经网络或MLP）将中心节点 S的特征、关系 P的特征和周边节点 O的特征融合起来，生成一个代表这个三元组的固定长度的描述符向量。

b) 重要性评分（泛化性的关键）论文的核心观点是：并非所有三元组都同样重要。一个独特的三元组比一个普遍的三元组能提供更强的匹配信号。

普遍的三元组：(Chair, IN, Room) 在一个办公室场景中非常普遍，很多椅子都满足这个关系，因此它的区分度很低。
独特的三元组：(Monitor, ON, Desk) 且 (Desk, FACE_TO, Window) 的组合就非常独特，能清晰地定位一个特定的办公桌。

因此，论文会为每个三元组计算一个重要性分数。这个分数可以基于该三元组在场景图中出现的稀有性，或者通过机器学习模型学习得到。重要性高的三元组在匹配过程中拥有更大的权重。

c) 基于三元组的场景图匹配（注册）

注册过程不再是逐个匹配点或特征，而是匹配这些关系三元组：

三元组提取：从源场景图和目标场景图中分别提取所有可能的三元组。
描述符计算与评分：为每个三元组计算描述符和重要性分数。
相似度计算：计算源场景图中一个三元组与目标场景图中所有三元组的描述符之间的相似度（如余弦相似度）。
投票与对齐：如果两个三元组非常相似，它们就构成了一个“三元组对应”。这个对应关系会为它们所包含的节点对应关系（如源图的 Chair1对应目标图的 ChairA）进行“投票”。
全局优化：最终，通过收集所有的三元组对应投票，问题可以转化为一个图匹配优化问题，目标是找到一个节点对应关系，使得所有重要三元组的相似度得分之和最大。这个过程是高效的，因为它避免了对整个图进行暴力匹配。

与STD/BTC等几何三元组的本质对比

抽象层次不同：
- 几何三元组 (STD/BTC)：工作在几何空间。描述的是“点A、点B、点C在物理空间中构成一个三角形，其边长和角度是多少”。它是低层的、数据驱动的。
- 关系三元组 (本文)：工作在语义关系空间。描述的是“物体A（椅子）和物体B（桌子）之间存在‘UNDER’关系”。它是高层的、知识驱动的。
泛化能力来源不同：
- 几何三元组：泛化性来自几何不变性。同一把椅子，从不同角度看，提取的STD描述符应该相似。
- 关系三元组：泛化性来自语义不变性。即使两把椅子型号不同、点云密度差异巨大，但只要它们都“在”一张“桌子”下面，这个 (Chair, UNDER, Desk)的关系模式就是一致的。这使得它能处理点云质量差、部分遮挡、甚至跨模态（CAD模型 vs. 真实扫描）的挑战性场景。
效率提升原因不同：
- 几何三元组：效率通过描述符的简洁性（一个固定维度的向量）和快速最近邻搜索实现。
- 关系三元组：效率通过重要性采样实现。系统只关注那些最具区分度的关系模式，避免了在大量普通且无信息的物体关系上进行无效计算。