哑演算基础理论

前言：

这篇文章基本是关于 Steven Roman, The Umbral Calculus 1~3 章的中文翻译（其实可能不太算翻译了，改的原文结构还是挺多的），原文可从 Z-Library 下载 . 有问题请在评论区反馈！

---

\[\newcommand{\lmid}{\mathrel{\bigg\vert}}\newcommand{\bmid}{\mathrel{\Big\vert}}\newcommand{\Lmid}{\mathrel{\Bigg\vert}}\newcommand{\ord}{\operatorname{ord}}\newcommand{\I}{{\langle-1\rangle}} \]

目录

• 0. 基本定义
  • 1. 代数
  • 2. 形式幂级数的序
  • 3. Sheffer 类函数
• 1. Sheffer 序列
  • 1. 本影代数
  • 2. 线性算子
  • 3. Sheffer 序列
  • 4. 相关序列
  • 5. Appell 序列
  • 6. 一些例子
• 2. 算子及其伴随
  • 1. \(\mathbb P^*\) 上的连续算子
  • 2. \(\mathbb P^*\) 上的自同构和导子
  • 3. 伴随
  • 4. 本影算子和本影复合
  • 5. Sheffer 算子和本影复合
  • 6. 本影移位和相关序列的递推式
  • 7. Sheffer 移位和 Sheffer 序列的递推式
  • 8. 转换公式

0. 基本定义

1. 代数

域 \(F\) 上的（结合）代数是附加乘法的向量空间 \(A\)：对于域 \(F\) 上的向量空间 \(A\)，取乘法 \(\times\) 使得 \((A,+,\times)\) 是环，且 \(\times\) 关于数乘结合：

\[\forall a\in F,\,u,v\in A\text{ s.t. }a(u\times v)=(au)\times v=u\times(av) \]

2. 形式幂级数的序

对于形式幂级数 \(\displaystyle f(x)=\sum_{i\ge 0}a_ix^i\)，定义它的序 \(\ord(f)\) 是最小的 \(n\) 使得 \(a_n\neq0\) . 特别的，\(\ord(0)=\infty\) .

若形式幂级数 \(f\) 满足 \(\ord(f)=0\)，则称 \(f\) 是可逆级数 . 若形式幂级数 \(f\) 满足 \(\ord(f)=1\)，则称 \(f\) 是 delta 级数 .

3. Sheffer 类函数

多项式序列的一个重要种类：Sheffer 序列（或在稍有差别的形式上，Sheffer A-type zero / poweroids 组成的序列）. 关于 Sheffer 序列有很多种定义，我们只在此指出一点：\(s_n(x)\) 是 Sheffer 序列当且仅当其生成函数有形式：

\[\sum_{k\ge0}\dfrac{s_k(x)}{k!}t^k=A(t)\mathrm e^{xB(t)} \]

其中 \(A(t)\) 是可逆级数，\(B(t)\) 是 delta 级数（我们在 1.3 节会重申这一点）.

Sheffer 序列包含很多重要的多项式序列，例如 Hermite 多项式、Laguerre 多项式、Bernoulli 多项式、Abel 多项式、中心阶乘多项式 (central factorial polynomial) 等 .

1. Sheffer 序列

1. 本影代数

令 \(\mathbb P\) 是 \(\mathbb C\) 上关于 \(x\) 的多项式的代数，\(\mathbb P^*\) 是 \(\mathbb P\) 上线性泛函的对偶向量空间，记 \(\langle L\mid p(x)\rangle\) 是线性泛函 \(L\) 作用在多项式 \(p(x)\) 上的结果 .

我们特此声明并确认，线性性：

\[\begin{aligned}&\langle L+M\mid p(x)\rangle=\langle L\mid p(x)\rangle+\langle M\mid p(x)\rangle\\&\langle cL\mid p(x)\rangle=c\langle L\mid p(x)\rangle\end{aligned} \]

那么 \(L\) 由每个 \(\langle L\mid x^n\rangle\) 唯一确定 . 考虑 \(\mathcal F=\mathbb C[[t]]\)（即 \(\mathbb C\) 上关于 \(t\) 的形式幂级数）上的元素：

\[f(t)=\sum_{k\ge 0}a_k\dfrac{t^k}{k!} \]

定义 \(\langle f(t)\mid x^n\rangle=a_n\) 以将线性泛函与形式幂级数建立起联系：

\[f_L(t)=\sum_{k\ge 0}\langle L\mid x^k\rangle\frac{t^k}{k!} \]

容易验证 \(L\) 和 \(f_L(t)\) 在 \(\langle\cdots\mid p(x)\rangle\) 上的表现一致 .

称这样将形式幂级数与线性泛函作关联的代数结构 \(\mathcal F\) 是本影代数 (umbral algebra) .

对于 \(f(t)\in\mathcal F\)，若 \(f\) 是 delta 级数，则 \(f\) 对应的线性泛函是 delta 泛函，类似可以定义可逆泛函 .

由形式幂级数的经验可以显然得到一系列性质：

性质 1.1.1

\[\langle f(t)g(t)\mid x^n\rangle=\sum_{k=0}^n\dbinom nk\langle f(t)\mid x^k\rangle\langle g(t)\mid x^{n-k}\rangle \]

\[\langle f(t)\mid xp(x)\rangle=\langle\partial_tf(t)\mid p(x)\rangle \]

\[\langle f(at)\mid p(x)\rangle=\langle f(t)\mid p(ax)\rangle \]

性质 1.1.2

对每个 \(k\ge 0\) 有 \(\ord(f_k(t))=k\)，且 \(\langle f_k(t)\mid p(x)\rangle=\langle f_k(t)\mid q(x)\rangle\)，则 \(p(x)=q(x)\) .

对每个 \(k\ge 0\) 有 \(\deg(p_k(t))=k\)，且 \(\langle f(t)\mid p_k(x)\rangle=\langle g(t)\mid p_k(x)\rangle\)，则 \(f(t)=g(t)\) .

一些例子：

• 赋值泛函 \(\mathrm e^{yt}\)：
  \[\langle\mathrm e^{yt}\mid p(x)\rangle=p(y) \]

• 前向差分泛函 \(\mathrm e^{yt}-1\)：
  \[\langle\mathrm e^{yt}-1\mid p(x)\rangle=p(y)-p(0) \]

• Abel 泛函 \(t\mathrm e^{yt}\)：
  \[\langle t\mathrm e^{yt}\mid p(x)\rangle=p'(y) \]

• 几个积分相关的泛函：
  \[\begin{aligned}\left\langle \frac{1}{1-t}\lmid p(x)\right\rangle&=\int_0^{\infty} p(u)\mathrm e^{-u}\mathrm d u\\\left\langle \frac{\mathrm e^{yt}-1}{t}\lmid p(x)\right\rangle&=\int_0^y p(u)\mathrm d u\end{aligned} \]

• 小应用：
  \[\left\langle \frac{1+\mathrm e^{yt}}{2} \lmid p(x)\right\rangle=\frac{p(0)+p(y)}2 \]

2. 线性算子

定义 \(t^k=\dfrac{\partial^k}{\partial x^k}\) 是 \(k\) 阶微分算子，则：

\[t^kx^n=n^{\underline k}x^{n-k} \]

（注：易知此处 \(k>n\) 时 \(t^kx^n=0\)）

那么对于关于 \(t\) 的形式幂级数 \(f\)，可以写出它所能产生的效果：

\[f(t)=\sum_{k\ge 0}a_k\dfrac{t^k}{k!}\qquad f(t)x^n=\sum_{k=0}^n\dbinom nka_kx^{n-k} \]

这里使用 \(f(t)\) 和 \(p(x)\) 的并置 \(f(t)p(x)\) 来标识算子到函数的作用 . 注意区分 \(\langle f(t)\mid p(x)\rangle\) 和 \(f(t)p(x)\) 两种记号的区别 .

Remark

一般地，可以取这样的线性算子 \(t\)：

\[f(t)x^n=\sum_{k=0}^n\dfrac{c_n}{c_{n-k}}a_kx^{n-k} \]

其中 \(f\in\mathcal F\)，\(c\) 是一个序列 . 可以通过选定 \(c\) 的取值来得到各种种类的 \(t\)，并且其性质基本类似 .

对于 \(f(t)\in\mathcal F\)，若 \(f\) 是 delta 级数，则 \(f\) 对应的线性算子是 delta 算子，类似可以定义可逆算子 .

基本运算定律：

性质 1.2.1

\[(f(t)g(t))p(x)=f(t)(g(t)p(x)) \]

\[f(t)g(t)p(x)=g(t)f(t)p(x) \]

对于 \(\ord(f_k(t))=k\)，

\[\left(\sum_{k\ge0}a_kf_k(t)\right)p(x)=\sum_{k\ge0}a_k(f_k(t)p(x)) \]

关键性质：

定理 1.2.1

\[\langle f(t)g(t)\mid p(x)\rangle=\langle g(t)\mid f(t)p(x)\rangle \]

可以通过定义证明：

\[\begin{aligned}\langle g(t)\mid f(t)x^n\rangle&=\left\langle g(t)\Lmid\sum_{k=0}^n\dbinom nk\langle f(t))\mid x^k\rangle x^{n-k}\right\rangle\\&=\sum_{k=0}^n\dbinom nk\langle f(t)\mid x^k\rangle\langle g(t)\mid x^{n-k}\rangle\\&=\langle f(t)g(t)\mid p(x)\rangle\end{aligned} \]

推论：\(\langle f(t)\mid p(x)\rangle=\langle t^0\mid f(t)p(x)\rangle\)，即向 \(p(x)\) 施加泛函 \(f(t)\) 等价于向 \(p(x)\) 施加算子 \(f(t)\) 并代入 \(x=0\) .

关于之前线性泛函的例子，对应到线性算子的效果：

• 翻译算子 \(\mathrm e^{yt}\)：
  \[\mathrm e^{yt}p(x)=p(x+y) \]

• 前向差分算子 \(\mathrm e^{yt}-1\)：
  \[(\mathrm e^{yt}-1)p(x)=p(x+y)-p(x) \]

• Abel 算子 \(t\mathrm e^{yt}\)：
  \[t\mathrm e^{yt}p(x)=p'(x+y) \]

• 几个积分相关的算子：
  \[\begin{aligned}\frac{1}{1-t}p(x)&=\int_0^{\infty}p(x+u)\mathrm e^{-u}\mathrm d u\\\frac{\mathrm e^{yt}-1}{t}p(x)&=\int_x^{x+y}p(u)\mathrm d u\end{aligned} \]

• 小应用：
  \[\frac{1+\mathrm e^{yt}}{2}p(x)=\frac{p(x)+p(x+y)}2 \]

注意，同线性泛函的情况不同，并不是每一个线性算子都对应一个形式幂级数 . 例如算子 \(p(x)\to xp(x)\) 就不对应任何形式幂级数 \(f(t)\) . 称一个 \(\mathbb P\) 上的线性算子 \(T\) 有形式 \(g(t)\) 当且仅当对于每个 \(p(x)\) 有 \(Tp(x)=g(t)p(x)\) . 下面讨论怎样的线性算子具有形式幂级数形式 .

引理 1.2.1

\(f(t)\) 是 delta 算子，\(T\) 是和 \(f(t)\) 交换的线性算子（即 \(f(t)(Tp(x))=T(f(t)p(x))\)）. 则对于每个多项式 \(p(x)\)，有 \(\deg Tp(x)\le\deg p(x)\) .

如果条件不成立，则存在整数 \(m\ge0\) 使得 \(\deg Tx^m\ge m+1\) . 因为 \(\ord(f(t))=1\)，所以 \(\deg f(t)p(x)=\deg p(x)-1\) . 只要 \(\deg p(x)>0\)，就有

\[0=Tf(t)^{m+1}x^m=f(t)^{m+1}Tx^m\neq 0 \]

矛盾！故命题得证 .

定理 1.2.2

一个 \(\mathbb P\) 上的线性算子 \(T\) 有形式 \(g(t)\) 当且仅当它和微分算子 \(t\) 交换 .

充分性：若 \(T\) 有形式 \(g(t)\)，那么 \(T\) 和 \(\mathcal F\) 上的每个算子都交换 .

必要性：令 \(\displaystyle g(t)=\sum_{k\ge0}\dfrac{\langle t^0\mid Tx^k\rangle}{k!}t^k\)，则：

\[g(t)x^n=\sum_{k=0}^n\dbinom nk\langle t^0\mid Tx^k\rangle x^{n-k} \]

由定理 1.2.1，我们知道：

\[\langle t^0\mid Tx^k\rangle=\dfrac{k!}{n!}\langle t^0\mid Tt^{n-k}x^n\rangle=\dfrac{k!}{n!}\langle t^0\mid t^{n-k}Tx^n\rangle=\dfrac{k!}{n!}\langle t^{n-k}\mid Tx^n\rangle \]

所以

\[\begin{aligned}g(t)x^n&=\sum_{k=0}^n\langle t^{n-k}\mid Tx^n\rangle\dfrac{x^{n-k}}{k!}\\&=\sum_{k=0}^n\langle t^k\mid Tx^n\rangle\dfrac{x^k}{k!}\\&=Tx^n\end{aligned} \]

从而 \(T\) 有形式 \(g(t)\) .

推论 1.2.2 (1)

一个 \(\mathbb P\) 上的线性算子 \(T\) 有形式 \(g(t)\) 当且仅当它和任意一个 delta 算子交换 .

充分性显然，必要性：令 \(T\) 和 delta 算子 \(f(t)\) 交换，则存在常数列 \(a_k\) 使得

\[t=\sum_{k\ge0}a_kf(t)^k \]

则：

\[\begin{aligned}Ttx^n&=T\sum_{k=0}^na_kf(t)^kx^n\\&=\sum_{k=0}^na_kf(t)^kTx^n\\&=tTx^n\end{aligned} \]

从而 \(T\) 和 \(t\) 交换，调用定理 1.2.2 即可 .

推论 1.2.2 (2)

一个 \(\mathbb P\) 上的线性算子 \(T\) 有形式 \(g(t)\) 当且仅当它和任意一个翻译算子 \(\mathrm e^{yt}\) 交换 .

显然！

3. Sheffer 序列

后记 \(s_n(x)\) 是度数为 \(n\) 的多项式 .

定理 1.3.1

\(f(t)\) 是 delta 级数，\(g(t)\) 是可逆级数，则存在一个唯一的多项式序列 \(s_n(x)\) 满足正交条件

\[\langle g(t)f(t)^k\mid s_n(x)\rangle=n![n=k]\qquad\forall n,k\ge 0 \]

唯一性由定理 1.2.1 指出 . 对于存在性，令：

\[s_n(x)=\sum_{j=0}^na_{n,j}x^j\qquad g(t)f(t)^k=\sum_{i\ge k}b_{k,i}t^i \]

其中 \(b_{k,k}\neq 0\) . 那么可以将正交条件转写为：

\[\begin{aligned}n![n=k]&=\left\langle\sum_{i\ge k}b_{k,i}t^i\Lmid\sum_{j=0}^na_{n,j}x^j\right\rangle\\&=\sum_{i\ge k}\sum_{j=0}^nb_{k,i}a_{n,j}\langle t^i\mid x^j\rangle\\&=\sum_{i=k}^nb_{k,i}a_{n,i}i!\end{aligned} \]

上三角矩阵，对角线上的元素为 \(\frac1{b_{i,i}}\)，必然有解 .

对于定理 1.3.1 这样的序列 \(s_n(x)\)，称 \((g(t),f(t))\) 是 Sheffer 序列，\(s_n(x)\) Sheffer 于 \((g(t),f(t))\)（“对于 ... Sheffer”）. 注意此处 \(f(t)\) 是 delta 级数，\(g(t)\) 是可逆级数 .

值得注意的两类 Sheffer 序列：

• 称 \((1,f(t))\) 是 \(f(t)\) 的相关 (associated) 序列，\(s_n(x)\) 相关于 \(f(t)\) .
• 称 \((g(t),t)\) 是 \(g(t)\) 的 Appell 序列，\(s_n(x)\) Appell 于 \(g(t)\) .

注：在某些其它资料中，\(s_n(x)\) Appell 当且仅当在此处的定义中 \(n!s_n(x)\) Appell .

因为 \(\langle t^k\mid x^n\rangle=n![n=k]\)，所以 \(p_n(x)=x^n\) 相关于 \(f(t)=t\) .

下面展示本影演算 (umbral calculus) 中最实用的两个结果 . 第一个表明如何表示几何级数 \(g(t)f(t)^k\) 中的项：

定理 1.3.2 (展开定理, The Expansion Theorem)

令 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则对于任意 \(h(t)\in\mathcal F\)，

\[h(t)=\sum_{k\ge0}\dfrac{\langle h(t)\mid s_k(x)\rangle}{k!}g(t)f(t)^k \]

注意到：

\[\left\langle\sum_{k\ge0}\dfrac{\langle h(t)\mid s_k(x)\rangle}{k!}g(t)f(t)^k\Lmid s_n(x)\right\rangle=\sum_{k\ge0}\dfrac{\langle h(t)\mid s_k(x)\rangle}{k!}\langle g(t)f(t)^k\mid s_n(x)\rangle=\langle h(t)\mid s_n(x)\rangle \]

然后调用性质 1.1.2 即可完成证明 .

展开定理的多项式模拟展示了如何将任意多项式表为若干 Sheffer 序列中的多项式的线性组合：

定理 1.3.3 (多项式展开定理, The Polynomial Expansion Theorem)

令 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则对于任意多项式 \(p(x)\)，

\[h(t)=\sum_{k\ge0}\dfrac{\langle g(t)f(t)^k\mid p(x)\rangle}{k!}s_k(x) \]

证明：与定理 1.3.2 类似 .

现在将要探讨如何描述 Sheffer 序列 . 从生成函数开始：

定理 1.3.4

序列 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\) 当且仅当

\[\dfrac1{g(f^\I(t))}\mathrm e^{yf^\I(t)}=\sum_{k\ge0}\dfrac{s_k(y)}{k!}t^k \]

对于每个 \(y\in\mathbb C\) 成立 .

证明：

充分性：若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则由展开定理知：

\[\begin{aligned}&\mathrm e^{yt}=\sum_{k\ge0}\dfrac{\langle\mathrm e^{yt}\mid s_k(x)\rangle}{k!}g(t)f(t)^k=\sum_{k\ge0}\dfrac{s_k(y)}{k!}g(t)f(t)^k\\\iff&\dfrac1{g(t)}\mathrm e^{yt}=\sum_{k\ge0}\dfrac{s_k(y)}{k!}f(t)^k\\\iff&\dfrac1{g(f^\I(t))}\mathrm e^{yf^\I(t)}=\sum_{k\ge0}\dfrac{s_k(y)}{k!}t^k\end{aligned} \]

必要性：若 \(r_n(x)\) Sheffer 于 \((g(t),f(t))\)，则：

\[\sum_{k\ge0}\dfrac{r_k(y)}{k!}t^k=\dfrac1{g^\I(f(t))}\mathrm e^{yf^\I(t)}=\sum_{k\ge0}\dfrac{s_k(y)}{k!}t^k \]

从而 \(r_k(x)=s_k(x)\) .

若我们考虑关于 \(x,t\) 的双变量生成函数，则可以将定理 1.3.4 的条件重写为：

\[\dfrac1{g(f^\I(t))}\mathrm e^{xf^\I(t)}=\sum_{k\ge0}\dfrac{s_k(x)}{k!}t^k \]

虽然这是生成函数的常见形式，但是这里有一个小问题：当我们将 \(x,t\) 视为形式变元时，\(x,t\) 是可交换的 . 但是将 \(t\) 看做线性算子时，\(x,t\) 并不是可交换的 . 所以当我们使用它时，只将 \(t\) 视为形式变元，而不认为其值有意义 .

在查阅文献时，必须谨慎对待 Sheffer 序列，因为可能系数上差一个阶乘……（唉等你真查的时候就知道了）

生成函数导出了一个 Sheffer 序列的描述：

定理 1.3.5

序列 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\) 当且仅当

\[s_n(x)=\sum_{k=0}^n\left\langle g(f^\I(t))^{-1}f(t)^k\bmid x^n\right\rangle\dfrac{x^k}{k!} \]

这被称为 \(s_n(x)\) 的共轭表示 .

证明：在定理 1.3.4 中等式两侧同时施加 \(\langle\cdots\mid x^n\rangle\) 即可 .

定理 1.3.6

序列 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\) 当且仅当 \(g(t)s_n(x)\) 是 \(f(t)\) 的相关序列 .

证明：只需要注意到 \(\langle f(t)^k\mid g(t)s_n(x)\rangle=\langle g(t)f(t)^k\mid s_n(x)\rangle\)，则由定理 1.3.5 易得 .

定理 1.3.6 指出，每个相关序列都产生一系列 Sheffer 序列，每个序列对应一个可逆算子 \(g(t)\) .

定理 1.3.7

序列 \(s_n(x)\) 对于某个 \(g(t)\) Sheffer 于 \((g(t),f(t))\) 当且仅当

\[f(t)s_n(x)=ns_{n-1}(x) \]

对每个 \(n\ge0\) 成立 .

证明：

充分性：若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则

\[\begin{aligned}\langle g(t)f(t)^k\mid f(t)s_n(x)\rangle&=\langle g(t)f(t)^{k+1}\mid s_n(x)\rangle\\&=n![n=k+1]\\&=n(n-1)![n-1=k]\\&=\langle g(t)f(t)^k\mid ns_{n-1}(x)\rangle\end{aligned} \]

从而 \(f(t)s_n(x)=ns_{n-1}(x)\) .

必要性：令 \(p_n(x)\) 是 \(f(t)\) 的相关序列，定义线性算子 \(T\)：\(Ts_n(x)=p_n(x)\) . 由于 \(s_n(x),p_n(x)\) 是 \(\mathbb P\) 的一组基，所以 \(T\) 必然良定义且可逆 .

由充分性可得 \(f(t)p_n(x)=np_{n-1}(x)\)，从而：

\[Tf(t)s_n(x)=nTs_{n-1}(x)=np_{n-1}(x)=f(t)p_n(x)=f(t)Ts_n(x) \]

由推论 1.2.2 (2) 可知存在可逆级数 \(g(t)\) 使得 \(g(t)s_n(x)=p_n(x)\)，调用定理 1.3.6 即可完成证明 .

定理 1.3.8

令 \(s_n(x)\) Sheffer 于 \(((g(t),f(t)))\)，\(p_n(x)\) 相关于 \(f(t)\) . 则对于任意 \(h(t)\in\mathcal F\)，

\[h(t)s_n(x)=\sum_{k=0}^n\dbinom nk\langle h(t)\mid s_k(x)\rangle p_{n-k}(x) \]

证明：由展开定理：

\[h(t)=\sum_{k\ge 0}\dfrac{\langle h(t)\mid s_k(x)\rangle}{k!}g(t)f(t)^k \]

两边同时施加到 \(s_n(x)\) 上：

\[\begin{aligned}h(t)s_n(x)&=\sum_{k\ge0}\dfrac{\langle h(t)\mid s_k(x)\rangle}{k!}g(t)f(t)^ks_n(x)\\&=\sum_{k=0}^n\dbinom nk\langle h(t)\mid s_k(x)\rangle g(t)s_{n-k}(x)\\&=\sum_{k=0}^n\dbinom nk\langle h(t)\mid s_k(x)\rangle p_{n-k}(x)\end{aligned} \]

证明完毕 .

定理 1.3.9 (Sheffer 恒等式, The Sheffer Identity)

一个序列 \(s_n(x)\) 对于某个 \(g(t)\) Sheffer 于 \((g(t),f(t))\) 当且仅当

\[s_n(x+y)=\sum_{k=0}^n\dbinom nkp_k(y)s_{n-k}(x) \]

对于每个 \(y\in\mathbb C\) 成立 . 其中 \(p_n(x)\) 相关于 \(f(t)\) .

证明：

充分性：由展开定理：

\[\mathrm e^{yt}=\sum_{k\ge0}\dfrac{p_k(y)}{k!}f(t)^k \]

从而：

\[\begin{aligned}s_n(x+y)&=\mathrm e^{yt}s_n(x)\\&=\sum_{k\ge0}\dfrac{p_k(y)}{k!}f(t)^ks_n(x)\\&=\sum_{k\ge0}\dbinom nkp_k(y)s_{n-k}(x)\end{aligned} \]

必要性：考虑满足 Sheffer 恒等式的序列 \(s_n(x)\)，定义 \(T\) 上的线性算子：\(Ts_n(x)=p_n(x)\) .

由定理 1.3.6 可知只需证 \(T\) 有形式 \(g(t)\in\mathcal F\) . 由充分性知 \(p_n(x)\) 满足 Sheffer 恒等式，则

\[\begin{aligned}\mathrm e^{yt}Ts_n(x)&=\mathrm e^{yt}p_n(x)\\&=p_n(x+y)\\&=\sum_{k=0}^n\dbinom nkp_k(y)p_{n-k}(x)\\&=T\sum_{k=0}^n\dbinom nkp_k(y)s_{n-k}(x)\\&=Ts_n(x+y)\\&=T\mathrm e^{yt}s_n(x)\end{aligned} \]

从而 \(T\) 关于翻译算子 \(\mathrm e^{yt}\) 交换，接下来使用推论 1.2.2 (2) 即可完成证明 .

顺便一提，在此处交换 \(x,y\) 并令 \(y=0\) 立得

\[s_n(x)=\sum_{k=0}^n\dbinom nks_{n-k}(0)p_k(x) \]

这指出，给定一个 \(p_n(x)\) 相关于 \(f(t)\)，对于每个由 \(f(t)\) 作为 delta 泛函的 Sheffer 序列 \(s_n(x)\) 都由其常数项 \(s_n(0)\) 唯一确定 . 进一步的，对于任意满足 \(a_0\neq 0\) 的常数列 \(a\) 都可以由这种方式得到一个由 \(f(t)\) 作为 delta 泛函的 Sheffer 序列 .

具体地，考察

\[s_n(x)=\sum_{k=0}^n\dbinom nka_{n-k}p_k(x) \]

两侧同时施加 \(f(t)\)：

\[\begin{aligned}f(t)s_n(x)&=f(t)\sum_{k=0}^n\dbinom nka_{n-k}p_k(x)\\&=\sum_{i=1}^n\dbinom nkka_{n-k}p_{k-1}(x)\\&=n\sum_{k=1}^n\dbinom{n-1}{k-1}a_{n-1-(k-1)}p_{k-1}(x)\\&=n\sum_{k=0}^{n-1}\dbinom{n-1}ka_{n-1-k}p_k(x)\\&=ns_{n-1}(x)\end{aligned} \]

由定理 1.3.7 可知，\(s_n(x)\) 对于某个 \(g(t)\) Sheffer 于 \((g(t),f(t))\) .

Sheffer 序列的一个重要特征是它对于 \(\mathcal F\) 上乘法的表现（可以试比较下一个结果和性质 1.1.1）：

定理 1.3.10

令 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，\(p_n(x)\) 相关于 \(f(t)\) . 则对于任意 \(h(t),l(t)\in\mathcal F\)，

\[\langle h(t)l(t)\mid s_n(x)\rangle=\sum_{k=0}^n\dbinom nk\langle h(t)\mid s_k(x)\rangle\langle l(t)\mid p_{n-k}(x)\rangle \]

证明：由定理 1.3.8，

\[\begin{aligned}\langle h(t)l(t)\mid s_n(x)\rangle&=\langle l(t)\mid h(t)s_n(x)\rangle\\&=\left\langle l(t)\Lmid\sum_{k=0}^n\dbinom nk\langle h(t)\mid s_k(x)\rangle p_{n-k}(x)\right\rangle\\&=\sum_{k=0}^n\dbinom nk\langle h(t)\mid s_k(x)\rangle\langle l(t)\mid p_{n-k}(x)\rangle\end{aligned} \]

我们以一个例子来结束本节，来说明本影结果如何很好的与(产生适用于 Sheffer 序列的公式)结合起来 .

我们想要确定展开中的一组系数 \(a_{n,k}\)：

\[xs_n(x)=\sum_{k=0}^{n+1}a_{n,k}s_k(x) \]

其中 \(s_n(x)\) 是一个 Sheffer 序列 . 若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则由多项式展开定理，

\[xs_n(x)=\sum_{k=0}^{n+1}\dfrac{\langle g(t)f(t)^k\mid xs_n(x)\rangle}{k!}s_k(x) \]

综合使用一下之前的定理们：

\[\begin{aligned}\langle g(t)f(t)^k\mid xs_n(x)\rangle&=\langle g'(t)f(t)^k+kg(t)f(t)^{k-1}f'(t)\mid s_n(x)\rangle&\text{(Proposition 1.1.1)}\\&=\langle g'(t)\mid f(t)^ks_n(x)\rangle+k\langle g(t)f'(t)\mid f(t)^{k-1}s_n(x)\rangle&\text{(Theorem 1.2.1)}\\&=n^{\underline k}\langle g'(t)\mid s_{n-k}(x)\rangle+kn^{\underline{k-1}}\langle g(t)f'(t)\mid s_{n-k+1}(x)\rangle&\text{(Theorem 1.3.7)}\end{aligned} \]

这导出：

定理 1.3.11

若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则

\[xs_n(x)=\sum_{k=0}^{n+1}\left(\dbinom nk\langle g'(t)\mid s_{n-k}(x)\rangle+\dbinom n{k-1}\langle g(t)f'(t)\mid s_{n-k+1}(x)\rangle\right)s_k(x) \]

其中组合数 \(\binom mj\) 在 \(j<0\) 或 \(j>m\) 时为 \(0\) .

（这个展开式将在第 3 章被使用）

同样值得一提的是，用 \(s_k(x)\) 表示 \(s'_n(x)\) 的公式：

定理 1.3.12

若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，\(p_n(x)\) 相关于 \(f(t)\) . 则

\[s'_n(x)=\sum_{k=0}^{n-1}\dbinom nk\langle t\mid p_{n-k}(x)\rangle s_k(x) \]

证明：由多项式展开定理，

\[\begin{aligned}s'_n(x)&=\sum_{k=0}^{n-1}\dfrac{\langle g(t)f(t)^k\mid ts_n(x)\rangle}{k!}s_k(x)\\&=\sum_{k=0}^{n-1}\dfrac{\langle t\mid g(t)f(t)^ks_n(x)\rangle}{k!}s_k(x)\\&=\sum_{k=0}^{n-1}\dbinom nk\langle t\mid p_{n-k}(x)\rangle s_k(x)\end{aligned} \]

证明完毕 .

接下来我们将描述上述定理在两种特殊 Sheffer 序列（相关序列，Appell 序列）上的表现 .

4. 相关序列

本节除了定理 1.4.5 都是不需要特殊注意的 .

定理 1.4.1 (展开定理, The Expansion Theorem)

令 \(p_n(x)\) 相关于 \(f(t)\) . 则对于任意 \(h(t)\in\mathcal F\)，

\[h(t)=\sum_{k\ge0}\dfrac{\langle h(t)\mid p_k(x)\rangle}{k!}f(t)^k \]

定理 1.4.2 (多项式展开定理, The Polynomial Expansion Theorem)

令 \(p_n(x)\) 相关于 \(f(t)\) . 则对于任意 \(h(t)\in\mathcal F\)，

\[h(t)=\sum_{k\ge0}\dfrac{\langle f(t)^k\mid p(x)\rangle}{k!}p_k(x) \]

定理 1.4.3

序列 \(p_n(x)\) 相关于 \(f(t)\) 当且仅当

\[\mathrm e^{yf^\I(t)}=\sum_{k\ge0}\dfrac{p_k(y)}{k!}t^k \]

对于每个 \(y\in\mathbb C\) 成立 .

定理 1.4.4

序列 \(p_n(x)\) 相关于 \(f(t)\) 当且仅当

\[p_n(x)=\sum_{k=1}^n\dfrac{\langle f^\I(x)^k\mid x^n\rangle}{k!}x^k \]

这被称为相关序列的共轭表示 .

相关序列的算子表示相对于 Sheffer 序列来说有一个新的性质：

定理 1.4.5

序列 \(p_n(x)\) 相关于 \(f(t)\) 当且仅当

1. \(\langle t^0\mid p_n(x)\rangle=[n=0]\) .
2. \(f(t)p_n(x)=np_{n-1}(x)\) .

证明：充分性显然，考虑必要性 . 假设 1, 2 都成立，则

\[\begin{aligned}\langle f(t)^k\mid p_n(x)\rangle&=\langle t^0\mid f(t)^kp_n(x)\rangle\\&=\langle t^0\mid n^{\underline k}p_{n-k}(x)\rangle\\&=n^{\underline k}[n-k]=0\\&=n![n=k]\end{aligned} \]

而 1 意味着 \(p_0(x)=1\) 且对于 \(n>0\) 有 \(p_n(0)=0\)，从而使用定理 1.3.7 即可完成证明 .

定理 1.4.6

令 \(p_n(x)\) 相关于 \(f(t)\) . 则对于任意 \(h(t)\in\mathcal F\)，

\[h(t)p_n(x)=\sum_{k=0}^n\dbinom nk\langle h(t)\mid p_k(x)\rangle p_{n-k}(x) \]

定理 1.4.7 (二项恒等式, The Binomial Identity)

序列 \(p_n(x)\) 相关于 \(f(t)\) 当且仅当

\[p_n(x+y)=\sum_{k=0}^n\dbinom nkp_k(y)p_{n-k}(x) \]

对于每个 \(y\in\mathbb C\) 成立 .

一个序列 \(p_n(x)\) 若满足二项恒等式，则它被称为二项型 (binomial type) 的 . 根据定理 1.4.7，一个序列是相关序列当且仅当它是二项型的 .

定理 1.4.8

若 \(p_n(x)\) 相关于 \(f(t)\)，则

\[xp_n(x)=\sum_{k=1}^{n+1}\dbinom n{k-1}\langle f'(t)\mid p_{n-k+1}(x)\rangle p_k(x) \]

定理 1.4.9

若 \(p_n(x)\) 是相关序列，则

\[p'_n(x)=\sum_{k=0}^{n-1}\dbinom nk\langle t\mid p_{n-k}(x)\rangle p_k(x) \]

5. Appell 序列

本节除了定理 1.5.10 都是不需要特殊注意的 .

定理 1.5.1 (展开定理, The Expansion Theorem)

令 \(s_n(x)\) Appell 于 \(g(t)\) . 则对于任意 \(h(t)\in\mathcal F\)，

\[h(t)=\sum_{k\ge0}\dfrac{\langle h(t)\mid s_k(x)\rangle}{k!}g(t)t^k \]

定理 1.5.2 (多项式展开定理, The Polynomial Expansion Theorem)

令 \(s_n(x)\) Appell 于 \(g(t)\) . 则对于任意多项式 \(p(x)\)，

\[p(x)=\sum_{k\ge0}\dfrac{g(t)\mid p^{(k)}(x)}{k!}s_k(x) \]

定理 1.5.3

序列 \(s_n(x)\) Appell 于 \(g(t)\) 当且仅当

\[\dfrac1{g(t)}\mathrm e^{yt}=\sum_{k\ge0}\dfrac{s_k(y)}{k!}t^k \]

对于每个 \(y\in\mathbb C\) 成立 .

定理 1.5.4

序列 \(s_n(x)\) Appell 于 \(g(t)\) 当且仅当

\[s_n(x)=\sum_{k=0}^n\dbinom nk\langle g(t)^{-1}\mid x^{n-k}\rangle x^k \]

这被称为 Appell 序列的共轭表示 .

定理 1.5.5

序列 \(s_n(x)\) Appell 于 \(g(t)\) 当且仅当

\[s_n(x)=g(t)^{-1}x^n \]

定理 1.5.5

序列 \(s_n(x)\) Appell 于 \(g(t)\) 当且仅当

\[ts_n(x)=ns_{n-1}(x) \]

也即 \(s'_n(x)=ns_{n-1}(x)\) .

在文献中关于 Appell 序列的一种常见定义是 \(u'_n(x)=u_{n-1}(x)\)，此处 \(n!u_n(x)\) 即为本文所描述的 Appell 序列 .

定理 1.5.7

令 \(s_n(x)\) Appell 于 \(g(t)\) . 则对于任意 \(h(t)\in\mathcal F\)，

\[h(t)s_n(x)=\sum_{k=0}^n\dbinom nk\langle h(t)\mid s_k(x)\rangle x^{n-k} \]

定理 1.5.8 (Appell 恒等式, The Appell Identity)

序列 \(s_n(x)\) 是 Appell 序列当且仅当

\[s_n(x+y)=\sum_{k=0}^n\dbinom nks_k(y)x^{n-k} \]

定理 1.5.9

若 \(s_n(x)\) Appell 于 \(g(t)\)，则

\[xs_n(x)=s_{n+1}(x)+\sum_{k=0}^n\dbinom nk\langle g'(t)\mid s_{n-k}(x)\rangle s_k(x) \]

定理 1.5.10 (乘法定理, The Multiplication Theorem)

若 \(s_n(x)\) Appell 于 \(g(t)\)，则对任意常数 \(\alpha\neq0\),

\[s_n(\alpha x)=\alpha^n\dfrac{g(t)}{g(t/\alpha)}s_n(x) \]

对每个 \(n\ge0\) 成立 .

证明：首先由性质 1.1.1 知 \(\langle f(t)\mid p(x)\rangle=\langle f(t/\alpha)\mid p(\alpha x)\rangle\)，从而有：

\[\begin{aligned}\langle t^k\mid g(t/\alpha)s_n(\alpha x)\rangle&=\langle\alpha^kt^kg(t)\mid s_n(x)\rangle\\&=\alpha^kn![n=k]\\&=\alpha^nn![n=k]\\&=\langle t^k\mid\alpha^ng(t)s_n(x)\rangle\end{aligned} \]

这指出 \(g(t/\alpha)s_n(\alpha x)=\alpha^ng(t)s_n(x)\)，从而也导出了命题 .

6. 一些例子

我们在此稍作停顿，来罗列一些 Sheffer 序列的例子 . 这里不会提供任何证明或动机，详细解释将在第 3 章介绍 .

尽管从接下来的讨论中可以看出，在某些情况下，计算一对线性泛函的 Sheffer 序列确实是间接的，但在下一章中我们将给出 Sheffer 序列的显式计算公式 .

可以参考 1.1 节的线性泛函例子和 1.2 节的线性算子例子 .

1. 序列 \(p_n(x)=x^n\)，相关于 delta 泛函 \(f(t)=t\) .

   其生成函数

   \[\sum_{k\ge0}\dfrac{x^k}{k!}t^k=\mathrm e^{xt} \]

   和二项式恒等式

   \[(x+y)^n=\sum_{k=0}^n\dbinom nkx^ky^{n-k} \]

   是不出乎意料的 .

2. 下降幂多项式 \(p(x)=x^{\underline n}\)，相关于前向差分泛函 \(f(t)=\mathrm e^t-1\)（可由定理 1.4.5 简单导出）.

   其生成函数

   \[\sum_{k\ge0}\dfrac{x^{\underline k}}{k!}t^k=\mathrm e^{x\log(1+t)} \]

   等价于二项式展开

   \[\sum_{k\ge0}\dbinom xkt^k=(1+t)^x \]

   其二项式恒等式

   \[(x+y)^{\underline n}=\sum_{k=0}^n\dbinom nkx^{\underline k}y^{\underline{n-k}} \]

   是下降幂二项式定理（等价于 Vandermonde 卷积）.

3. Abel 多项式 \(A_n(x;a)=x(x-an)^{n-1}\)，相关于 Abel 泛函 \(f(t)=t\mathrm e^{at}\)（仍然可由定理 1.4.5 简单导出）.

   其生成函数为

   \[\sum_{k\ge0}\dfrac{x(x-ak)^{k-1}}{k!}t^k=\mathrm e^{xf^\I(t)} \]

   顺便一提，如果在此处对 \(x\) 微分：

   \[\sum_{k\ge0}\dfrac{k(x-a)(x-ak)^{k-1}}{k!}t^k=f^\I(t)\mathrm e^{xf^\I(t)} \]

   取 \(x=0\) 即得 \(f\) 的复合逆：

   \[\sum_{k\ge1}\dfrac{(-a)^kk^{k-1}}{(k-1)!}t^k=f^\I(t) \]

   其二项式恒等式

   \[(x+y)(x-y-an)^{n-1}=\sum_{k=0}^n\dbinom nkxy(x-ak)^{k-1}(y-a(n-k))^{n-k-1} \]

   这是一个由 Abel 得出的公式 .

4. Hermite 多项式 \(H_n(x)\)，Appell 于 \(g(t)=\mathrm e^{t^2/2}\) . 由定理 1.5.5 可知

   \[\begin{aligned}H_n(x)&=\mathrm e^{-t^2/2}x^n\\&=\sum_{k=0}^x\left(-\dfrac12\right)^k\dfrac1{k!}t^{2k}x^n\\&=\sum_{k\ge0}\left(-\dfrac12\right)^k\dfrac{n^{\underline{2k}}}{k!}x^{n-k}\end{aligned} \]

   其生成函数

   \[\sum_{k=0}^x\dfrac{H_k(x)}{k!}t^k=\mathrm e^{-t^2/2}\mathrm e^{xt}=\mathrm e^{xt-t^2/2} \]

   其 Appell 恒等式

   \[H_n(x+y)=\sum_{k=0}^n\dbinom nkH_k(x)y^{n-k} \]

   注意：Hermite 多项式通常指代满足

   \[\sum_{k\ge0}\dfrac{s_k(x)}{k!}=\mathrm e^{2xt-t^2} \]

   的序列 \(s_n(x)\) . 它并非精确的 Appell 序列，而 Sheffer 于 \((\mathrm e^{t^2/4},t/2)\) .

   在第 3 章将会讨论关于变量 \(v\) 的广义 Hermite 多项式 \(H^{(v)}_n(x)\) .

5. Bernoulli 多项式 \(B_n(x)\)，Appell 于 \(g(t)=(\mathrm e^{t}-1)/t\) . 由定理 1.5.5 可知

   \[B_n(x)=\dfrac{tx}{\mathrm e^{t}-1} \]

   其生成函数为

   \[\sum_{k\ge0}\dfrac{B_k(x)}{k!}t^k=\dfrac{t\mathrm e^{xt}}{\mathrm e^{t}-1} \]

   取 \(x=0\) 即得 Bernoulli 数的生成函数

   \[\sum_{k\ge0}\dfrac{B_k(0)}{k!}t^k=\dfrac{t}{\mathrm e^{t}-1} \]

   在第 3 章将会讨论关于序为 \(\alpha\) 的广义 Bernoulli 多项式 \(B^{(\alpha)}_n(x)\) .

6. \(\alpha\) 阶的 Laguerre 多项式 \(L_n^{(\alpha)}(x)\)，Sheffer 于 \((t/(t-1),(1-t)^{-\alpha-1})\) . 特别的，序列 \(L^{(-1)}_n\) 相关于 \(f(t)=t/(t-1)\) .

   通过下一章的公式我们可以简单计算得到

   \[L_n^{(\alpha)}=\sum_{k=0}^n\dfrac{n!}{k!}\dbinom{\alpha+n}{n-k}(-x)^k \]

   其生成函数为

   \[\sum_{k\ge0}\dfrac{L_k^{(\alpha)}(x)}{k!}t^k=\dfrac{\mathrm e^{xt/(t-1)}}{(1-t)^{\alpha+1}} \]

   其 Sheffer 恒等式为

   \[L_n^{(\alpha)}(x+y)=\sum_{k=0}^n\dbinom nkL_k^{(\alpha)}(x)L_{n-k}^{(-1)}(y) \]

   关于 Laguerre 多项式，很多有趣的由本影法得出的结论源于结论 \(f^\I(t)=f(t)\) .

   再一次，需要注意其他文献中通常 Laguerre 多项式被定义为 \(L^{(\alpha)}_n(x)/n!\) . 另外，由正交性，有时会限制 \(\alpha>-1\)（不必多说，我们将不理会这个限制）.

2. 算子及其伴随

1. \(\mathbb P^*\) 上的连续算子

现在重命名本影代数 \(\mathcal F\) 为 \(\mathbb P^*\)，暂时我们将只关心本影代数的向量空间结构 .

\(\mathbb P^*\) 上的线性算子 \(T\) 的一个重要性质是它在无穷求和上的表现：

\[T\sum_{k\ge0}a_kf_k(t)=\sum_{l\ge0}a_kTf_k(t) \]

其中 \(\sum_{k\ge0}a_kf_k(t)\) 存在，也即 \(k\to\infty\) 时 \(\ord(f_k(t))\to\infty\) . 同时要使式子有意义，等号右边也必须存在，也即 \(k\to\infty\) 时 \(\ord(Tf_k(t))\to\infty\) . 那么可以导出性质成立的一个必要条件：

\[\ord(f_k(t))\to\infty\text{ whenever } \ord(Tf_k(t))\to\infty\tag{1} \]

这已经足够了：

定理 2.1.1

如果 \(T\) 是 \(\mathbb P^*\) 上的，满足 \((1)\) 的线性算子，则

\[T\sum_{k\ge0}a_kf_k(t)=\sum_{l\ge0}a_kTf_k(t) \]

对于所有 \(k\to 0\) 时 \(\ord(f_k(t))\to\infty\) 的序列 \(f_k(t)\) 成立 .

假定 \(\ord(f_k(t))\to\infty\)，则对于任意多项式 \(p(x)\) 和 \(m\ge 0\)：

\[\left\langle T\sum_{k\ge0}a_kf_k(t)\Lmid p(x)\right\rangle=\left\langle T\sum_{k=0}^ma_kf_k(t)\Lmid p(x)\right\rangle+\left\langle T\sum_{k\ge m+1}a_kf_k(t)\Lmid p(x)\right\rangle \]

现在 \(\ord(f_k(t))\to\infty\) 蕴含当 \(m\to\infty\) 时 \(\ord(\sum_{k\ge m+1}a_kf_k(t))\to\infty\)，也即 \(m\to\infty\) 时 \(\ord(T\sum_{k\ge m+1}a_kf_k(t))\to\infty\) . 从而可以令 \(m\) 足够大让右侧第二项消失且 \(k>m\) 时 \(\ord(Tf_k(t))>\deg p(x)\)，

\[\begin{aligned}\left\langle T\sum_{k\ge0}a_kf_k(t)\Lmid p(x)\right\rangle&=\left\langle T\sum_{k=0}^ma_kf_k(t)\Lmid p(x)\right\rangle\\&=\left\langle\sum_{k=0}^ma_k Tf_k(t)\Lmid p(x)\right\rangle\\&=\left\langle\sum_{k=0}^{\infty}a_k Tf_k(t)\Lmid p(x)\right\rangle\end{aligned} \]

命题得证！

称 \(\mathbb P^*\) 上的线性算子 \(T\) 是连续的当且仅当其满足 \((1)\) .

实际上，可以通过指定当对于任意 \(n\ge0\) 都存在整数 \(k_n\) 使得当 \(k>k_m\) 时 \(f_k(t)\) 和 \(f(t)\) 的前 \(n\) 项一样（形式化的，对于 \(0\le j<n\)，\(\langle f_k(t)\mid x^j\rangle=\langle f(t)\mid x^j\rangle\)）时，序列 \(f_k(t)\) 收敛于 \(f(t)\) 定义 \(\mathbb P^*\) 上的一个拓扑，这使 \(\mathbb P^*\) 变为一个拓扑向量空间 . 显然，\(f_k(t)\) 收敛于 \(0\) 当且仅当 \(k\to\infty\) 时 \(\ord(f_k(t))\to\infty\)，从而一个线性算子 \(T\) 是连续的当且仅当 \(Tf_k(t)\) 收敛到 \(0\) 每当 \(f_k(t)\) 收敛到 \(0\) . 因为实际上我们不需要任何除连续性之外的拓扑概念，所以我们还是保留 \((1)\) 作为连续的定义 .

2. \(\mathbb P^*\) 上的自同构和导子

我们特此声明并确认，线性算子 \(T\) 是 \(\mathbb P^*\) 上的代数态射当且仅当它保持 \(\mathbb P^*\) 上的乘法：

\[T(f(t)g(t))=Tf(t)Tg(t) \]

此外，如果 \(T\) 是双射，则称其为 \(\mathbb P^*\) 上的自同构 .

定理 2.2.1

若 \(T\) 是 \(\mathbb P^*\) 上的自同构，那么它保序，也即 \(\ord(Tf(t))=\ord(f(t))\) 对每个 \(f(t)\in\mathbb P^*\) 成立 .

注意到 \(Tf(t)\) 可逆当且仅当 \(f(t)\) 可逆：若 \(f(t)\) 可逆，则 \(Tf(t)T(f(t)^{-1})=T(f(t)f(t)^{-1})=T1=1\)，从而 \(Tf(t)\) 可逆，反之亦然 .

在序的方面有 \(\ord(Tf(t))=0\) 当且仅当 \(\ord(f(t))=0\) . 特殊的，\(\ord(Tt)\ge1\)，但如果 \(\ord(Tt)>1\) 将不存在 \(g(t)\in\mathbb P^*\) 使得 \(Tg(t)=t\) . 可以将任意 \(g(t)\in\mathbb P^*\) 写为 \(g(t)=g_0+tg_1(t)\) 的形式，进而 \(Tg(t)=g_0+T(tg_1(t))\neq t\)，因为 \(\ord(Ttg_1(t))=\ord(TtTg_1(t))\ge \ord(Tt)>1\). 从而，如果 \(T\) 是满射，必有 \(\ord(Tt)=1\) . 这蕴含对于 \(k\ge0\) 有 \(\ord(Tt^k)=k\) . 那么如果 \(\ord(f(t))=k\)，则 \(f(t)=t^kg(t)\) 其中 \(\ord(g(t))=0\)，则 \(\ord(Tf(t))=\ord(Tt^kTg(t))=\ord(Tt^k)+\ord(Tg(t))=k\) .

推论 2.2.1

任何 \(\mathbb P^*\) 上的自同构都是连续的 .

因此，可以注意到任何一个自同构由它在任意一个 delta 泛函上的值唯一确定，特别是它在 \(t\) 上的值 .

线性算子 \(\partial\) 是 \(\mathbb P^*\) 上的导子当且仅当

\[\partial(f(t)g(t))=f(t)\partial g(t)+g(t)\partial f(t) \]

对所有 \(\mathbb P^*\) 内的 \(f(t),g(t)\) 成立 .

定理 2.2.2

若 \(\partial\) 是 \(\mathbb P^*\) 上的满射导子，则对于任意常数 \(c\in \mathbb C\) 有 \(\partial c=0\)，且 \(\ord(\partial f(t))=k-1\) 每当 \(\ord(f(t))=k\ge1\) .

考虑到 \(\partial 1=\partial 1^2=\partial 1+\partial 1\)，所以 \(\partial 1=0\)，那么对于任意常数 \(c\) 都有 \(\partial c=0\) .

同样将任意 \(g(t)\in\mathbb P^*\) 写为 \(g(t)=g_0+tg_1(t)\) 的形式，则 \(\partial g(t)=t\partial g_1(t)+g_1(t)\partial t\)，并且由 \(\ord(t\partial g_1(t))\ge1\) 且 \(\partial\) 是满射可以导出 \(\ord(\partial t)=0\) . 从而如果 \(\ord(f(t))=k\ge1\)，则 \(f(t)=t^kg(t)\) 其中 \(\ord(g(t))=0\)，进而 \(\ord(\partial f(t))=\ord(t^k\partial g(t)+kt^{k-1}g(t)\partial t)=k-1\) .

推论 2.2.2

任何 \(\mathbb P^*\) 上的导子都是连续的 .

3. 伴随

若 \(\lambda\) 是 \(\mathbb P\) 上的线性算子，则其伴随 \(\lambda^*\) 是 \(\mathbb P^*\) 上的线性算子，其中对于每个 \(f(t)\in\mathbb P^*\)：

\[\langle \lambda^*f(t)\mid p(x)\rangle=\langle f(t)\mid \lambda p(x)\rangle\tag2 \]

对于每个多项式 \(p(x)\) 成立 .

例如，因为 \(\langle f(t)g(t)\mid p(x)\rangle=\langle g(t)\mid f(t)p(x)\rangle\)，可以发现算子 \(\lambda=f(t)\) 的伴随是它对 \(f(t)\) 的算子乘积，也即 \(f(t)^*g(t)=f(t)g(t)\) 对于每个 \(g(t)\in\mathbb P^*\) 成立 .

由 \((2)\) 可以简单导出伴随的几个性质：

• \((\lambda+\mu)^*=\lambda^*+\mu^*\) .
• \((c\lambda)^*=c\lambda^*\) .
• \((\lambda\circ\mu)^*=\mu^*\circ\lambda^*\) .
• 对于可逆的 \(\lambda\)，\((\lambda^{-1})^*=(\lambda^*)^{-1}\) .

因此，将 \(\mathbb P\) 上的线性算子 \(\lambda\) 发送到它的伴随——\(\mathbb P^*\) 上的线性算子 \(\lambda^*\) 的伴随映射是一个从向量空间 \(\mathbb P\) 上的每个线性算子到向量空间 \(\mathbb P^*\) 上的每个线性算子的线性变换 . 进而，若 \(\lambda^*=0\)，则对于每个 \(f(t)\in\mathbb P^*,\,p(x)\in\mathbb P\) 有 \(\langle f(t)\mid\lambda p(x)\rangle=0\)，从而 \(\lambda=0\)，也即伴随映射是单射 . 在下一个定理中我们将确定它的范围：

定理 2.3.1

\(\mathbb P^*\) 上的线性算子 \(T\) 是某个 \(\mathbb P\) 上的线性算子 \(\lambda\) 的伴随，当且仅当 \(T\) 是连续的 .

充分性：假定 \(T=\lambda^*\) 对某些 \(\mathbb P\) 上的线性算子成立，且 \(\ord(f_k(t))\to\infty\) .

则对于所有 \(n\ge0\) 存在整数 \(k_n\) 使得 \(k>k_n\) 蕴含 \(\ord(f_k(t))>\deg\lambda x^j\) 对于 \(0\le j\le n\) 成立，也即 \(\ord(Tf_k(t))>n\) . 则 \(\ord(Tf_k(t))\to\infty\)，\(T\) 是连续的 .

必要性：若 \(T\) 是连续的，则取 \(\mathbb P\) 上的线性算子 \(\lambda\)：

\[\lambda x^n=\sum_{k\ge0}\dfrac{\langle Tt^k\mid x^n\rangle}{k!}x^k \]

因为 \(k\) 足够大时 \(\ord(Tt^k)>n\)，所以求和是有限的，从而

\[\begin{aligned}\langle\lambda^*t^m\mid x^n\rangle&=\langle t^m\mid\lambda x^n\rangle\\&=\sum_{k\ge0}\dfrac{\langle Tt^k\mid x^n\rangle}{k!}\langle t^m\mid x^k\rangle\\&=\langle Tt^m\mid x^n\rangle\end{aligned} \]

从而对于每个 \(m\ge0\) 有 \(\lambda^*t^m=Tt^m\)，因为 \(\lambda\) 和 \(T\) 都是连续的，从而 \(\lambda^*f(t)=Tf(t)\) 对于每个 \(f(t)\in\mathbb P^*\) 成立，那么 \(T=\lambda^*\) .

证明完毕 .

总之，可以确定如下定理：

定理 2.3.2

伴随映射（将 \(\mathbb P\) 上的线性算子 \(\lambda\) 发送到……）是一个从 \(\mathbb P\) 上的所有线性算子到 \(\mathbb P^*\) 上的所有连续线性算子的向量空间同构 .

由于自同构和导子都是连续的，所以可以先把右边填上两类连续算子：

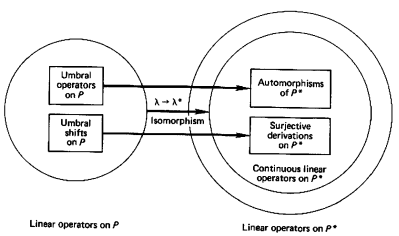
关于左边填的算子（本影算子和本影移位）将在后面的章节进行介绍，不过这里会先处理一些其它的结果 .

如果 \(T\) 是 \(\mathbb P^*\) 上的线性算子，他也有一个定义在 \(\mathbb P^{**}\) 上的伴随 \(T^*\)，其满足：

\[(T^*\phi)f(t)=\phi(Tf(t)) \]

对于每个 \(\phi\in\mathbb P^{**}\) 和 \(f(t)\in\mathbb P^*\) 成立 .

注意：向量空间 \(\mathbb P\) 和 \(\mathbb P^{**}\) 不是同构的，存在一个从 \(\mathbb P\) 射入 \(\mathbb P^{**}\) 的向量空间同构 \(\theta\)（通常被称为典范同构）：

\[(\theta p(x))f(t)=\langle f(t)\mid p(x)\rangle \]

对于每个 \(f(t)\in\mathbb P^*,\,p(x)\in\mathbb P\) 成立 . 或者可以看成把多项式 \(p(x)\) 看成 \(\mathbb P^*\) 上的线性泛函：\(p(x)f(t)=\langle f(t)\mid p(x)\rangle\) .

如果 \(T\) 是线性算子，自然可以想到考虑伴随 \(T^*:\mathbb P^{**}\to \mathbb P^{**}\) 是否将 \(\mathbb P^{**}\) 上的多项式映射到 \(\mathbb P^{**}\) 上的多项式，也即是否有 \(T^*\theta(\mathbb P)\subset \theta(\mathbb P)\) .

定理 2.3.3

\(T\) 是 \(\mathbb P^*\) 上的线性算子，则伴随 \(T^*\) 满足 \(T^*\theta(\mathbb P)\subset\theta(\mathbb P)\) 当且仅当 \(T\) 是连续的 .

充分性：假定 \(T^*\theta(\mathbb P)\subset\theta(\mathbb P)\) 且令 \(\ord(f_k(t))\to\infty\) . 则对于每个 \(j\ge0\) 有 \(\theta^{-1}T\theta x^j\in\mathbb P\)，且对于每个 \(n\ge 0\) 存在整数 \(k_n\) 使得 \(k>k_n\) 蕴含对于每个 \(0\le j\le n\) 有 \((T^*\theta x^j)f_k(t)=\langle f_k(t)\mid\theta^{-1}Tx^j\rangle=0\)，也即 \(k>k_n\) 蕴含对于每个 \(0\le j\le n\) 有 \(\langle Tf_k(t)\mid x^j\rangle=(\theta x^j)(Tf_k(t))=(T^*\theta x^j)f_k(t)=0\)，也即 \(\ord(Tf_k(t))>n\)，从而 \(T\) 是连续的 .

必要性：假定 \(T\) 是连续的，则对于某个 \(\mathbb P\) 上的算子 \(\lambda\) 有 \(T=\lambda^*\)，则：

\[\begin{aligned}(T^*\theta p(x))(f(t))&=(\lambda^{**}\theta p(x))f(t)\\&=(\theta p(x))(\lambda^*f(t))\\&=\langle\lambda^*f(t)\mid p(x)\rangle\\&=\langle f(t)\mid \lambda p(x)\rangle\\&=(\theta\lambda p(x))f(t)\end{aligned} \]

从而 \(T^*\theta p(x)=\theta\lambda p(x),\,T^*\theta=\theta\lambda\)，从而 \(T^*\theta(\mathbb P)=\theta\lambda(\mathbb P)\subset\theta(\mathbb P)\) .

证明完毕 .

4. 本影算子和本影复合

把本影代数的名字改回 \(\mathcal F\) .

\(p_n(x)\) 是 \(f(t)\) 的相关序列，则关于 \(p_n(x)\) 或 \(f(t)\) 的本影算子是 \(\mathbb P\) 上的满足 \(\lambda x^n=p_n(x)\) 的线性算子 \(\lambda\) .

为了表明 \(\lambda\) 对 \(f(t)\) 的相关性，可能会使用记号 \(\lambda_f\) .

因为 \(\deg p_n(x)=n\)，所以显然本影算子是双射 .

在本节中，我们打算通过其伴随来表征本影算子 . 由定理 2.3.1，本影算子的伴随是连续的 . 然而事实远不仅如此，因为如果 \(\lambda_f:x^n\to p_n(x)\) 是本影算子，则：

\[\begin{aligned}\langle\lambda_f^*f(t)^k\mid x^n\rangle&=\langle f(t)^k\mid \lambda_fx^n\rangle\\&=\langle f(t)^k\mid p_n(x)\rangle\\&=n![n=k]\\&=\langle t^k\mid x^n\rangle\end{aligned} \]

从而对于每个 \(k\ge0\) 有 \(\lambda_f^*f(t)^k=t^k\)，由连续性可得对于每个 \(g(t)\in\mathcal F\) 有 \(\lambda_f^*g(f(t))=g(t)\) .

特别的，取 \(g(t)=f^\I(t)^k\)，则得到 \(\lambda_f^*t^k=f^\I(t)^k\)，这导出对于每个 \(g(t)\in\mathcal F\) 有 \(\lambda^*g(t)=g(f^\I(t))\) . 也即 \(\lambda_f\) 的效果是代入 \(f^\I(t)\) .

再推一下可以进一步得到 \(\lambda_f^*(g(t)h(t))=g(f^\I(t))h(f^\I(t))=\lambda_f^*h(t)\lambda_f^*h(t)\)，从而 \(\lambda_f^*\) 是 \(\mathbb P\) 上的自同构 .

定理 2.4.1

\(\mathbb P\) 上的线性算子 \(\lambda\) 是本影算子当且仅当其伴随 \(\lambda^*\) 是 \(\mathcal F\) 上的自同构 . 进而，若 \(\lambda_f\) 是本影算子，则对于每个 \(g(t)\in\mathcal F\)，\(\lambda_f^*g(t)=g(f^\I(t))\) . 特殊的，\(\lambda_f^*f(t)=t\) .

充分性已经证过，只需证必要性 . 假定 \(\lambda^*\) 是 \(\mathcal F\) 上的自同构，则根据定理 2.2.1 可知 \(\lambda^*\) 是双射，且存在唯一的 delta 级数 \(f(t)\) 使得 \(\lambda^*f(t)=t\) .

如果 \(p_n(x)\) 相关于 \(f(t)\)，则：

\[\begin{aligned}\langle f(t)^k\mid \lambda x^n\rangle&=\langle\lambda^*f(t)^k\mid x^n\rangle\\&=\langle t^k\mid x^n\rangle\\&=n![n=k]\\&=\langle f(t)^k\mid p_n(x)\rangle\end{aligned} \]

从而 \(\lambda x^n=p_n(x)\)，也即 \(\lambda\) 是本影算子 . 证明完毕 .

推论 2.2.1、定理 2.3.1 和定理 2.4.1 表明本影算子的伴随确实是 \(\mathcal F\) 上的自同构，那么可以确定伴随映射图片的左上角方框：

定理 2.4.2

伴随映射（将 \(\mathbb P\) 上的线性算子 \(\lambda\) 发送到……）是一个从 \(\mathbb P\) 上的所有本影算子和 \(\mathcal F\) 上的所有自同构间的双射 .

那么可以简单看穿自同构关于算子复合构成一个群：

定理 2.4.3

\(\mathbb P\) 上的所有本影算子在复合下构成群，事实上：

\[\lambda_f\circ\lambda_g=\lambda_{g\circ f}\qquad\qquad\lambda_f^{-1}=\lambda_{f^\I} \]

第一种证明：令 \(\lambda,\mu\) 是本影算子，则 \((\lambda\circ\mu)^*=\mu^*\circ\lambda^*\) 是 \(\mathcal F\) 上的自同构 . 由定理 2.4.2 得 \(\lambda\circ\mu\) 是本影算子 . 类似的，\((\lambda^{-1})^*=(\lambda^*)^{-1}\) 是 \(\mathcal F\) 上的自同构，所以 \(\lambda^{-1}\) 是本影算子 . 那么可以证明命题的第一部分 .

第二种证明：这种证明可以证得第二部分，但是没有那么优雅 .

\[\begin{aligned}(\lambda_f\circ\lambda_g)^*h(t)&=(\lambda_g^*\circ\lambda_f^*)h(t)\\&=f^\I(g^\I(t))\\&=(g\circ f)^\I(t)\\&=\lambda_{g\circ f}^*h(t)\end{aligned} \]

从而 \((\lambda_f\circ\lambda_g)^*=\lambda_{g\circ f}^*\)，也即 \(\lambda_f\circ\lambda_g=\lambda_{g\circ f}\) . 类似地，

\[(\lambda_f^{-1})^*h(t)=(\lambda_f^*)^{-1}h(t)=h(f(t))=\lambda_{f^\I}h(t) \]

从而 \(\lambda_f^{-1}=\lambda_{f^\I}\) .

推论 2.4.3 (1)

本影算子是相关序列到相关序列的映射 .

令 \(p_n(x)\) 是相关序列，\(\lambda\) 是本影算子 . \(\mu:x^n\to p_n(x)\) 是 \(p_n(x)\) 的本影算子，则有 \(\lambda p_n(x)=(\lambda\circ\mu)x^n\)，由于 \(\lambda\circ\mu\) 也是本影算子所以 \(\lambda p_n(x)\) 是相关序列 .

推论 2.4.3 (2)

如果 \(p_n(x),q_n(x)\) 是相关序列，且 \(\alpha:p_n(x)\to q_n(x)\) 是线性算子，则 \(\alpha\) 是本影算子 .

考虑 \(p_n(x),q_n(x)\) 的本影算子 \(\lambda:x^n\to p_n(x),\,\mu:x^n\to q_n(x)\)，则 \((\mu\circ\lambda^{-1})p_n(x)=q_n(x)=\alpha p_n(x)\)，从而 \(\alpha=\mu\circ\lambda^{-1}\)，自然是本影算子 .

考察定理 2.4.3 在相关序列上的表现，由定义，\(\lambda_{g\circ f}x^n\) 相关于 delta 泛函 \(g(f(t))\)，但是如果写成：

\[\begin{aligned}&\lambda_f:x^n\to p_n(x)\\&\lambda_g:x^n\to q_n(x)=\sum_{k=0}^nq_{n,k}x^k\end{aligned} \]

则：

\[\lambda_{g\circ f}x^n=(\lambda_f\circ \lambda_g)x^n=\lambda_fq_n(x)=\sum_{k=0}^nq_{n,k}p_k(x) \]

一般的，若 \(p_n(x)\) 和 \(q_n(x)=\sum_{k=0}^nq_{n,k}x^k\) 是多项式的序列，定义 \(q_n(x)\) 和 \(p_n(x)\) 的本影复合：

\[q_n(\mathbf p(x))=\sum_{k=0}^nq_{n,k}p_k(x) \]

可以转写为 \(\lambda_{g\circ f}x^n=q_n(\mathbf p(x))\) .

定理 2.4.4

相关序列在本影复合下构成群 . 特别的，若 \(p_n(x),q_n(x)\) 分别相关于 \(f(t),g(t)\)，则 \(q_n(\mathbf p(x))\) 相关于 \(g(f(t))\) . 本影复合下的单位元是序列 \(x^n\) . 序列 \(p_n(x)\) 的逆是 \(f^\I(t)\) 的相关序列 .

定理 2.4.5

\(\lambda\) 是 \(\mathbb P\) 上的本影算子，则作为 \(\mathbb P\) 上的算子，有

\[\lambda^* g(t)=\lambda^{-1}g(t)\lambda \]

对每个 \(g(t)\in\mathcal F\) 成立 .

对于任意 \(\mathcal f(t)\in\mathcal F,\,p(x)\in\mathbb P\)，有

\[\begin{aligned}\langle f(t)\mid(\lambda^*g(t))\mid p(x)\rangle&=\langle f(t)(\lambda^*g(t))\mid p(x)\rangle\\&=\langle \lambda^*(g(t)(\lambda^*)^{-1}f(t))\mid\mid p(x)\rangle\\&=\langle g(t)(\lambda^*)^{-1}f(t)\mid\lambda p(x)\rangle\\&=\langle(\lambda^{-1})^*f(t)\mid g(t)\lambda p(x)\rangle\\&=\langle f(t)\mid \lambda^{-1}g(t)\lambda p(x)\rangle\end{aligned} \]

也即 \(\lambda^*g(t)p(x)=\lambda^{-1}g(t)\lambda p(x)\)，\(\lambda^*g(t)=\lambda^{-1}g(t)\lambda\) .

从代入复合逆的角度看，这个定理相当于：

推论 2.4.5

对于任意本影算子 \(\lambda_f\)，有

\[\lambda_{f\circ g}(f^\I(t))=g(t)\circ\lambda_f \]

对每个 \(g(t)\in\mathcal F\) 成立 .

5. Sheffer 算子和本影复合

令 \(s_n(x)\) 是 \((g(t),f(t))\) 的 Sheffer 序列，则关于 \(s_n(x)\) 或 \((g(t),f(t))\) 的 Sheffer 算子是 \(P\) 上的满足 \(\lambda x^n=s_n(x)\) 的线性算子 \(\lambda\) . 显然 Sheffer 算子是双射 .

为了表明 \(\lambda\) 对 \(g(t),f(t)\) 的相关性，可能会使用记号 \(\lambda_{g,f}\) 或 \(\lambda_{g(t),f(t)}\) .

如果 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则 \(p_n(x)=g(t)s_n(x)\) 相关于 \(f(t)\)，则：

\[\lambda_{g,f}x^n=s_n(x)=g(t)^{-1}p_n(x)=g(t)^{-1}\lambda_x^n \]

也即 \(\lambda_{g,f}=g(t)^{-1}\lambda_f\) .

这让 Sheffer 算子的理论成本影算子理论的推论 . 特殊的，因为 \(\lambda_{g,f}^*=\lambda_f^*(g(t)^{-1})^*\)，所以对每个\(h(t)\in\mathcal F\) 有 \(\lambda_{g,f}^*h(t)=g(f^\I(t))^{-1}h(f^\I(t))\) .

定理 2.5.1

\(P\) 上的线性算子 \(\lambda\) 是 Sheffer 算子当且仅当其伴随 \(\lambda^*\) 有跟随 \(\mathcal F\) 上的自同构 \(\lambda_f^*\) 的可逆级数 \(g(t)^{-1}\) 的乘法形式 . 进而，若 \(\lambda^*\) 有这个形式，则 \(\lambda=\lambda_{g,f}\) . 事实上，任意 \(\mathcal F\) 上的有这个形式的算子都是 Sheffer 算子的伴随 .

考虑 Sheffer 算子的复合：

定理 3.5.2

所有 Sheffer 算子在复合下构成群，事实上：

\[\lambda_{g(t),f(t)}\circ\lambda_{h(t),l(t)}=\lambda_{g(t)h(f(t)),l(f(t))}\qquad\lambda_{g(t),f(t)}^{-1}=\lambda_{g(f^\I(t))^{-1},f^\I(t)} \]

对于本影算子 \(\lambda_{g(t),f(t)},\lambda_{h(t),l(t)}\)，

\[\begin{aligned}(\lambda_{g(t),f(t)}\circ\lambda_{h(t),l(t)})^*u(t)&=\lambda_{h(t),l(t)}^*\circ\lambda_{g(t),f(t)}^*u(t)\\&=h(l^\I(t))^{-1}g(f^\I(l^\I(t)))^{-1}u(f^\I(l^\I(t)))\\&=(h\circ f)((l\circ f)(t))^{-1}g((l\circ f)(t))^{-1}u((l\circ f)(t))\\&=\lambda_{h(f(t))g(t),l(f(t))}^*u(t)\end{aligned} \]

对于本影算子 \(\lambda_{g(t),f(t)}\)，

\[\begin{aligned}(\lambda_{g(t),f(t)}^{-1})^*u(t)&=(\lambda_f^{-1}\circ g(t))^*u(t)\\&=g(t)^*(\lambda_f^{-1})^*u(t)\\&=g(t)u(f(t))\\&=(g\circ f^\I)(f(t))u(f(t))\\&=\lambda_{g(f^\I(t))^{-1},f^\I(t)}^*u(t)\end{aligned} \]

推论 2.5.2 (1)

Sheffer 算子是 Sheffer 序列到 Sheffer 序列的映射 .

推论 2.5.2 (2)

如果 \(s_n(x),r_n(x)\) 是 Sheffer 序列，且 \(\alpha:s_n(x)\to r_n(x)\) 是线性算子，则 \(\alpha\) 是 Sheffer 算子 .

定理 2.5.3

Sheffer 序列在本影复合下构成群 . 特别的，若 \(s_n(x),r_n(x)\) 分别相关于 \((g(t),f(t)),(h(t),l(t))\)，则 \(r_n(\mathbf s(x))\) 相关于 \((g(t)h(f(t)),l(f(t)))\) . 本影复合下的单位元是序列 \(x^n\) . 序列 \(s_n(x)\) 的逆是 \((g(f^\I(t))^{-1},f^\I(t))\) 的 Sheffer 序列 .

以下是上面两章的一个总结：

定理 2.5.4

\(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则对于所有级数 \(h(t)\) 和多项式 \(q(x)\)，

\[\langle h(t)\mid q(\mathbf s(x))\rangle=\langle g(f^\I(t))^{-1}h(f^{\I}(x))\mid q(x)\rangle \]

特别的，

\[\langle h(t)\mid s_n(x)\rangle=\langle g(f^\I(t))^{-1}h(f^{\I}(x))\mid x^n\rangle \]

\(p_n(x)\) 相关于 \((g(t),f(t))\)，则对于所有级数 \(h(t)\) 和多项式 \(q(x)\)，

\[\langle h(t)\mid q(\mathbf p(x))\rangle=\langle h(f^\I(t))\mid q(x)\rangle \]

特别的，

\[\langle h(t)\mid p_n(x)\rangle=\langle h(f^\I(t))\mid x^n\rangle \]

6. 本影移位和相关序列的递推式

\(p_n(x)\) 是 \(f(t)\) 的相关序列，则关于 \(p_n(x)\) 或 \(f(t)\) 的本影移位是 \(\mathbb P\) 上的满足 \(\theta p_n(x)=p_{n+1}(x)\) 的线性算子 \(\theta\) .

因为同样的原因将会使用记号 \(\theta_f\) 来强调其与 \(f(t)\) 的依赖性 .

在下一节我们会学习到更一般的 Sheffer 移位：\(\theta:s_n(x)\to s_{n+1}(x)\) 对于任意 Sheffer 序列 \(s_n(x)\) .

因为 \(\deg p_n(x)=n\)，所以可以知道本影移位是单射，但不是满射 .

同样通过其伴随来描述本影移位，若 \(\theta_f:p_n(x)\to p_{n+1}(x)\) 是本影移位，则

\[\begin{aligned}\langle\theta_f^*f(t)^k\mid p_n(x)\rangle&=\langle f(t)^k\mid \theta_fp_n(x)\rangle\\&=\langle f(t)^k\mid p_{n+1}(x)\rangle\\&=(n+1)![n+1=k]\\&=kn![n=k-1]\\&=\langle kf(t)^{k-1}\mid p_n(x)\rangle\end{aligned} \]

也即对任意 \(k\ge0\)，有 \(\theta_f^*f(t)^k=kf(t)^{k-1}\) .

由展开定理，对于任意 \(g(t)\in\mathcal F\) 都能写成如下形式：

\[g(t)=\sum_{k\ge0}a_kf(t)^k \]

又由 \(\theta_f^*\) 的连续性

\[\theta_f^*g(t)=\sum_{k\ge0}ka_kf(t)^{k-1} \]

另一方面：

\[\begin{aligned}\theta_f^*f(t)^kf(t)^j&=\theta_f^*f(t)^{k+j}\\&=(k+j)\theta_f^*f(t)^{k+j-1}\\&=jf(t)^kf(t)^{j-1}+kf(t)^{k-1}f(t)^j\\&=f(t)^k\theta_f^*f(t)^j+f(t)^j\theta_f^*f(t)^k\end{aligned} \]

从而对于任意 \(g(t),h(t)\in\mathcal F\)，有

\[\theta_f^*g(t)h(t)=g(t)\theta_f^*h(t)+h(t)\theta_f^*g(t) \]

所以 \(\theta_f^*\) 是 \(\mathcal F\) 上的满射导子 . 容易发现映射 \(\theta_f^*\) 其实就是关于 \(f(t)\) 的导数 \(\partial_f\)，那么 \(\theta_f^*=\partial_f\) .

定理 2.6.1

\(\mathbb P\) 上的线性算子 \(\theta\) 是本影移位当且仅当其伴随 \(\theta^*\) 是 \(\mathcal F\) 上的满射导子 . 进而，若 \(\theta_f\) 是本影移位，则 \(\theta_f^*=\partial_f\) 是关于 \(f(t)\) 的导数，

\[\theta_f^*f(t)^k=kf(t)^{k-1} \]

对于每个 \(k\ge0\) 成立 . 特殊的，\(\theta_f^*f(t)=1\) .

充分性已证，必要性：若 \(\theta^*\) 是 \(\mathcal F\) 上的满射导子，则根据定理 2.2.2，存在 delta 泛函 \(f(t)\) 满足 \(\theta^*f(t)=1\) . 若 \(p_n(x)\) 相关于 \(f(t)\)，则

\[\begin{aligned}\langle f(t)^k\mid \theta p_n(x)\rangle&=\langle\theta^*f(t)^k\mid p_n(x)\rangle\\&=\langle kf(t)^{k-1}\theta^*f(t)\mid p_n(x)\rangle\\&=\langle kf(t)^{k-1}\mid p_n(x)\rangle\\&=\langle f(t)^k\mid p_{n+1}(x)\rangle\\&=(n+1)![n+1=k]\\&=\langle f(t)^k\mid p_{n+1}(x)\rangle\end{aligned} \]

所以 \(\theta p_n(x)=p_{n+1}(x)\)，\(\theta\) 是 \(f(t)\) 的本影移位 .

推论 2.2.2、定理 2.3.1 和定理 2.6.1 表明本影移位的伴随是 \(\mathcal F\) 上的满射导子，那么可以确定伴随映射图片的左下角方框：

定理 2.6.2

伴随映射（将 \(\mathbb P\) 上的线性算子 \(\lambda\) 发送到……）是一个从 \(\mathbb P\) 上的所有本影移位和 \(\mathcal F\) 上的所有满射导子间的双射 .

不同于自同构的情况，\(\mathcal F\) 上的满射导子组成的集合在复合下并不构成群 . 但是其复合关系是我们熟知的：

定理 2.6.3 (链式法则, The Chain Rule)

\(\partial_f,\partial_g\) 是 \(\mathcal F\) 上的满射导子，则

\[\partial_g=(\partial_g f(t))\partial_f \]

考虑到对于任意 \(k\ge0\)，

\[\partial_qf(t)^k=kf(t)^{k-1}\partial_gf(t)=(\partial_gf(t))\partial_ff(t)^k \]

接下来由连续性即可导出结论 .

推论 2.6.3

\(\partial_f,\partial_g\) 是 \(\mathcal F\) 上的满射导子，则

\[\partial_gf(t)=\dfrac1{\partial_fg(t)} \]

链式法则在本影移位上的表现：

定理 2.6.4

\(\theta_f,\theta_g\) 是本影移位，则

\[\theta_f=\theta_g\circ(\partial_fg(t)) \]

由链式法则：

\[\theta_f^*=(\partial_fg(t))\theta_g^* \]

所以

\[\begin{aligned}\langle h(t)\mid\theta_fp(x)\rangle&=\langle \theta_f^*h(t)\mid p(x)\rangle\\&=\langle(\partial_fg(t))\theta_g^*h(t)\mid p(x)\rangle\\&=\langle\theta_g^*h(t)\mid(\partial_fg(t))p(x)\rangle\\&=\langle h(t)\mid\theta_g\circ(\partial_fg(t))p(x)\rangle\end{aligned} \]

对于每个 \(h(t)\in\mathcal F,\,p(x)\in\mathbb P\)，于是 \(\theta_f=\theta_g\circ(\partial_f(g(t)))\) .

在定理 2.6.4 中取 \(g(t)=t\) 并注意到 \(\theta_gx^n=x^{n+1}\)（也即 \(\theta_g\) 是乘 \(x\) 算子），可以得到一个关于 \(\theta_f\) 的非常有用的公式：

\[\theta_f=x\partial_ft=x(\partial_ff(t))^{-1}=x(f'(t))^{-1} \]

将此应用于 \(f(t)\) 的相关序列则可以导出：

推论 2.6.4 (递推公式, The Recurrence Formulas)

若 \(p_n(x)\) 相关于 \(f(t)\)，则：

1. \(p_{n+1}(x)=x(f'(t))^{-1}p_n(x)\) .
2. \(p_{n+1}(x)=x\lambda_f(f^\I(t))'x^n\) .

1 已证，对于 2 使用推论 2.4.5：

\[p_{n+1}(x)=x(f'(t))^{-1}\lambda_fx^n=x\lambda_f(f'(f^\I(t)))^{-1}x^n=\lambda_f(f^\I(t))'x^n \]

顺便一提，递推公式的第二部分可以被写为

\[\lambda_fx^{n+1}=x\lambda_f(f^\I(t))'x^n \]

这等价于交换律

\[\lambda_fx=x\lambda_f(f^\I(x))' \]

我们现在可以得到一个关于 \(\mathcal F\) 上的满射导子的结论：

定理 2.6.5

\(\theta\) 是满射导子，则作为 \(p\) 上的算子有

\[\theta^*g(t)=g(t)\theta-\theta g(t) \]

对于所有 \(\mathcal F\) 上的算子成立 .

对于任意 \(f(t)\in\mathcal F,p(x)\in\mathbb P\)，

\[\begin{aligned}\langle f(t)\mid(\theta^*g(t))p(x)\rangle&=\langle f(t)(\theta^*g(t))\mid p(x)\rangle\\&=\langle\theta^*f(t)g(t)-g(t)\theta^*f(t)\mid p(x)\rangle\\&=\langle\theta^*f(t)g(t)\mid p(x)\rangle-\langle g(t)\theta^*f(t)\mid p(x)\rangle\\&=\langle f(t)\mid g(t)\theta p(x)\rangle-\langle f(t)\mid\theta g(t)p(x)\rangle\\&=\langle f(t)\mid(g(t)\theta-\theta g(t))p(x)\rangle\end{aligned} \]

当 \(\theta:x^n:x^{n+1}\) 是 \(p_n(x)=x^n\) 的本影移位时，映射 \(\theta^*\) 就是 \(\partial_t\)，而定理 2.6.5中的等式转为

\[g'(t)=g(t)x-xg(t) \]

其中两侧都作为 \(\mathbb P\) 上的算子考虑 . 右侧通常称 \(g(t)\) 的 Pincherle 导数 .

7. Sheffer 移位和 Sheffer 序列的递推式

\(s_n(x)\) 是 \((g(t),f(t))\) 的 Sheffer 序列，则关于 \(s_n(x)\) 或 \((g(t),f(t))\) 的 Sheffer 移位是 \(\mathbb P\) 上的满足 \(\theta s_n(x)=s_{n+1}(x)\) 的线性算子 \(\theta\) . 我们也使用记号 \(\theta_{g,f}\) .

同样由于 \(\deg s_n(x)=n\)，所以 Sheffer 移位是单射，但不是满射 .

若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则 \(p_n(x)=g(t)s_n(x)\) 相关于 \(f(t)\)，从而定义可以转为

\[\theta_{g,f}g(t)^{-1}p_n(x)=g(t)^{-1}p_{n+1}(x) \]

因此

\[\theta_{g,f}=g(t)^{-1}\theta_fg(t) \]

其中 \(\theta_f\) 是 \(f(t)\) 的本影移位 . 利用定理 2.6.4（的特殊情况）、定理 2.6.5 和链式法则可得：

\[\begin{aligned}\theta_{g,f}&=g(t)^{-1}\theta_fg(t)\\&=g(t)^{-1}(g(t)\theta_f-\theta_f^*g(t))\\&=\theta_f-g(t)^{-1}\partial_{f(t)}g(t)\\&=\theta_f-g(t)^{-1}\partial_{f(t)}t\partial_tg(t)\\&=x(f'(t))^{-1}-g(t)^{-1}(f'(t))^{-1}g'(t)\\&=\left(x-\dfrac{g'(t)}{g(t)}\right)\dfrac1{f'(t)}\end{aligned} \]

定理 2.7.1

\(\theta_{g,f}\) 是 Sheffer 移位，则

\[\theta_{g,f}=\left(x-\dfrac{g'(t)}{g(t)}\right)\dfrac1{f'(t)} \]

这给出了 Sheffer 序列的一个递推式：

推论 2.7.1 (Sheffer 序列的递推公式, The Recurrence Formula for Sheffer Sequences)

若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则

\[s_{n+1}(x)=\left(x-\dfrac{g'(t)}{g(t)}\right)\dfrac1{f'(t)}s_n(x) \]

8. 转换公式

接下来将得到两个关于由其 delta 泛函计算相关序列的强力的公式 . 这些公式与定理 1.3.2（展开定理）可被用于计算 Sheffer 序列 .

定理 2.8.1 (转换公式, The Transfer Formulas)

若 \(p_n(x)\) 是 \(f(t)\) 的相关序列，则对于每个 \(n\ge 0\)，

1. \(p_n(x)=f'(t)\left(\dfrac{f(t)}t\right)^{-n-1}x^n\) .
2. \(p_n(x)=x\left(\dfrac{f(t)}t\right)^{-n}x^{n-1}\) .

为了方便让 \(g(t)=f(t)/t\)，这样 \(g(t)\) 就是可逆的 . 事实上两个式子的右侧可以被证明相等，利用定理 2.6.5 的特殊情况，

\[\begin{aligned}f'(t)g(t)^{-n-1}x^n&=(tg(t))'g(t)^{-n-1}x^n\\&=g(t)^{-n}x^n+tg'(t)g(t)^{-n-1}x^n\\&=g(t)^{-n}x^n+ng'(t)g(t)^{-n-1}x^{n-1}\\&=g(t)^{-n}x^n-(g(t)^{-n})'x^{n-1}\\&=g(t)^{-n}x^n-(g(t)^{-n}x-xg(t)^{-n})x^{n-1}\\&=xg(t)^{-n}x^{n-1}\end{aligned} \]

为了证明 1，考虑对序列 \(q_n(x)=f'(t)g(t)^{-n-1}x^n\) 验证定理 1.4.5 中的两个条件：

1. 对于第一个条件，当 \(n\ge1\) 时利用上面第四个等号以及性质 1.1.1 可得
   \[\begin{aligned}\langle t^0\mid q_n(x)\rangle&=\langle t^0\mid g(t)^{-n}x^n-(g(t)^{-n})'x^{n-1}\mid q_n(x)\rangle\\&=\langle g(t)^{-n}\mid x^n\rangle-\langle(g(t)^{-n})'\mid x^{n-1}\rangle\\&=0\end{aligned} \]
   当 \(n=0\) 时 \(\langle t^0\mid q_n(x)\rangle=1\) . 所以 \(\langle t^0\mid q_n(x)\rangle=[n=0]\) .
2. 对于第二个条件
   \[\begin{aligned}f(t)q_n(x)&=f(t)f'(t)g(t)^{-n-1}x^n\\&=tg(t)f'(t)g(t)^{-n-1}x^n\\&=nf'(t)g(t)^{-n}x^{n-1}\\&=nq_{n-1}(x)\end{aligned} \]

从而 \(q_n(x)\) 相关于 \(f(t)\)，证明完毕 .

下面的推论给出了任意两个相关序列间的直接联系：

推论 2.8.1

若 \(p_n(x)\) 相关于 \(f(t)\)、\(q_n(x)\) 相关于 \(g(t)\)，则对于 \(n\ge1\)，

\[q_n(x)=x\left(\dfrac{f(t)}{g(t)}\right)^nx^{-1}p_n(x) \]

（\(f(t)/g(t)=(f(t)/t)(g(t)/t)^{-1}\) . 并且由于对于 \(n\ge1\)，\(p_n(0)=0\)，所以 \(x^{-1}p_n(x)\) 确实是多项式）.

由第一转换公式

\[(f(t)/t)^nx^{-1}p_n(x)=x^{n-1}=(g(t)/t)^nx^{-1}q_n(x) \]

整理即得原命题 .

我们以一个相当有用的结果结束这一节：

定理 2.8.2

若 \(s_n(x)\) Sheffer 于 \((g(t),f(t))\)，则

\[r_n(x)=s_n(x+\alpha+\beta n) \]

Sheffer 于

\[\left(g(t)\mathrm e^{-\alpha t}\left(1-\dfrac{\beta f(t)}{f'(t)}\right),\mathrm e^{-\beta t}f(t)\right) \]

序列 \(r_n(x)\) Sheffer 于 delta 泛函 \(\mathrm e^{-\beta t}f(t)\)，因为

\[\begin{aligned}\mathrm e^{-\beta t}f(t)r_n(x)&=\mathrm e^{-\beta t}f(t)\mathrm e^{(\alpha+\beta n)t}s_n(x)\\&=n\mathrm e^{(\alpha+\beta n-\beta)t}s_{n-1}(x)\\&=nr_{n-1}(x)\end{aligned} \]

现在假设 \(r_n(x)\) Sheffer 于 \((h(t),\mathrm e^{-\beta t}f(t))\) . 由推论 2.8.1 可知 \(\mathrm e^{-\beta t}f(t)\) 的相关序列

\[\begin{aligned}q_n(x)&=x\mathrm e^{\beta nt}x^{-1}p_n(x)\\&=\dfrac x{x+\beta n}p_n(x+\beta n)\\&=\mathrm e^{\beta nt}\left(\dfrac{x-\beta n}x\right)p_n(x)\end{aligned} \]

从而

\[h(t)s_n(x+\alpha+\beta n)=\mathrm e^{\beta nt}\left(\dfrac{x-\beta n}x\right)p_n(x) \]

\[h(t)s_n(x)=\mathrm e^{-\alpha t}\left(\dfrac{x-\beta n}x\right)p_n(x)=\mathrm e^{-\alpha t}(1-\beta nx^{-1})p_n(x) \]

由递推公式 \(p_n(x)=x(f'(t))^{-1}p_{n-1}(x)\)，

\[\begin{aligned}h(t)s_n(x)&=\mathrm e^{-\alpha t}(p_n(x)-\beta n(f'(t))^{-1}p_{n-1}(x))\\&=\mathrm e^{-\alpha t}(p_n(x)-\beta f(t)(f'(t))^{-1}p_n(x))\\&=\mathrm e^{-\alpha t}\left(1-\dfrac{\beta f(t)}{f'(t)}\right)p_n(x)\\&=\mathrm e^{-\alpha t}\left(1-\dfrac{\beta f(t)}{f'(t)}\right)g(t)s_n(x)\end{aligned} \]

证明完毕！