MMoE学习笔记：利用门控专家网络高效建模多任务关系

MMoE学习笔记：利用门控专家网络高效建模多任务关系

引言

多任务学习（Multi-Task Learning, MTL）已成为大规模推荐系统、计算广告等工业应用领域的标准技术范式。它旨在通过共享信息，利用相关任务中蕴含的知识来提升模型的学习效率和泛化能力。然而，传统的 MTL 方法，尤其是以 Shared-Bottom 为代表的硬参数共享架构，在处理任务间关系复杂或相关性较低的场景时，常常会遭遇“负迁移”（Negative Transfer）的困境，导致模型整体性能受损 。

为了解决这一难题，Google 的研究人员提出了 MMoE (Multi-gate Mixture-of-Experts) 模型，一种基于“软参数共享”的高效 MTL 架构。MMoE 通过引入门控机制和专家网络，能够显式地建模任务间的关系，并根据输入数据自适应地调整共享策略。本文将从模型背景、核心原理、梯度更新机制及应用价值等方面，对 MMoE 进行全面而深入的解析。

一、 多任务学习的挑战：从硬共享到软共享

1.1 硬共享架构的局限性

在 MMoE 出现之前，最广泛应用的多任务学习架构是 Shared-Bottom 模型，即硬参数共享 。该模型通常由一个共享的底层网络（Shared-Bottom）和多个任务专属的上层网络（Towers）构成 。

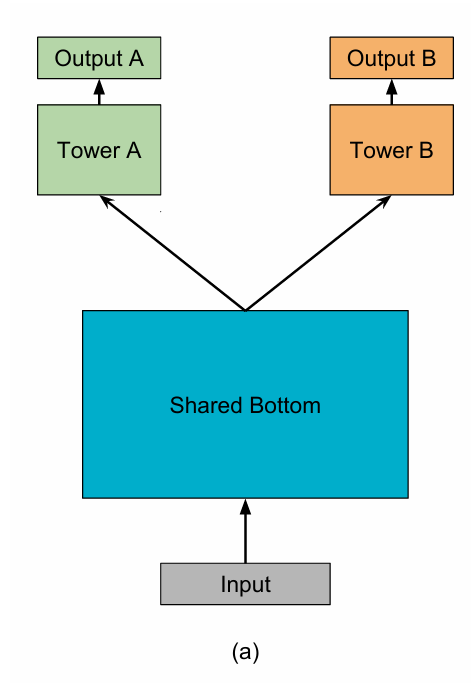
这种架构的优点是结构简单、参数共享率高。然而，其核心缺陷在于“不加区分”的共享机制。当多个任务的目标存在冲突或相关性不高时，共享底层被迫去学习一种能“兼顾”所有任务的中间表示。这会导致优化过程中产生梯度冲突，共享层参数的更新方向相互矛盾，最终损害部分甚至全部任务的性能。实验证明，当任务相关性较低时，Shared-Bottom 模型的性能会显著下降。

1.2 MMoE 的思路演进

为了克服硬共享的局限性，MMoE 提出了一种“软参数共享”（Soft Parameter Sharing）的思路。其设计哲学从“所有任务必须共享同一份知识”的硬约束，演变为“为所有任务提供一个可供选择的、多样化的知识库（专家网络），并让每个任务自主决定如何组合使用这些知识”。这种思路借鉴了经典的 Mixture-of-Experts (MoE) 思想，并将其巧妙地适配到了多任务学习场景中。

二、 MMoE 核心原理与架构

2.1 核心思想概述

MMoE 的核心手段是：通过设置一组共享的专家网络（Experts），并为每个任务配备一个独立的门控网络（Gating Network），让模型能够根据输入数据，为每个任务动态地、自适应地学习出专家的最佳组合权重。

2.2 模型架构拆解

MMoE 的架构主要由三个核心组件构成：

• 专家网络 (Expert Networks)：这是一组结构相同、但参数独立的共享前馈网络。每个专家都可以被视为一个独立的特征提取器，它们从不同角度学习和捕捉输入数据中的信息。所有任务共享这一组专家网络。
• 门控网络 (Gating Networks)：每个任务都拥有一个专属的、通常是轻量级的门控网络（例如一个简单的线性层）。门控网络接收原始输入，其输出经过 Softmax 函数归一化后，生成一组权重，这组权重的维度与专家的数量相同。这组权重决定了各个专家对于当前任务的贡献度。
• 任务塔 (Task Towers)：每个任务拥有一个专属的上层网络，负责处理由门控网络加权融合后的专家信息，并产出符合该任务目标的最终预测值。

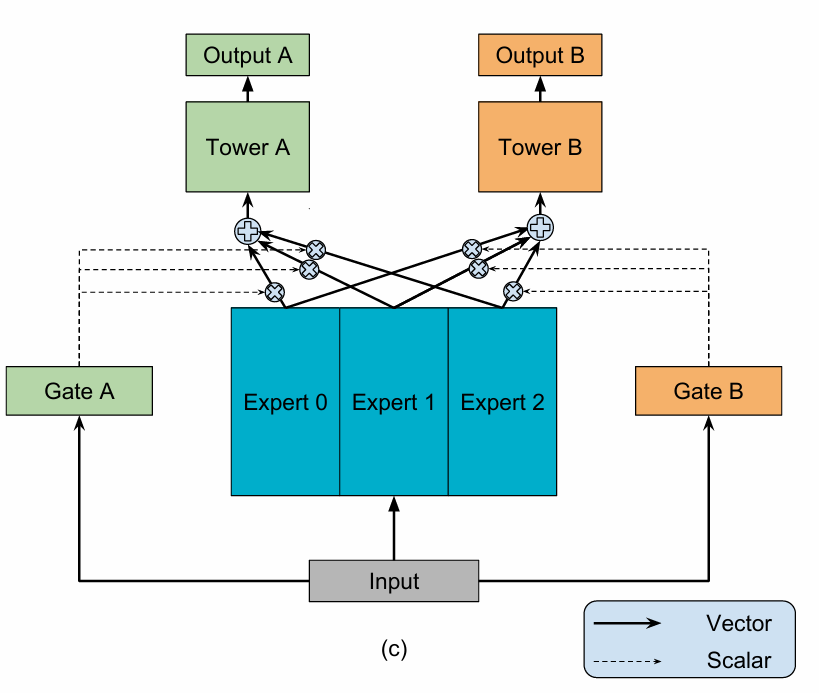
2.3 关键公式解析

假设有 K 个任务，n 个专家。对于第 k 个任务，其输出 y_k 的计算过程可以形式化地表示为：

\[y_k = h^k(f^k(x)) \]

其中，h^k 是第 k 个任务的任务塔，f^k(x) 是经过门控网络加权后的专家输出，其计算方式如下：

\[f^k(x) = \sum_{i=1}^{n} g^k(x)_i f_i(x) \]

这里，f_i(x) 是第 i 个专家网络的输出，g^k(x)_i 是第 k 个门控网络为第 i 个专家生成的权重。门控网络的计算非常简洁：

\[g^k(x) = \text{softmax}(W_{gk}x) \]

其中 W_gk 是第 k 个门控网络的可学习参数矩阵。

三、 梯度更新与参数学习机制

3.1 损失函数

MMoE 的总损失函数通常是各个任务损失的加权和：

\[L_{total} = \sum_{k=1}^{K} w_k L_k(y_k^{true}, y_k^{pred}) \]

其中 L_k 是第 k 个任务的损失函数，w_k 是其对应的权重。

3.2 梯度流向分析

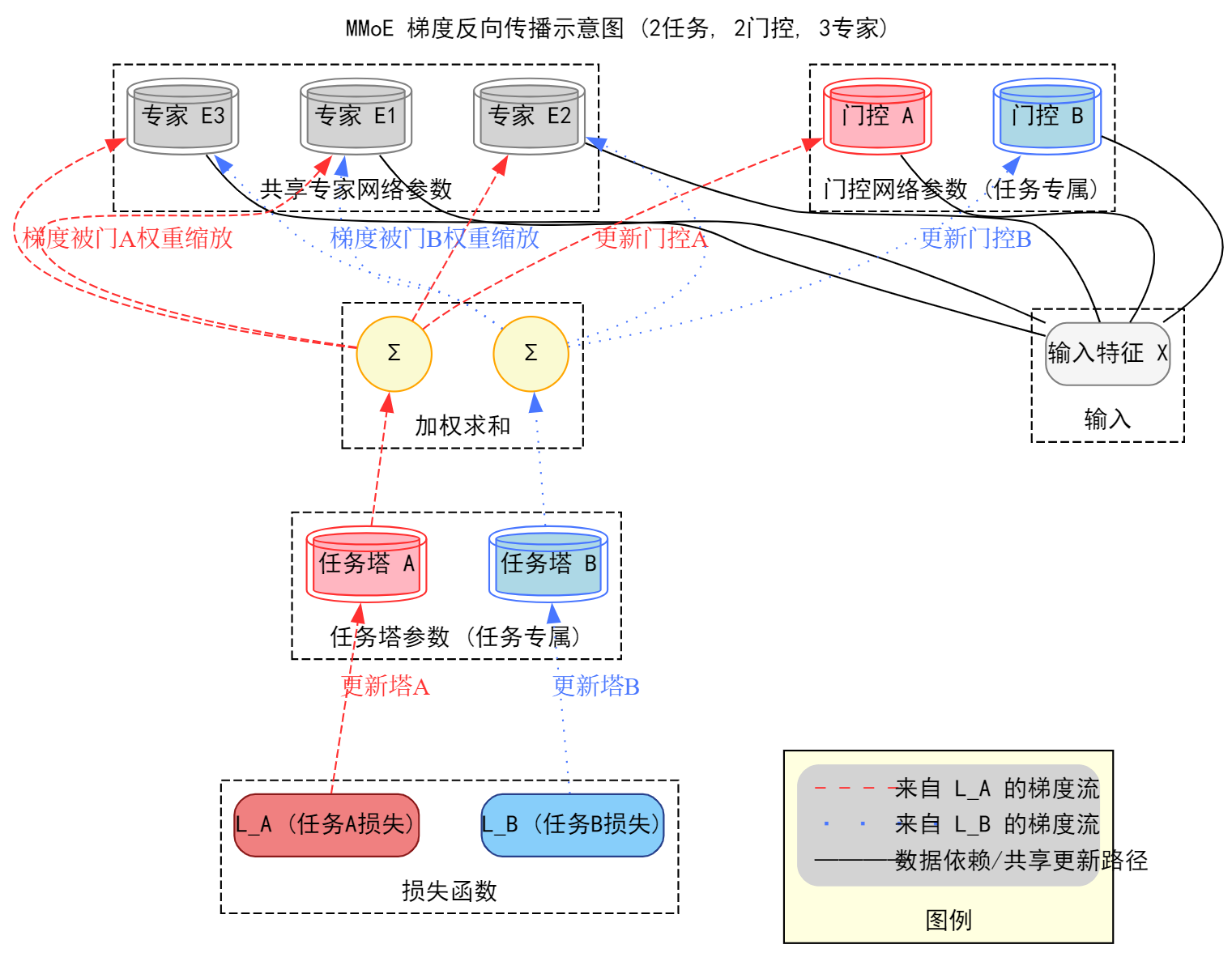
MMoE 的软共享机制在梯度反向传播中体现得淋漓尽致：

• 任务专属部分（塔和门控）：任务 k 的损失 L_k 在反向传播时，其梯度只会流向并更新任务塔 k 和门控网络 k 的参数。这部分参数的更新是任务间完全独立的。
• 共享部分（专家）：所有专家网络的参数会接收来自所有任务的梯度。关键在于，从任务 k 流向专家 i 的梯度大小，在计算上会乘以门控网络 k 为专家 i 生成的权重 g^k(x)_i。这意味着，如果一个任务的门控网络为某个专家分配了较高的权重，那么该任务的损失将在更大程度上影响这个专家的参数更新。

这种机制使得专家网络可以在训练中逐渐特化。一些专家可能因为被某些任务频繁地赋予高权重，而演变为专门服务于这些任务的“领域专家”，而另一些专家则可能学习更为通用的模式。

四、 优缺点与适用场景

4.1 主要优点

• 有效建模任务关系：MMoE 能够根据数据自动学习任务间的关系，在任务相关性不强的场景下，其性能显著优于硬共享模型。
• 提升模型可训练性：论文通过实验发现，MMoE 的门控结构有助于模型在非凸的损失空间中更好地优化，使其相比 Shared-Bottom 模型更不容易陷入差的局部最优，对数据和初始化的随机性更鲁棒。
• 参数效率高：相比于为每个任务构建独立模型或采用复杂的参数共享策略，MMoE 在不显著增加额外参数的情况下，就能有效提升多任务学习的效果。

4.2 潜在局限性

• “跷跷板”现象：在任务间冲突性极强的场景下，由于所有专家网络仍然是全局共享的，它们依然会接收到来自不同任务的冲突梯度。尽管门控机制可以调节梯度的大小，但仍可能出现顾此失彼的“跷跷板”现象（即提升一个任务的性能，却损害了另一个任务的性能）。这个问题由其后续的演进模型 PLE 进一步针对性解决。
• 引入新超参：专家数量（num_experts）成为一个需要细致调节的关键超参数。专家过少可能无法捕捉任务间的多样性，过多则可能导致训练困难和过拟合。

4.3 适用场景

MMoE 极其适用于具有多个优化目标，且任务间关系未知或复杂的工业级应用。

• 大规模推荐系统：例如，在视频或新闻推荐中，系统需要同时优化点击率、完播率、点赞率、分享率等多个目标。
• 各类多任务学习问题：任何希望通过一个统一模型解决多个相关联任务，并期望模型能自动学习任务间共享模式的场景。

五、 代码实现

import torch
import torch.nn as nn
import torch.nn.functional as Fclass MMoE(nn.Module):"""MMoE: Multi-gate Mixture-of-Experts PyTorch Implementation.该类实现了MMoE模型，论文详见:"Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts"by Ma et al.核心思想 Core Ideas:1.  **专家混合网络 (Mixture-of-Experts)**: 模型包含多个并行的"专家"子网络，它们都是共享的，可以学习通用的底层特征表示2.  **多门控机制 (Multi-gate)**: 每一个学习任务都有一个独立的"门控网络"。这个门控网络会根据输入动态地生成一组权重，用于对所有专家的输出进行加权求和3.  **软共享 (Soft Sharing)**: 通过这种方式，每个任务都能学到一种最适合自己的专家组合方式，实现了参数的软共享，相比硬共享更加灵活，能有效缓解任务间的负迁移现象Args:input_dim (int): 输入特征的维度。num_tasks (int): 任务的数量。num_experts (int): 专家网络的数量。expert_hidden_dims (list): 定义每个专家网络隐藏层维度和结构的列表。tower_hidden_dims (list): 定义每个任务塔隐藏层维度和结构的列表。"""def __init__(self, input_dim, num_tasks, num_experts, expert_hidden_dims, tower_hidden_dims):super(MMoE, self).__init__()# --- 核心模块定义 ---self.input_dim = input_dimself.num_tasks = num_tasksself.num_experts = num_experts# --- 模块一: 专家网络 (Expert Networks) ---# 专家网络是共享的，所有任务都可以利用它们。# 使用 nn.ModuleList 来存储所有的专家网络。self.experts = nn.ModuleList([self._build_mlp(self.input_dim, expert_hidden_dims) for _ in range(self.num_experts)])# --- 模块二: 门控网络 (Gating Networks) ---# 每个任务一个门控网络，用于学习专家的权重。# 每个门控网络是一个简单的线性层，输出维度等于专家的数量。self.gates = nn.ModuleList([nn.Linear(self.input_dim, self.num_experts) for _ in range(self.num_tasks)])# --- 模块三: 任务塔 (Task-specific Towers) ---# 每个任务独有的网络，负责处理加权后的专家输出，并给出最终预测。# 任务塔的输入维度等于专家网络的输出维度。expert_output_dim = expert_hidden_dims[-1] if expert_hidden_dims else self.input_dimself.towers = nn.ModuleList([self._build_mlp(expert_output_dim, tower_hidden_dims) for _ in range(self.num_tasks)])def _build_mlp(self, input_dim, hidden_dims):"""一个辅助函数，用于构建MLP网络（专家网络或任务塔）。"""layers = []for hidden_dim in hidden_dims:layers.append(nn.Linear(input_dim, hidden_dim))layers.append(nn.ReLU())input_dim = hidden_dimreturn nn.Sequential(*layers)def forward(self, x):"""MMoE的前向传播逻辑。Args:x (torch.Tensor): 输入的特征张量，形状为 (batch_size, input_dim)。Returns:list: 包含每个任务最终输出logit的列表。"""# --- 流程 1: 获取所有专家的输出 ---# 将输入x分别送入每个专家网络。expert_outputs = [expert(x) for expert in self.experts]# 将输出堆叠起来，方便后续加权。形状变为 (batch_size, num_experts, expert_output_dim)expert_outputs_stacked = torch.stack(expert_outputs, dim=1)# --- 流程 2: 获取每个任务的门控权重 ---# 将输入x送入每个门控网络，并通过Softmax得到归一化的权重。gate_outputs = [F.softmax(gate(x), dim=1) for gate in self.gates]# --- 流程 3: 任务塔计算 ---task_outputs = []for i in range(self.num_tasks):# 获取当前任务的门控权重# 形状: (batch_size, num_experts)current_gate_weights = gate_outputs[i]# 使用unsqueeze在最后增加一个维度，使其形状变为 (batch_size, num_experts, 1)# 以便与 expert_outputs_stacked (batch_size, num_experts, expert_output_dim) 进行广播乘法weighted_experts = expert_outputs_stacked * current_gate_weights.unsqueeze(-1)# 沿专家维度求和，得到当前任务的融合特征表示# 形状: (batch_size, expert_output_dim)task_specific_input = torch.sum(weighted_experts, dim=1)# 将融合后的特征送入对应的任务塔tower_output = self.towers[i](task_specific_input)task_outputs.append(tower_output)return task_outputs

总结

MMoE 通过借鉴 Mixture-of-Experts 思想，巧妙地设计了“共享专家+独立门控”的软参数共享架构，为多任务学习领域提供了一种优雅且高效的解决方案。它不仅在理论上能够显式地建模任务关系，也在实践中被证明能够有效提升模型性能和可训练性，已成为工业界多任务学习的基石模型之一，并为后续如 PLE 等更先进的 MTL 架构提供了重要的设计思路。