前置算法
- 动态规划
- hash哈希
题目大意
给定一个字符串,可以将相邻两个相同的字符删除,然后合并成一个新序列。
例如:abba,可以先将两个 b 删除,然后合并成 aa,最后删除 a。
求出有多少个字串,最后可以将其变为空串,我们称之为合法的字串。
思路
看到数据范围,只能使用 \(O(n)\) 及以下的时间复杂度来解决这道问题。
思考他的性质,显然如果 [a, b] 和 [b + 1, c] 是一个合法的字串,则 [a, c]。
求解 f[] 数组
考虑动态规划,设 \(f[i]\) 表示以第 \(i\) 个字符为结尾的合法字串有多少个,则 \(f[i] = f[x-1] + 1\),其中 \(x\) 为最大的一个合法区间的左端点。
求解 x[] 数组
可以看到,\(s[x]\) 一定等于 \(s[i]\),并且 [x + 1, i - 1] 一定也是一个合法字串,从而得到 \(x[i] = x[i-1] - 1\),直到 \(s[x[i]] = s[i]\),找不到则等于 \(i\)。
优化
可以发现求解 x[] 的过程比较慢,考虑下面一张图,是求解 x[] 的过程图
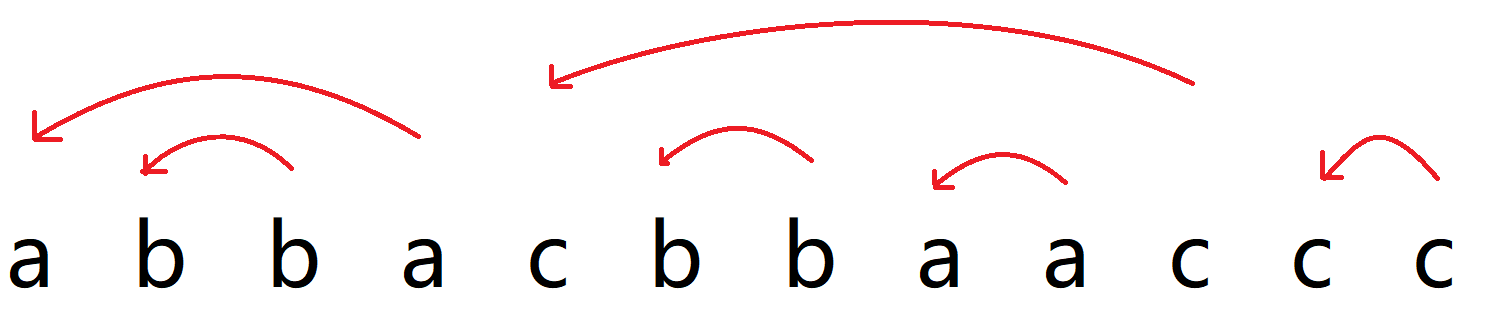
因为每次 x[i] 总是回调到 x[i-1] - 1,所以令 t[i-1] = x[i-1] - 1,则每次 x[i] 只要跳到 t[i-1] 即可
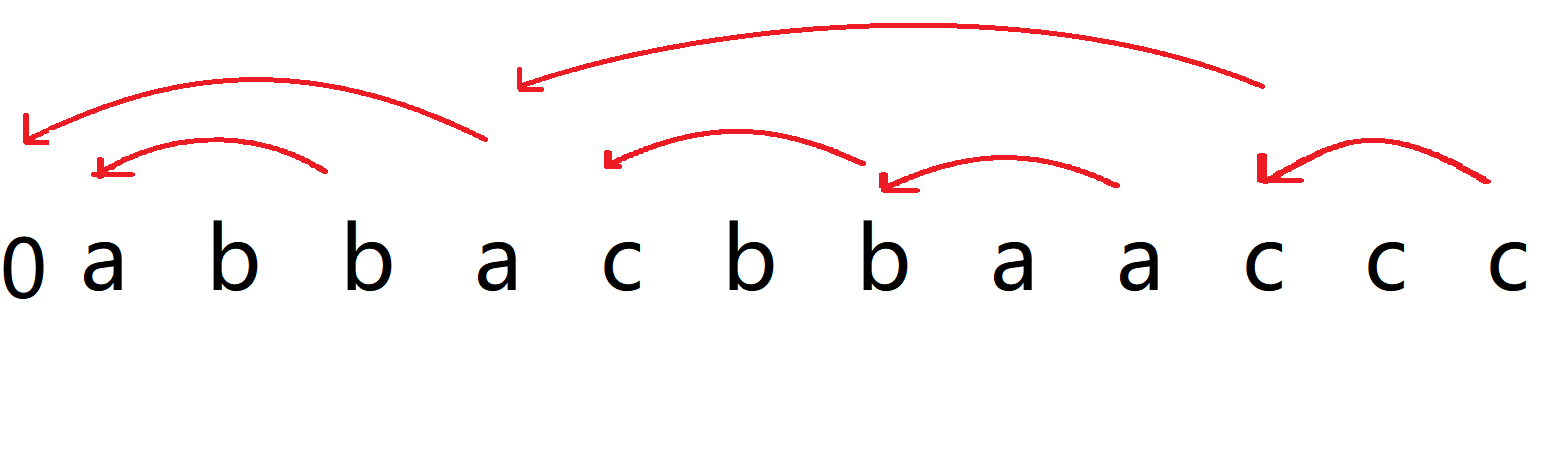
现在可以将他看成几条链,每一条链的编号为链头,用 \(to[i]\) 表示 \(i\) 所在的链的编号即对头是多少,用 \(a[id][c]\) 表示链编号为 \(id\) 的链上,最近的一个字符 \(c\) 的位置,没有则为 \(0\)。
这样就可以在 \(O(n)\) 的时间复杂度内解决这道题。
代码
#include <iostream>
using namespace std;const int N = 2000010;
long long n, dp[N], to[N], a[N][40];
string s;int main() {cin >> n >> s;s = " " + s;for (int i = 1; i <= n; i++) {to[i] = i; // 将链头赋值为 iint x = a[to[i-1]][s[i] - 'a' + 1]; // 找到最近的一个合法左端点if (x) to[i] = to[x-1], dp[i] = dp[x-1] + 1; // 更新dp值a[to[i]][s[i] - 'a' + 1] = i; // 更新 a 数组}long long ans = 0; // 不开 long long 见祖宗for (int i = 1; i <= n; i++)ans += dp[i];cout << ans << endl;return 0;
}
完结撒花!!!


![AT_agc058_b [AGC058B] Adjacent Chmax](http://pic.xiahunao.cn/AT_agc058_b [AGC058B] Adjacent Chmax)

)







)


![[系统] Windows 已有office版本和visio不兼容的解决方案](http://pic.xiahunao.cn/[系统] Windows 已有office版本和visio不兼容的解决方案)

![AT_agc055_b [AGC055B] ABC Supremacy](http://pic.xiahunao.cn/AT_agc055_b [AGC055B] ABC Supremacy)

