[python 刷题] 84 Largest Rectangle in Histogram

题目：

Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

这题也是一个典型的 monotonic stack 的题，解题思路是将 (x, y) 的配对保存到 stack 中，其中 x 为当前 histogram 可能达到的最左侧点，即最大长度，而 y 则是保存当前 histogram 最大高度。其逻辑是，对于 histogram 来说，随着 x 轴增长时，会遇到以下三种情况：

• y 出现增加

  

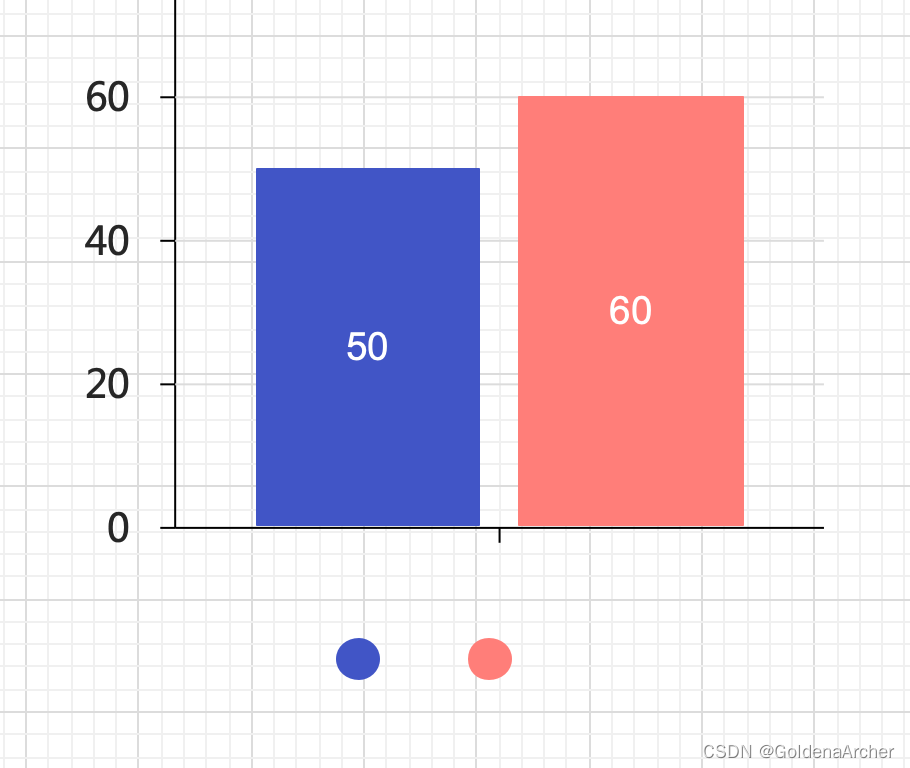
  当前情况下，蓝色方块 y 不受限制，x 是可以继续延伸的，此时可以将对应的 x 和 y 存到 stack 中，stack 中的值为 [(0, 50)]：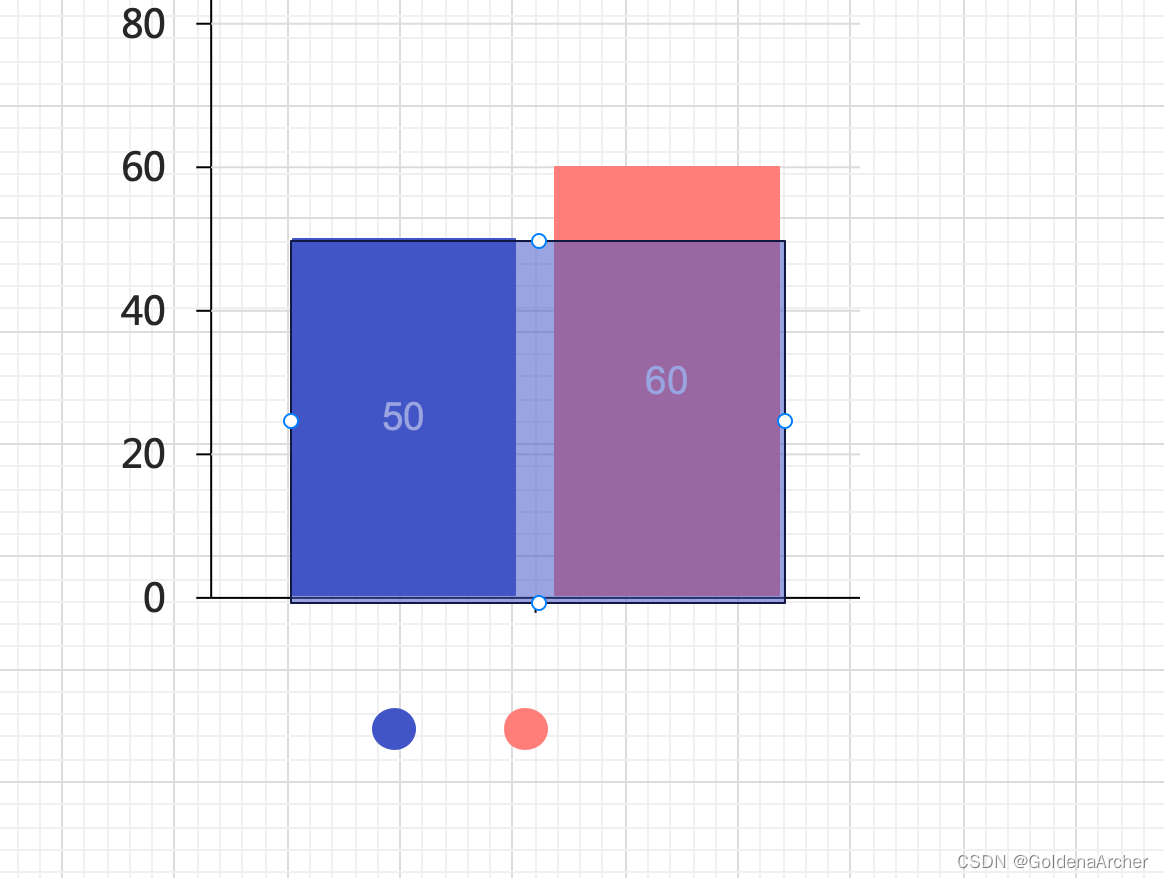

  

• y 出现减少

  

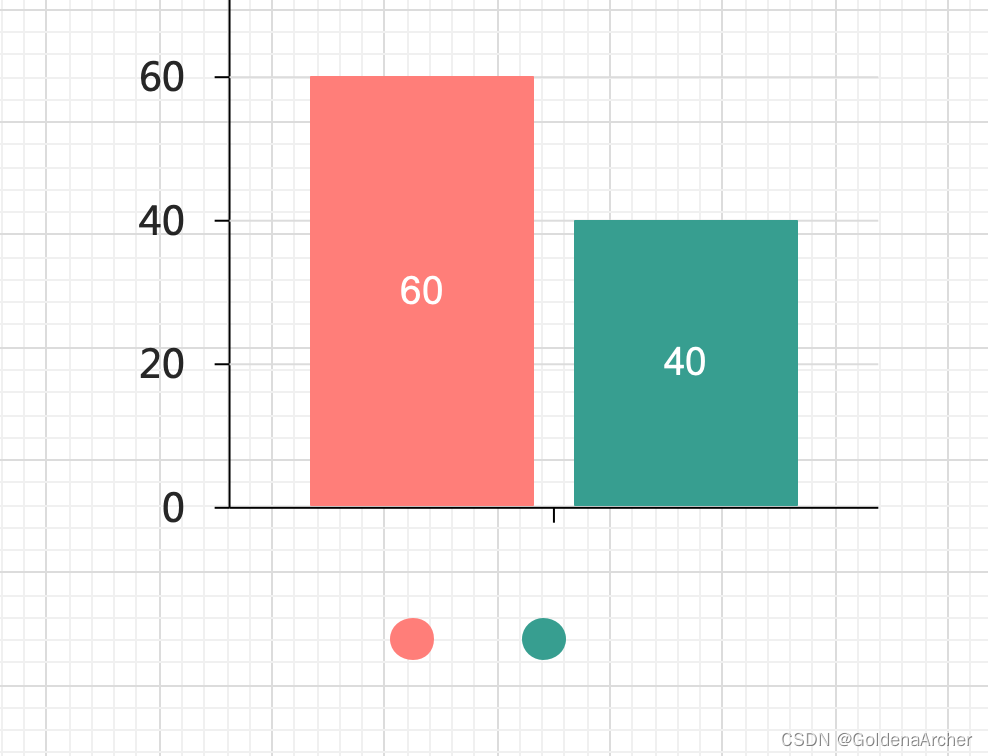
  当前情况下，粉色方块的 y 轴受到限制，x 是不可延续的：

  

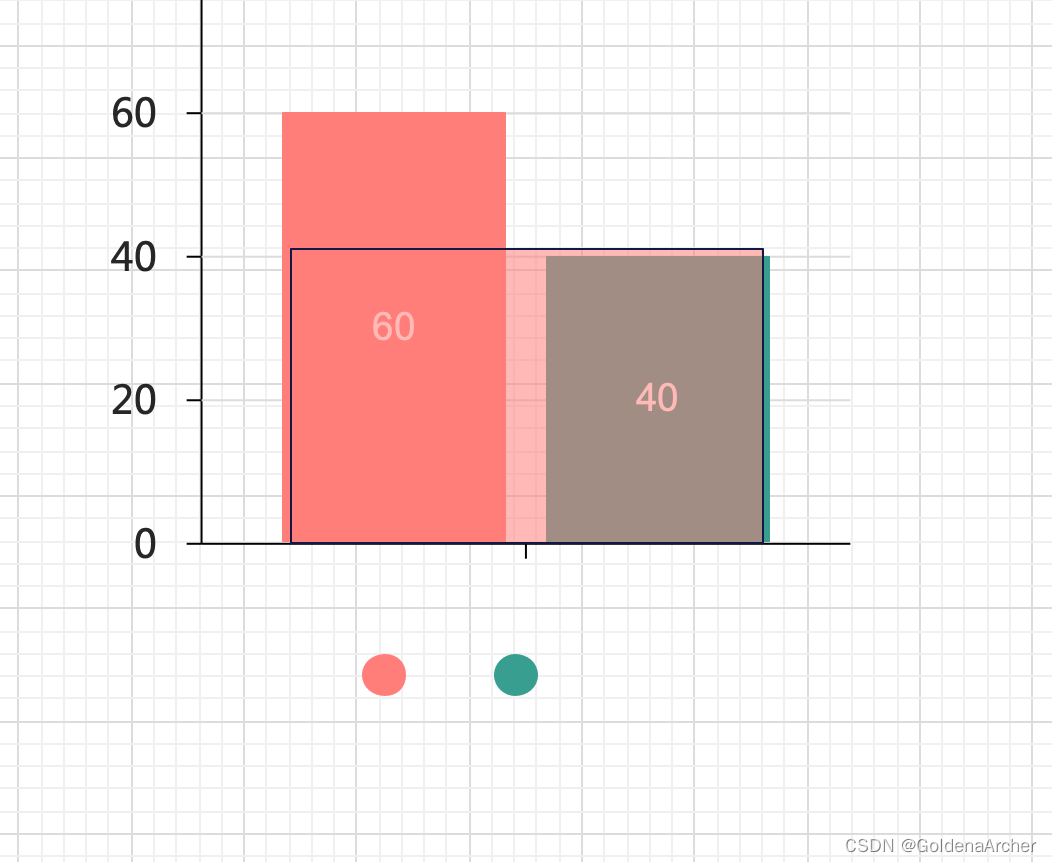
  因此就需要进行一个退栈的操作，计算粉色 histogram 的最大面积

• y 保持不变

  这个情况可以单独处理，不过默认作为 y 出现增加 情况处理也行

继续过一遍官方提供的案例加深理解：heights = [2,1,5,6,2,3]

当遍历到第一个值时，stack 为空，没有什么可以进行对比的，因此进行一个入栈的操作：

当遍历到第二个值 1 时，stack[-1] 的高度无法延伸到当前值，因此进行一个退栈计算面积、对比最大面积、将新的值压入栈中的操作

注意，这里 🟩 沿用了 🟥 的下标，因为 🟥 的 x 无法延伸到 🟩 ，但是 🟩 的 x 可以反向延伸到 🟥 上：

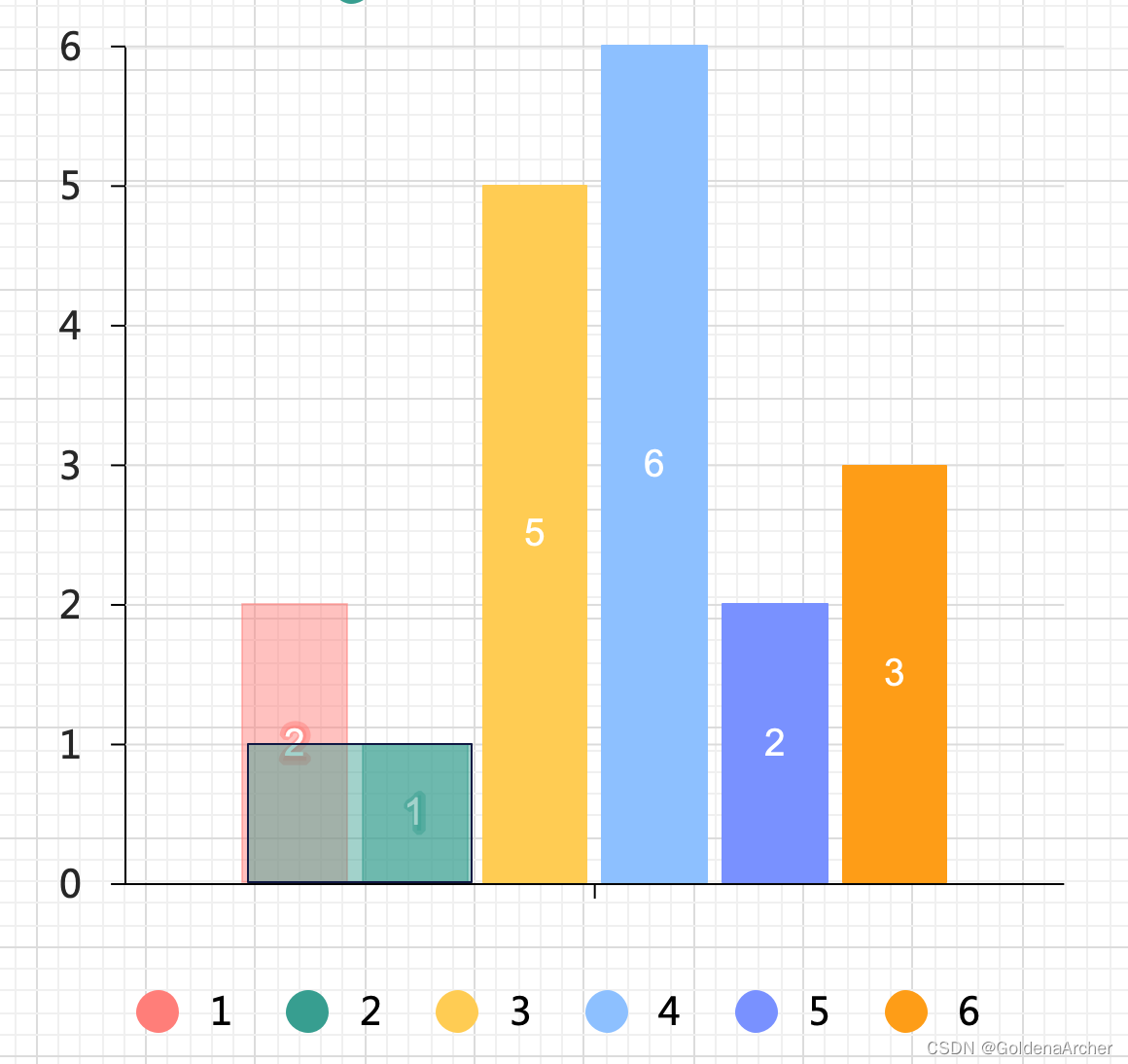
所以每次出栈的时候都要获取 stack[-1].x 的值，以供让下一个矮一点的 histogram 去继承

遍历到第三个值 5 时，stack[-1] 可以延伸到下一个 histogram 上，因此只是进行一个入栈的操作：

遍历到第四个值 6 时，stack[-1] 可以延伸到下一个 histogram 上，因此只是进行一个入栈的操作：

这两个操作一样，因此合并成一张图

当遍历到 2 的时候，再次遇到 y 轴不可眼神的情况，因此要进行连续退栈的操作，因为 stack 中倒数两个值都比当前遇到的 histogram 要大。其面积的计算方式都为 $(currX-stack[-1].x)\times y$

• 对于 6 来说，其面积为 $(4-3)\times 6$
• 对于 5 来说，其面积为 $(4-2)\times 5$
• 对于 1 来说，它的 y 轴依然可延续，因此不会进行退栈的操作

此时栈的值如下：

⚠️：上面提到了矮的 histogram 其实是可以反向延长的，因此这里 🟪 占用的是 🟨 的下标

之后重复遍历，一直到完成数组遍历，不过此时 stack 中还是有多余的值的，这个情况下代表 stack 中的 histogram，其 x 轴可以一直延伸到最右端，因此可以用 len(heights) - stack[-1].x 的方法获取其对应的 x，再乘以对应的 y，获得最终面积

代码如下：

class Solution:def largestRectangleArea(self, heights: List[int]) -> int:stack = []max_area = 0for i, h in enumerate(heights):start = iwhile stack and stack[-1][1] > h:prev_i, prev_h = stack.pop()max_area = max(max_area, prev_h * (i - prev_i))start = prev_i# 反向延长 x 轴stack.append((start, h))for i, h in stack:max_area = max(max_area, h * (len(heights) - i))return max_area