Day11 when gradient is small……
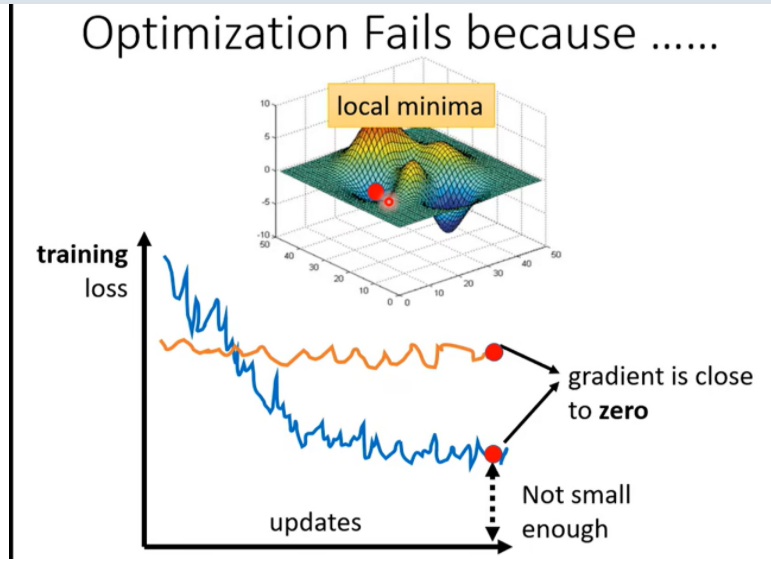


怎么知道是局部小 还是鞍点?
using Math

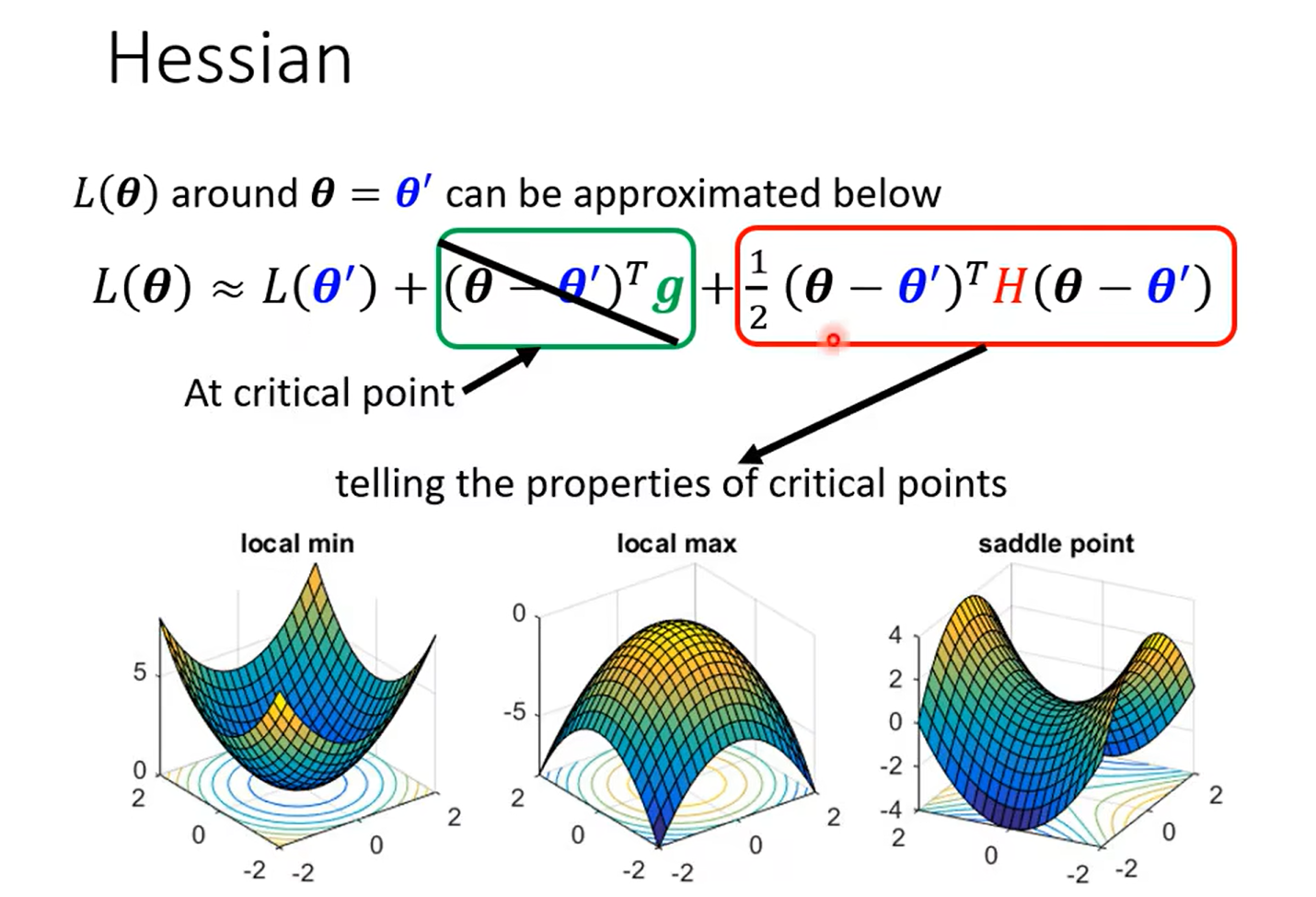
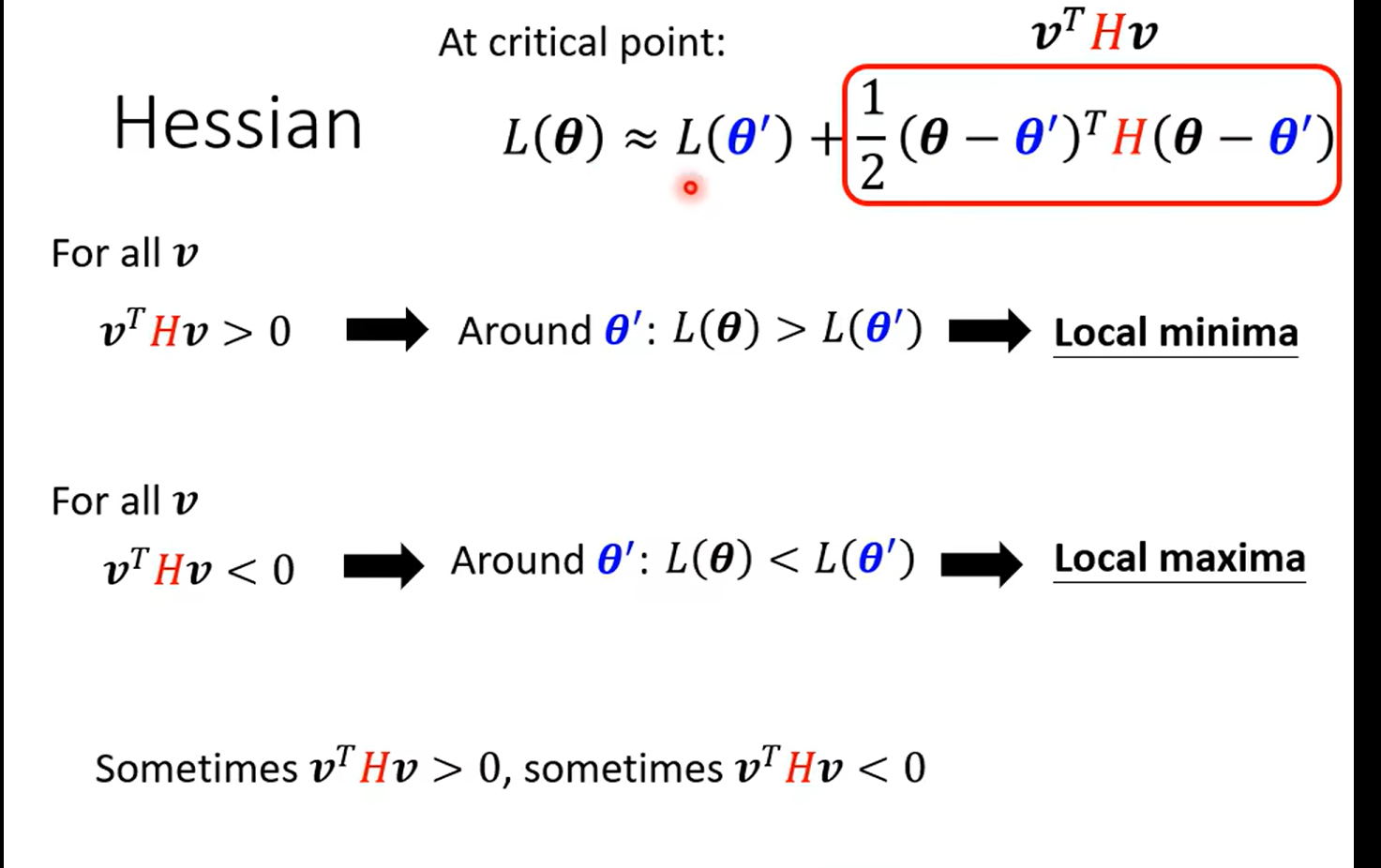
这里巧妙的说明了hessan矩阵可以决定一个二次函数的凹凸性 也就是 θ \theta θ 是min 还是max,最后那个有些有些 哈 是一个saddle;
然后这里只要看hessan矩阵是不是正定的就好(详见 线性代数)
example – using Hessan
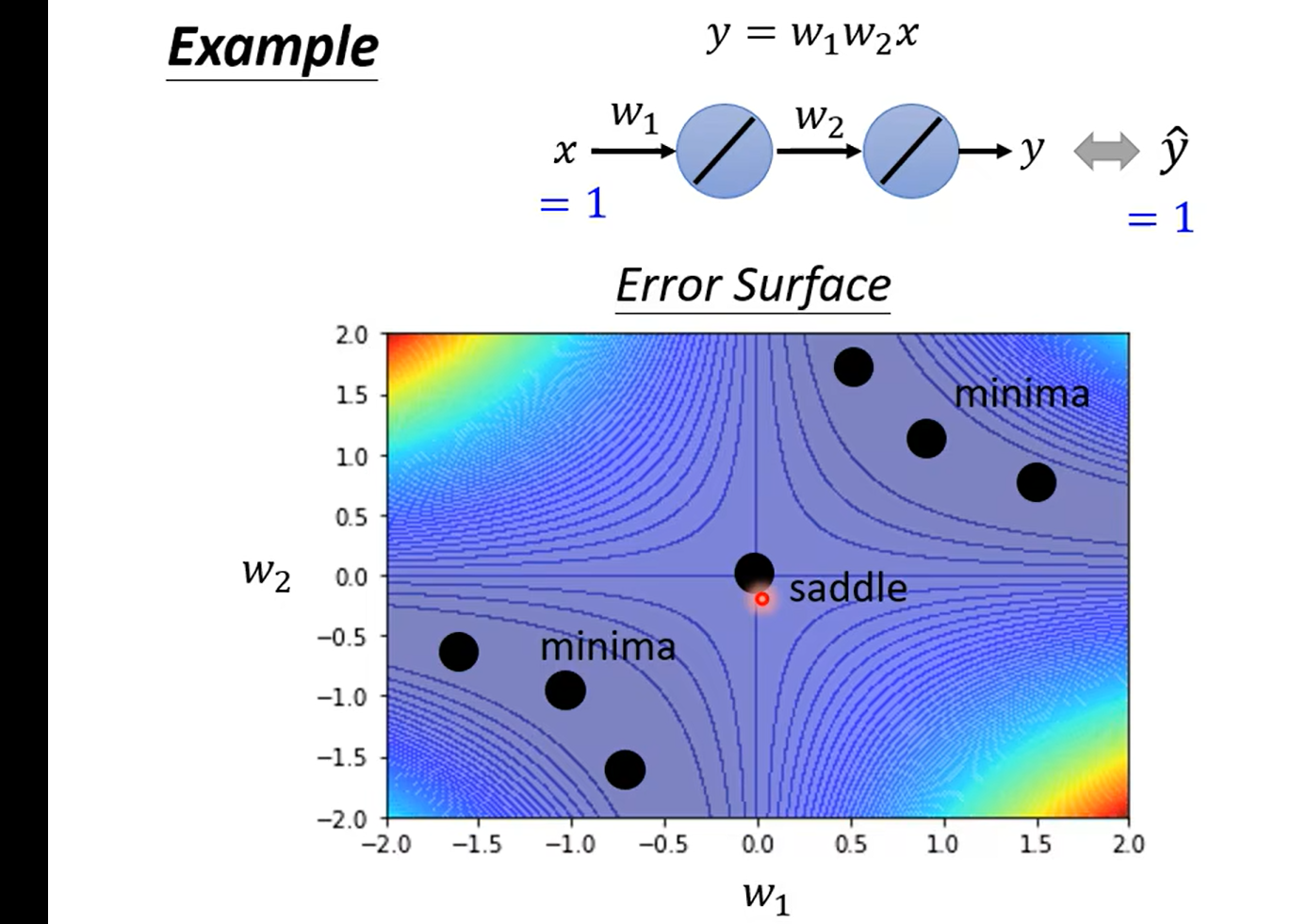
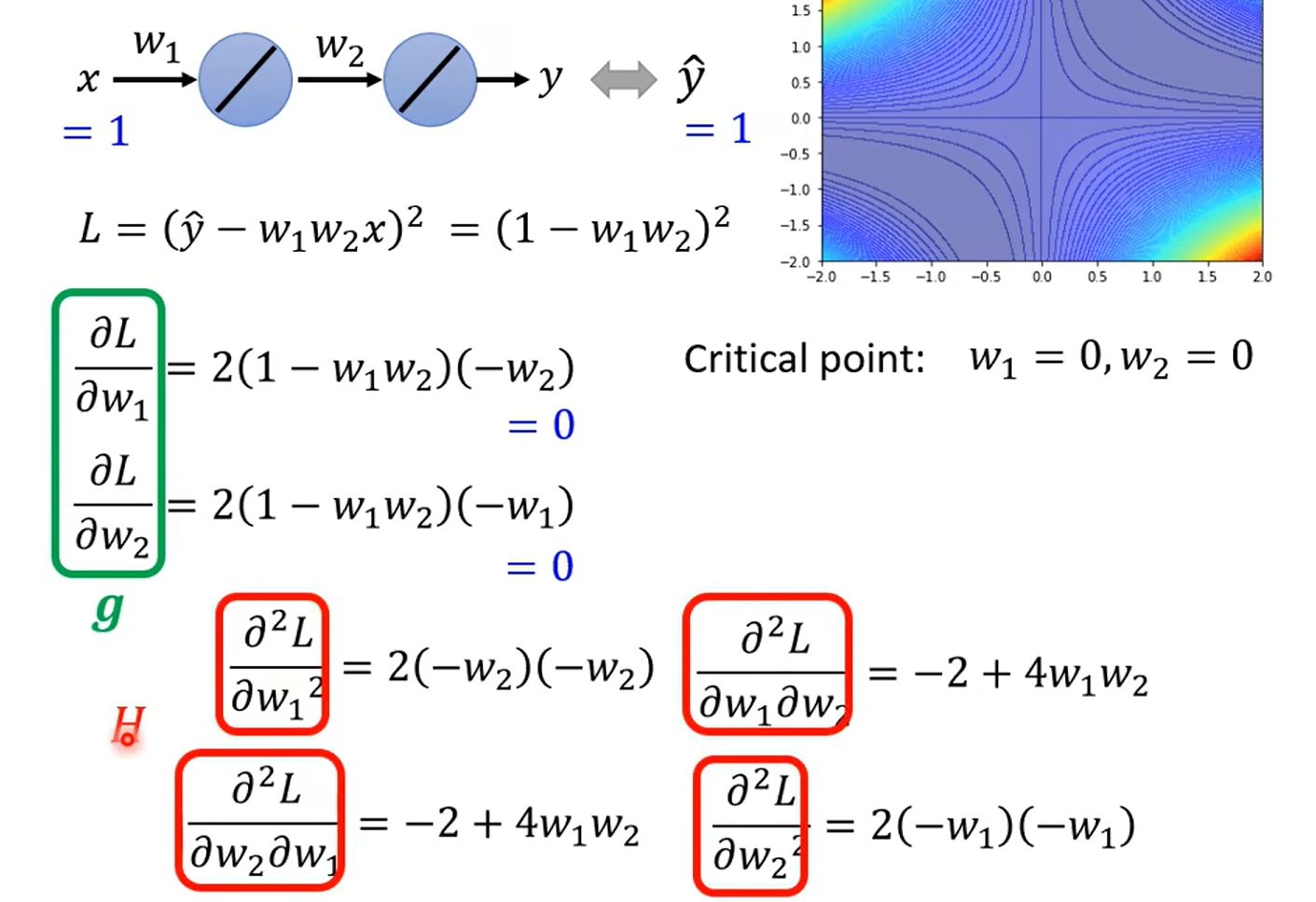
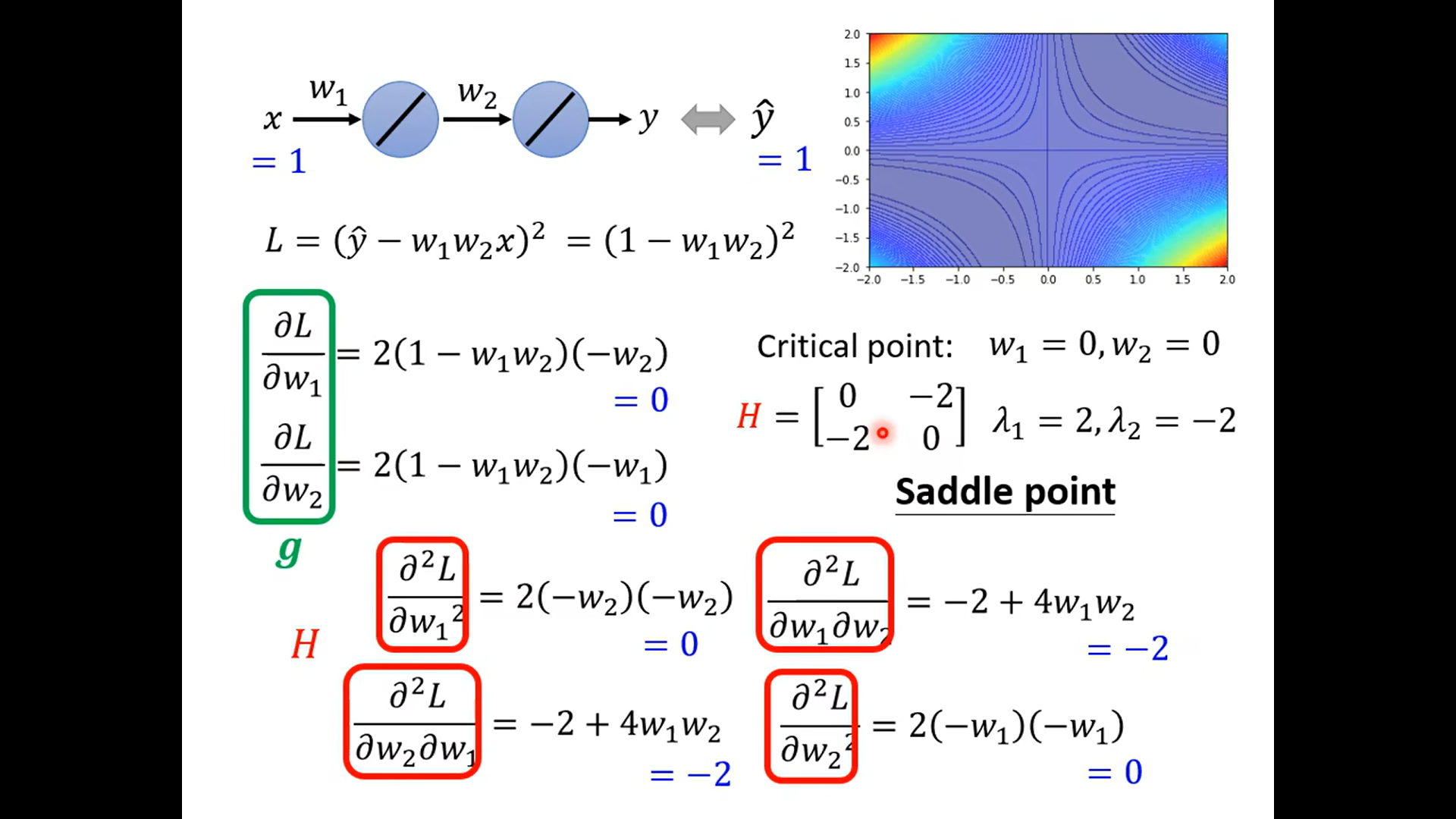
奇怪这里为什么不是主对角线呀,难道两个都一样嘛 晕死,得复习线代了
Dont afraid of saddle point(鞍点)

征向量 u 和对应的特征值 λ定义为满足下列关系的向量和标量:Hu=λu
在梯度下降算法中,我们希望选择使得 L*(*θ) 减小的 θ 方向。如果 λ<0,则向 u 的方向移动参数 θ 会减小损失函数 L(θ)。
换句话说,如果我们发现了一个负特征值λ 和相应的特征向量u,我们可以通过沿着 u 的方向更新 θ 来降低损失函数的值。这就是图中所说的“Decrease L”的含义。

local minima VS saddle Point
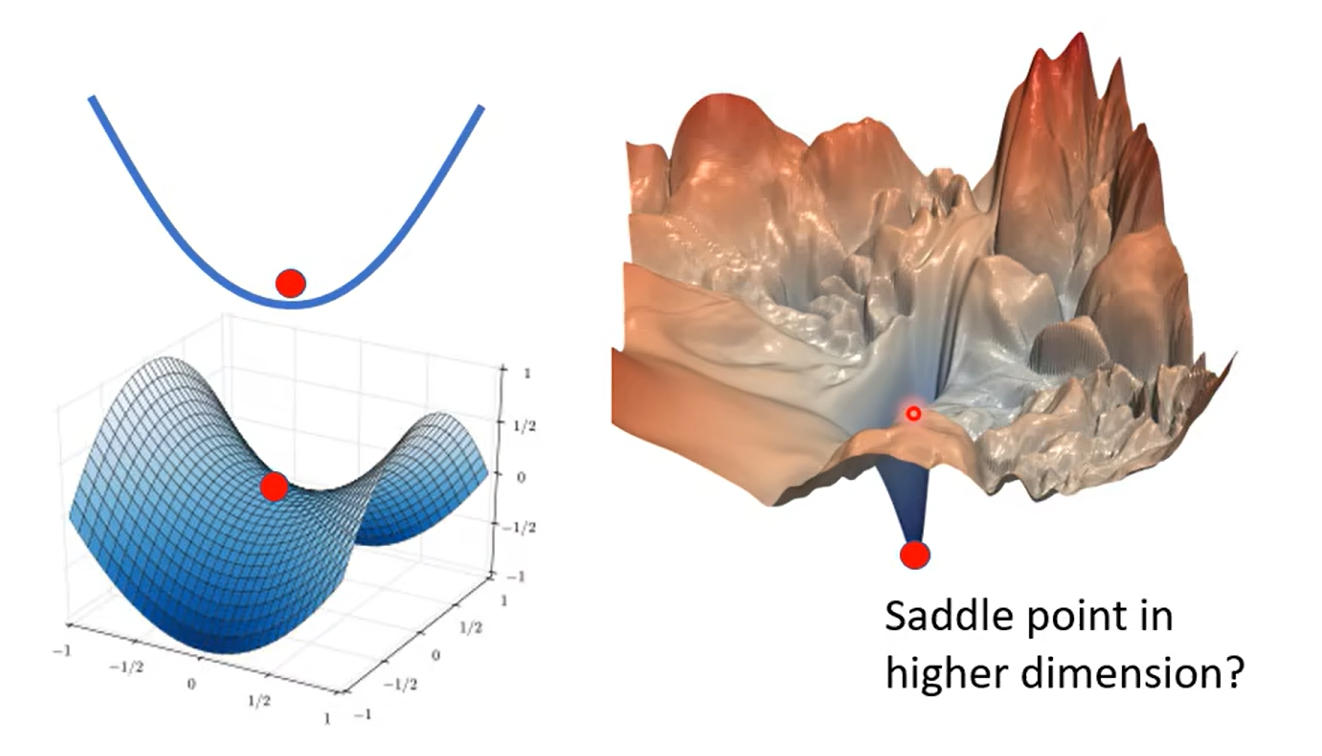

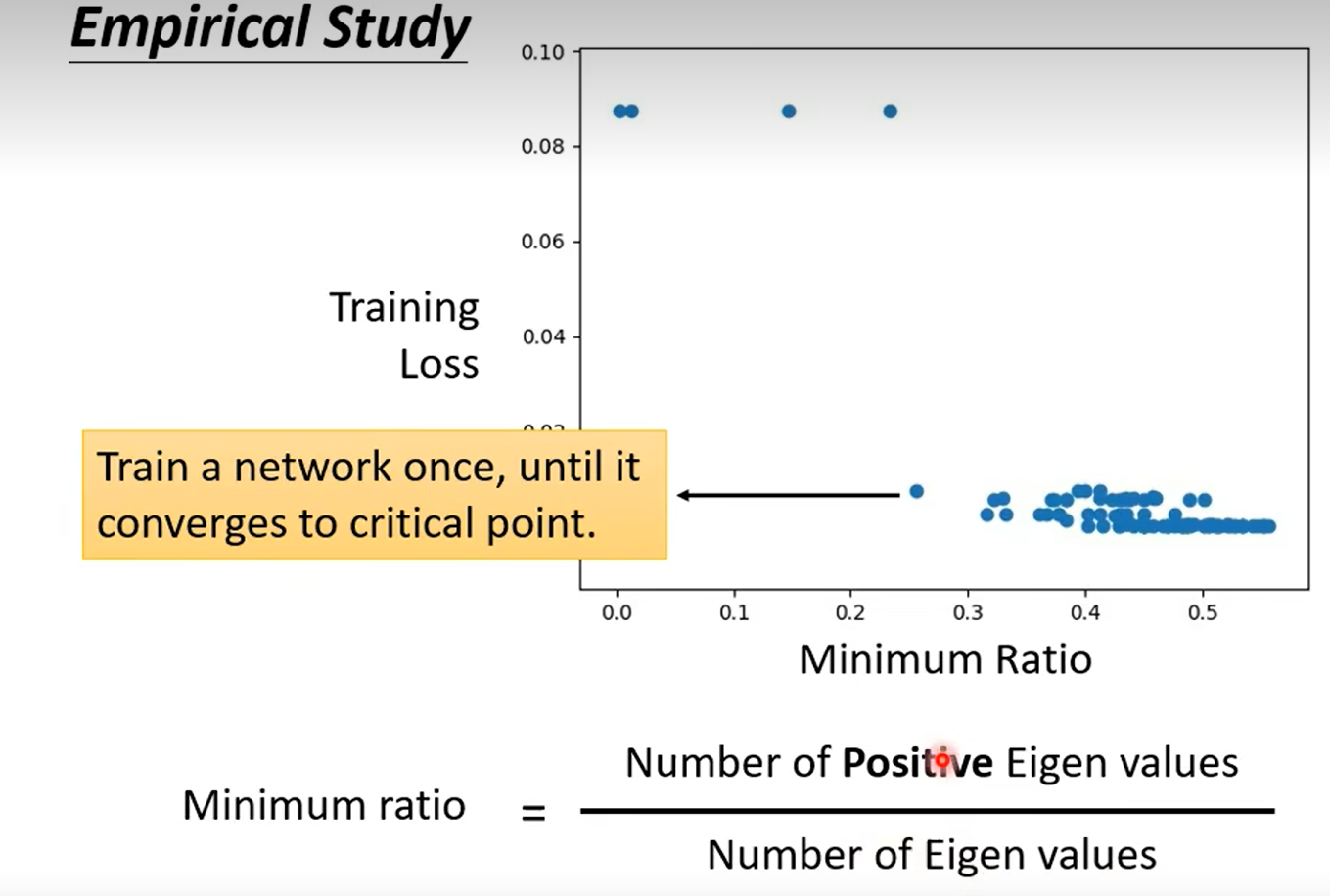
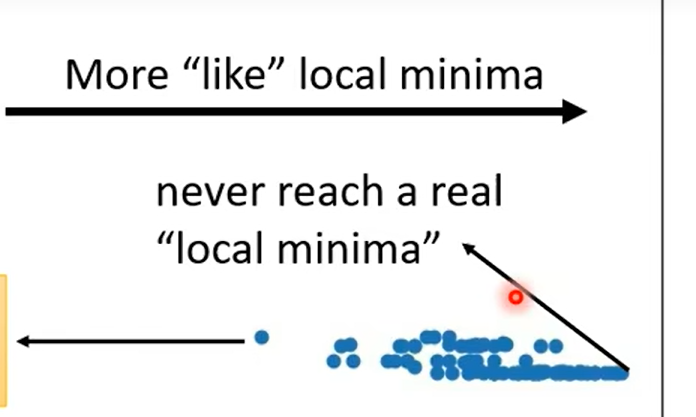
引入高维空间的观点,解决local minima的问题:我们很少遇到local minima;
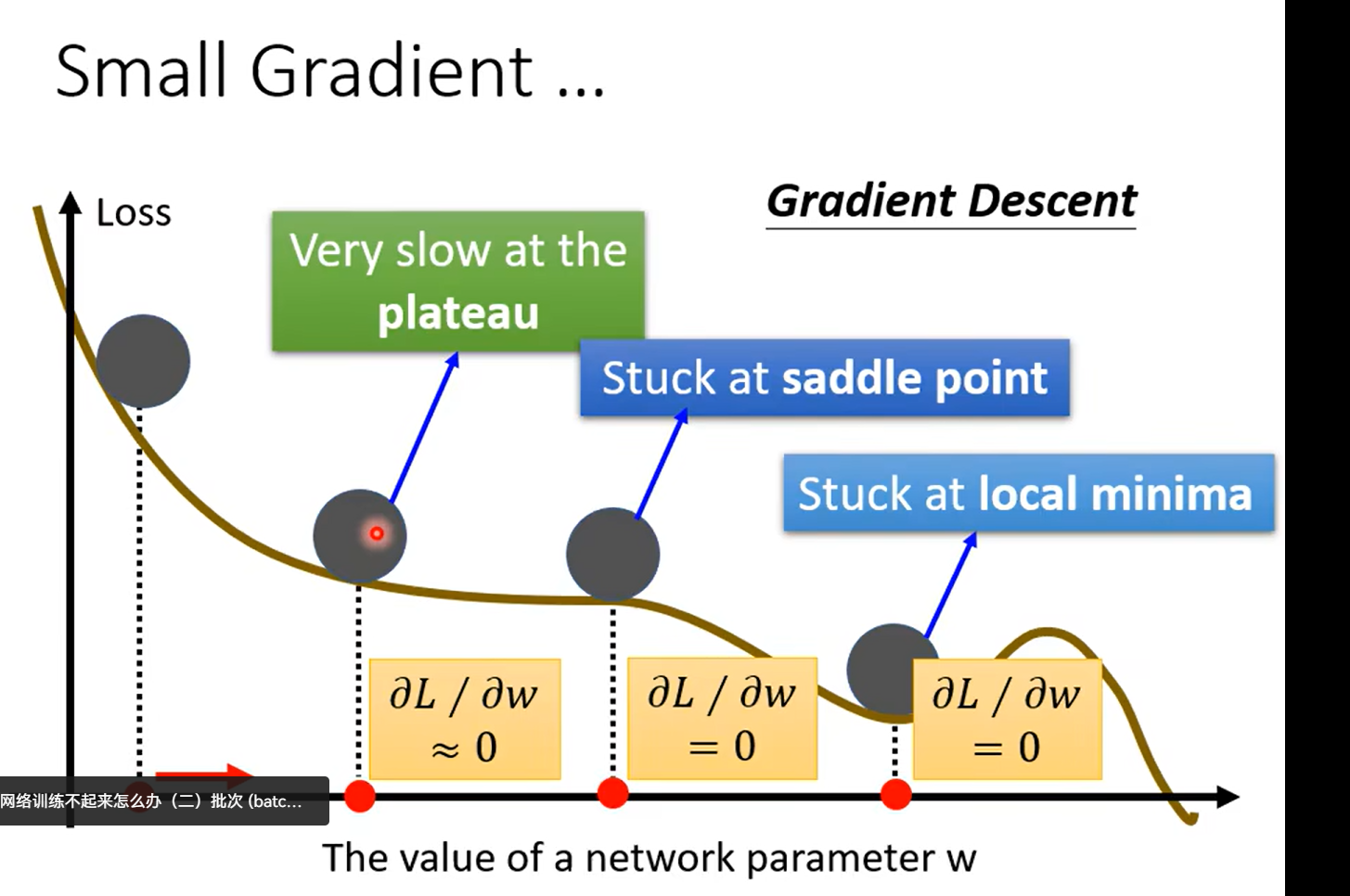
Day12 Tips for training :Batch and Momentum
why we use batch?
前面有讲到这里, 前倾回归
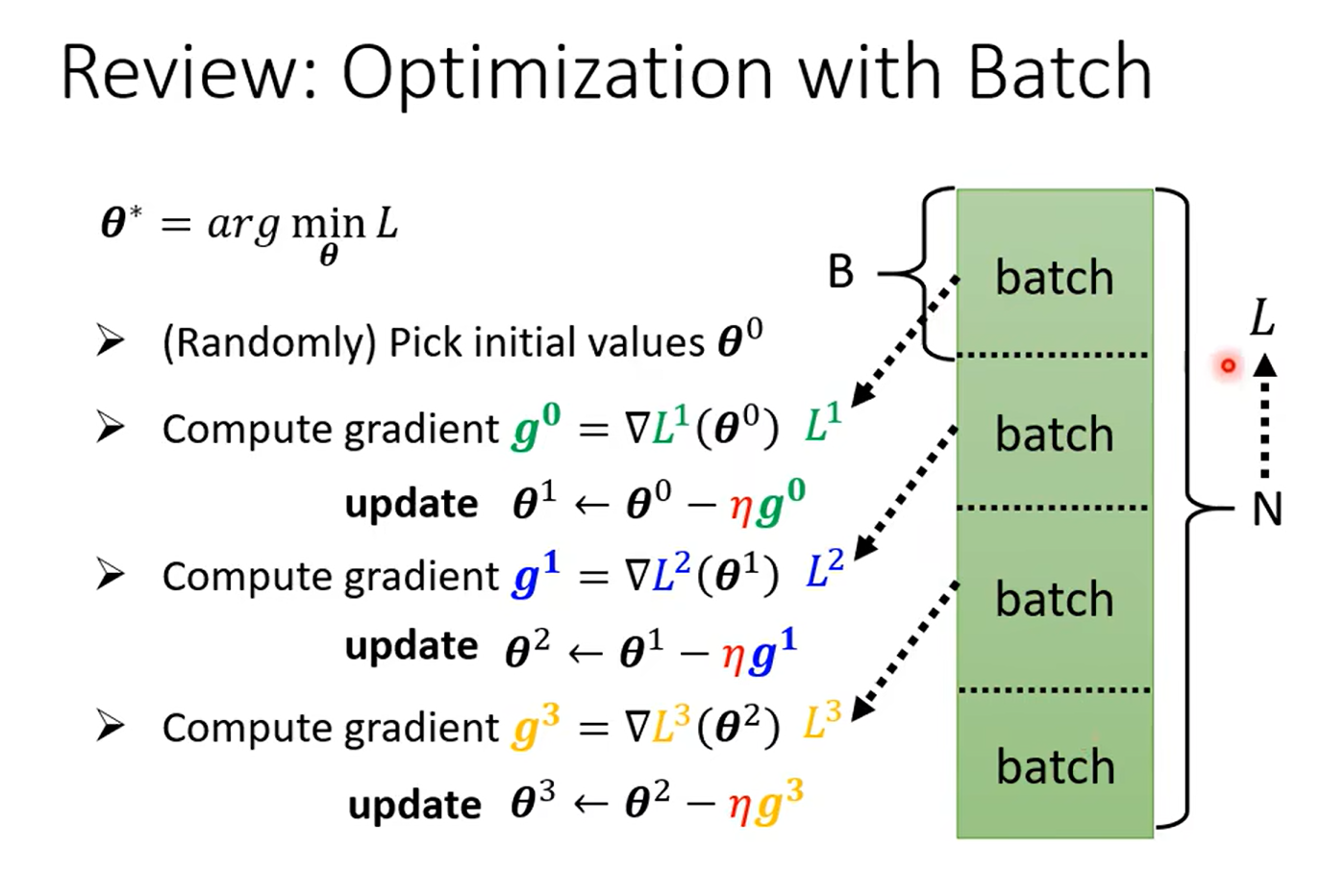

这里大家记得问自己一个问题:一个epoch 更新多少个参数?nums(batch)* parameters
例如,如果你有100个batch,那么在完成一个epoch后,每个参数会被更新100次。
shuffle :有可能batch结束后,就会重新分一次batch
small vs big
这里举了两个极端的例子,也是我们常见的学习方法:取极限看效果
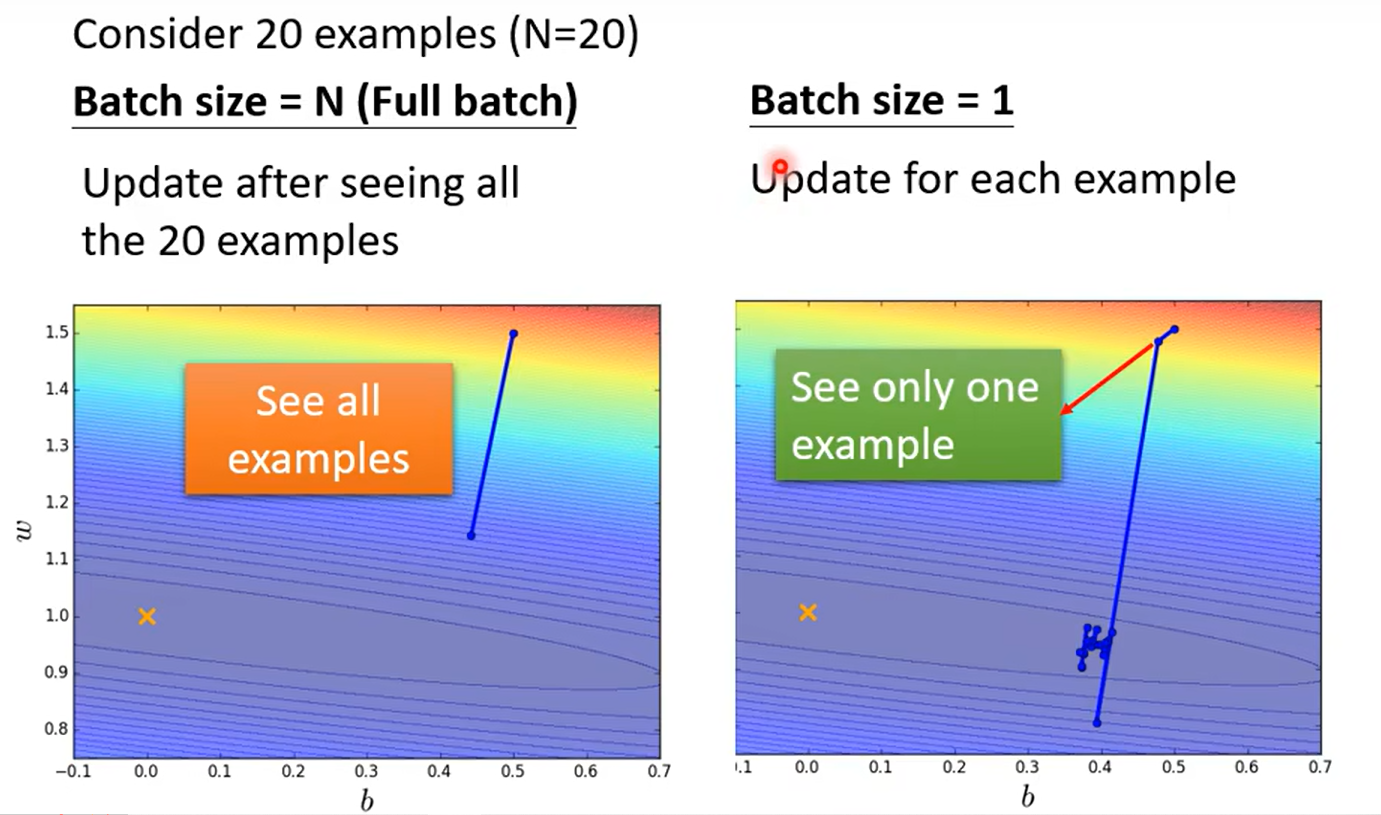

未考虑平行运算(并行 --gpu)
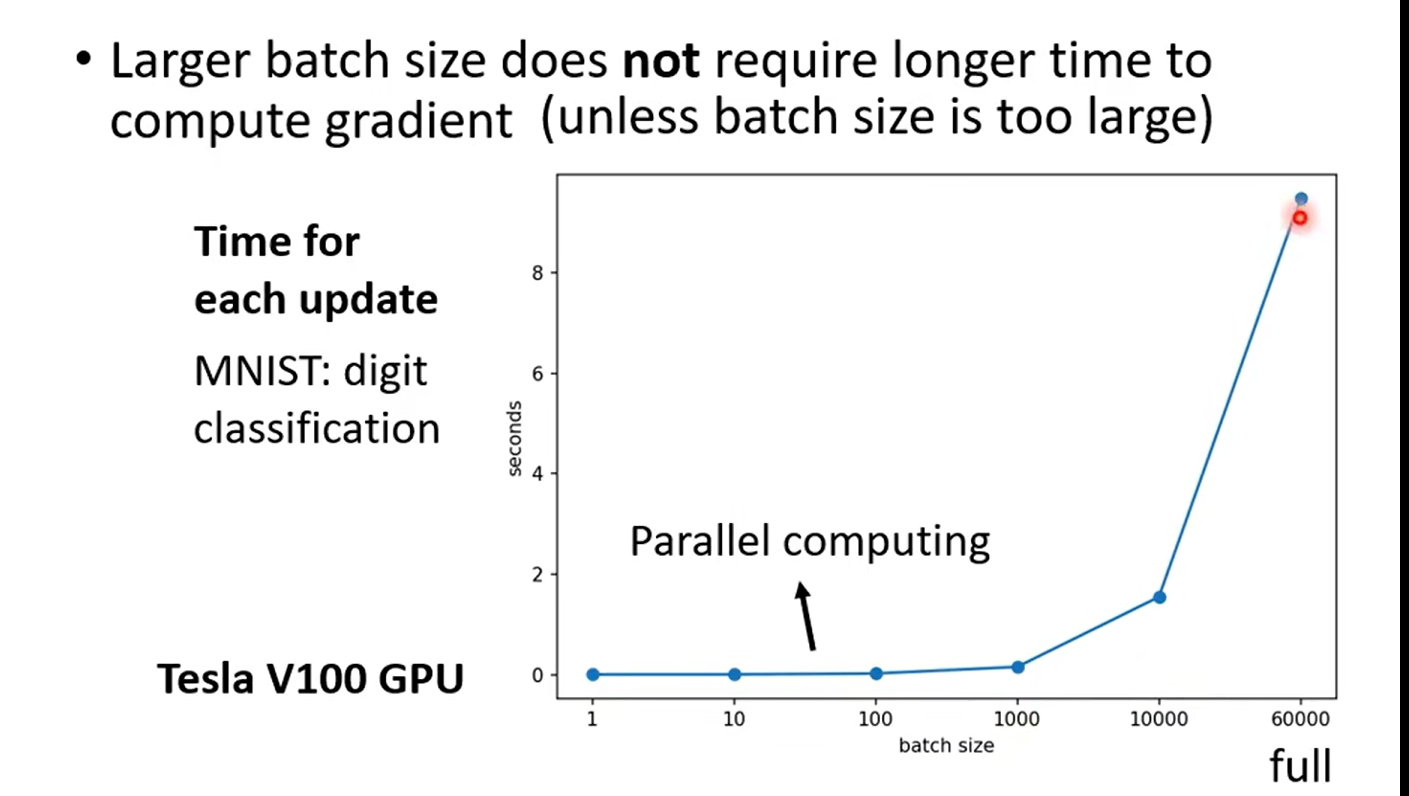
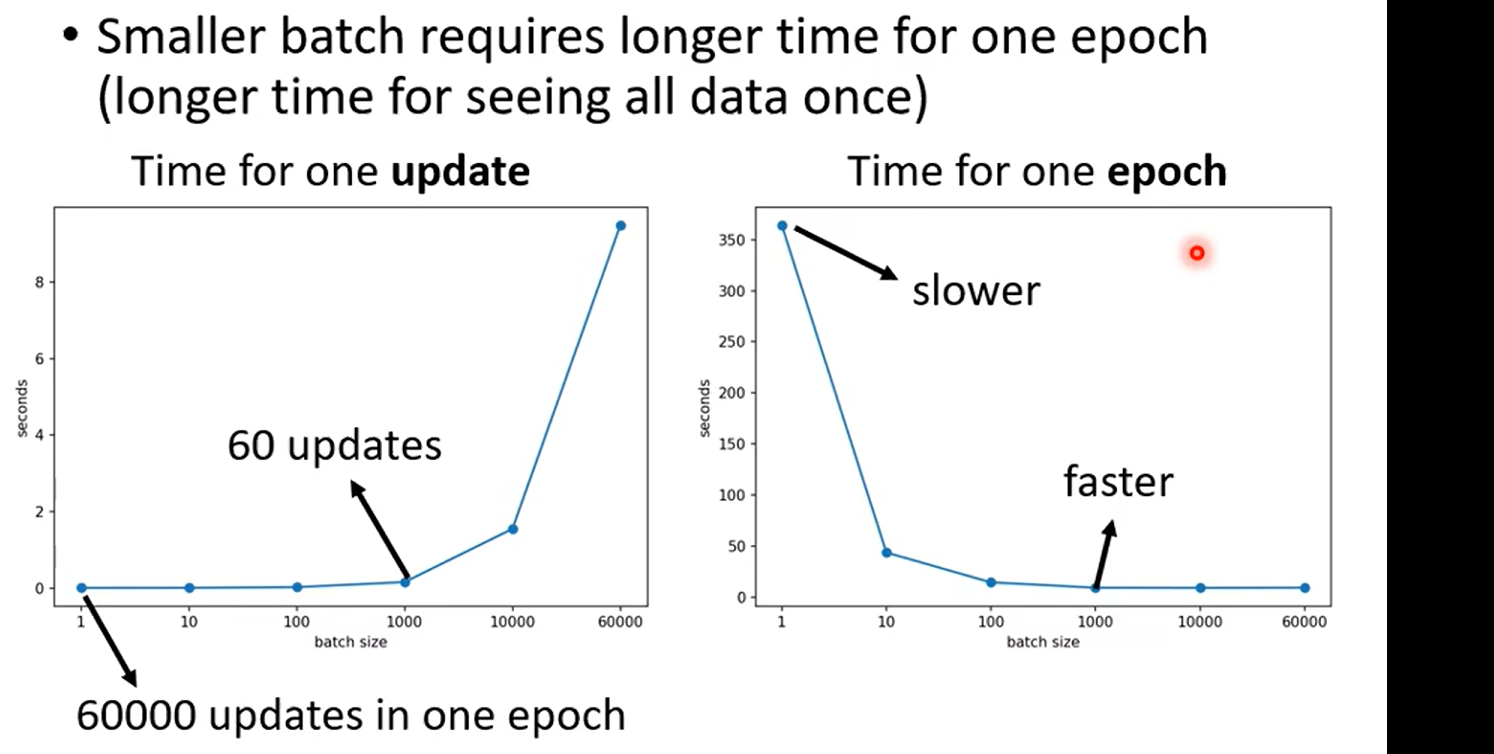

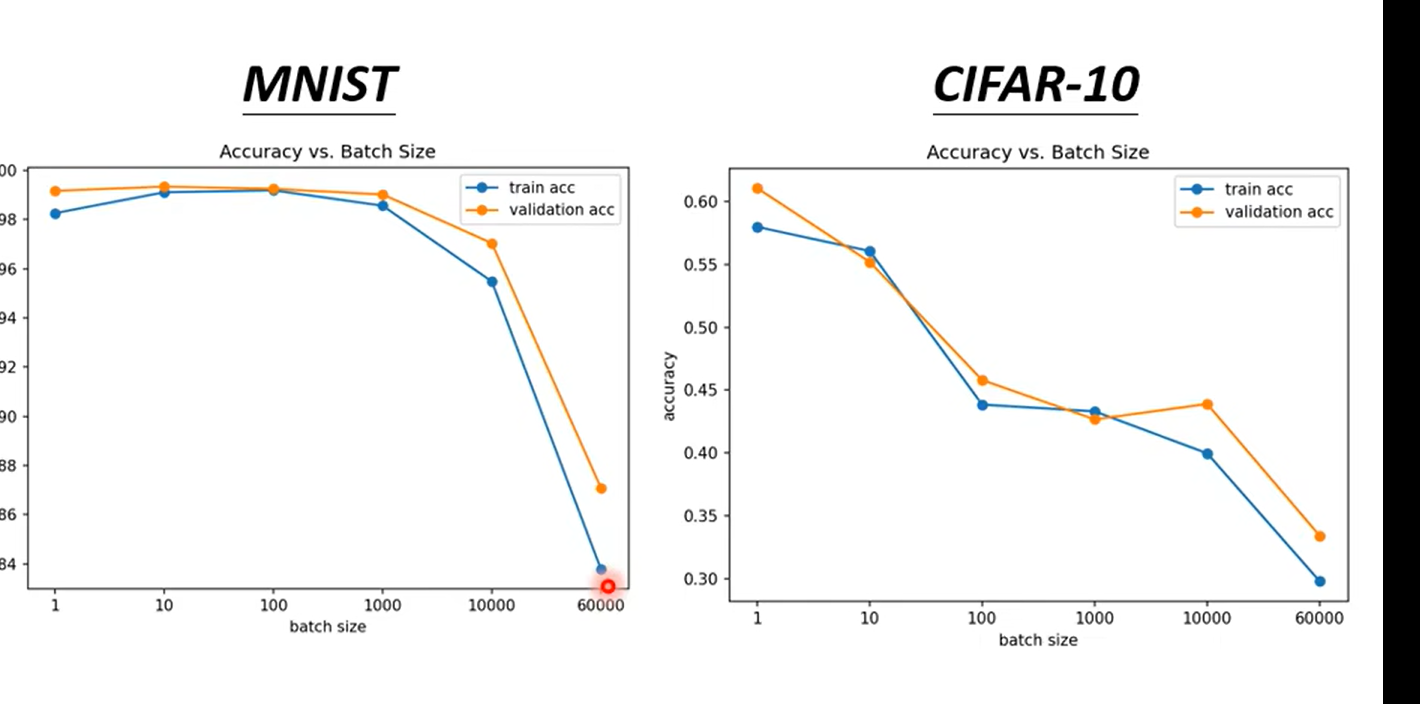

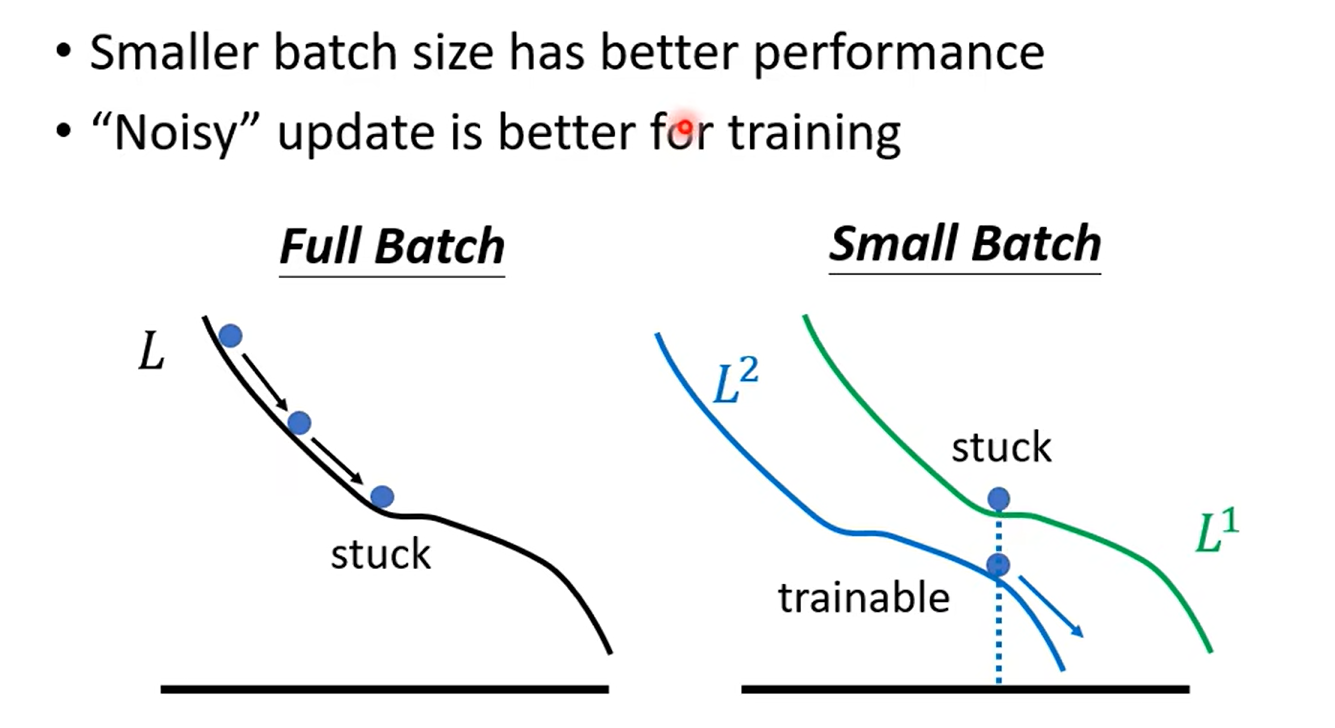
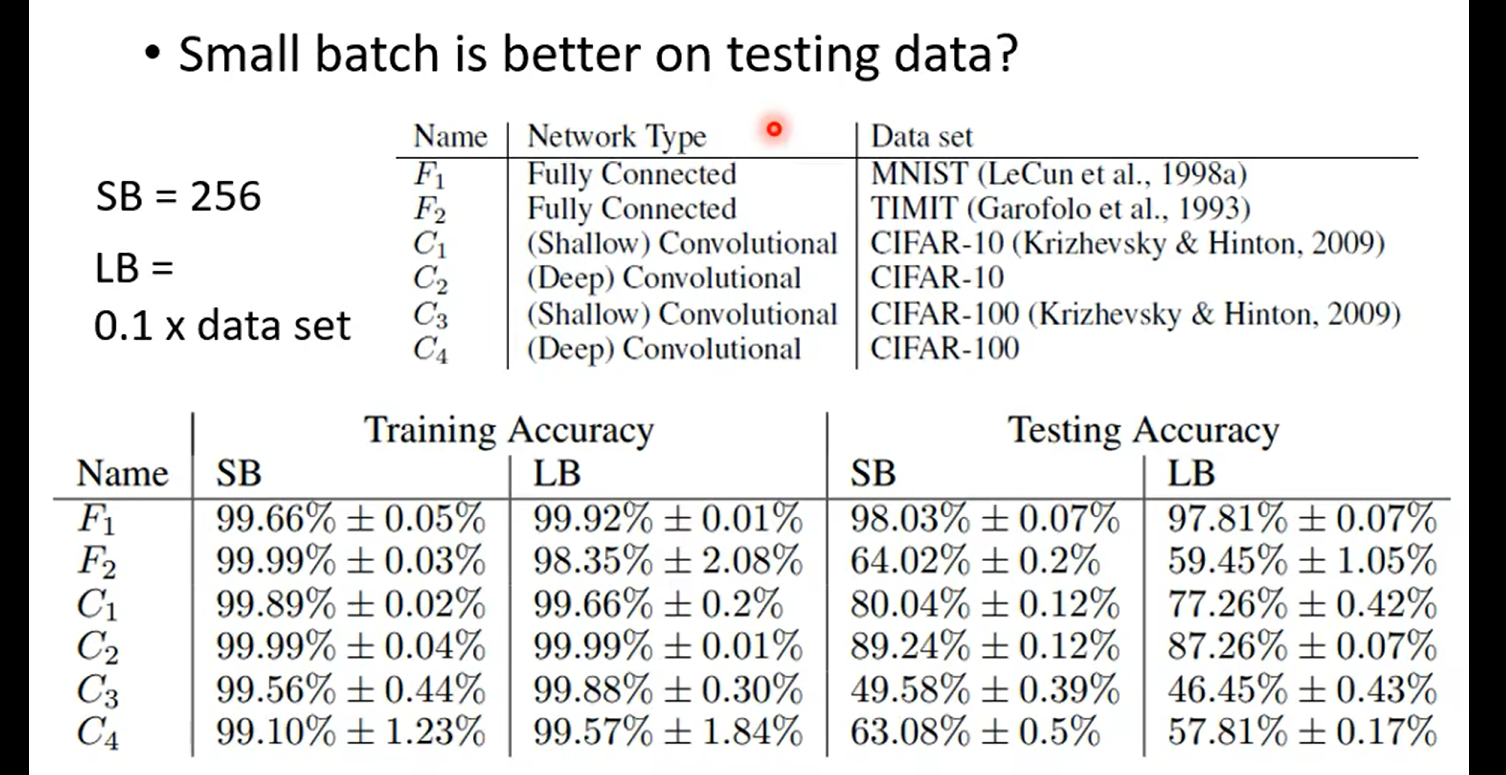
over fitting: 比较train 和test
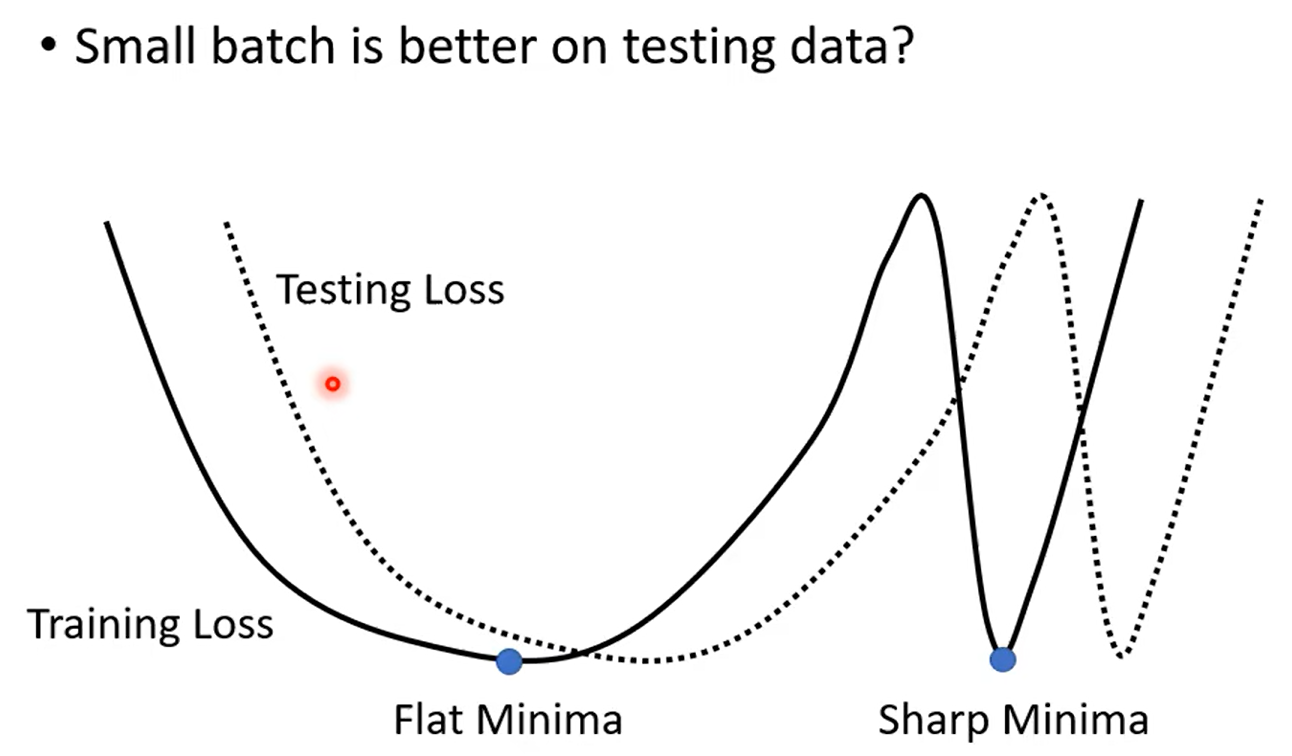
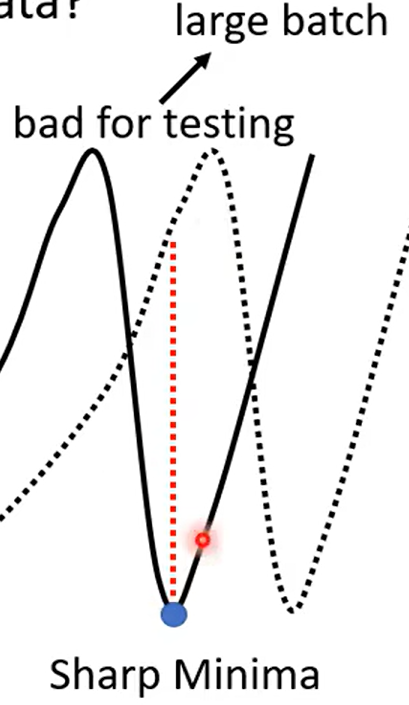
| Aspect | Small Batch Size(100个样本) | Large Batch Size(10000个样本) |
|---|---|---|
| Speed for one update (no parallel) | Faster | Slower |
| Speed for one update (with parallel) | Same | Same (not too large) |
| Time for one epoch | Slower | Faster |
| Gradient | Noisy | Stable |
| Optimization | Better | Worse |
| Generalization | Better | Worse |
batch is a hyperparameter……

Momentum
惯性
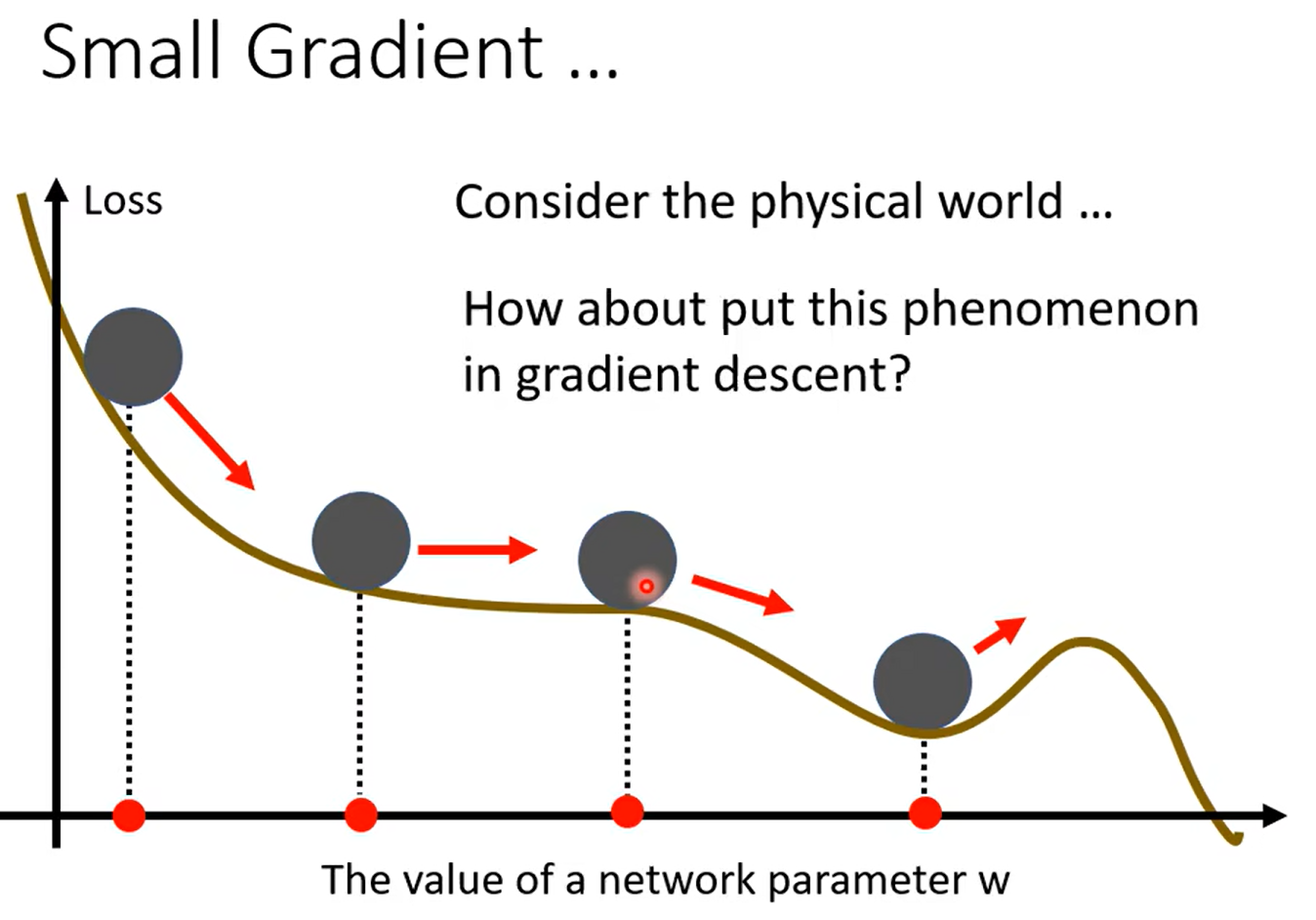
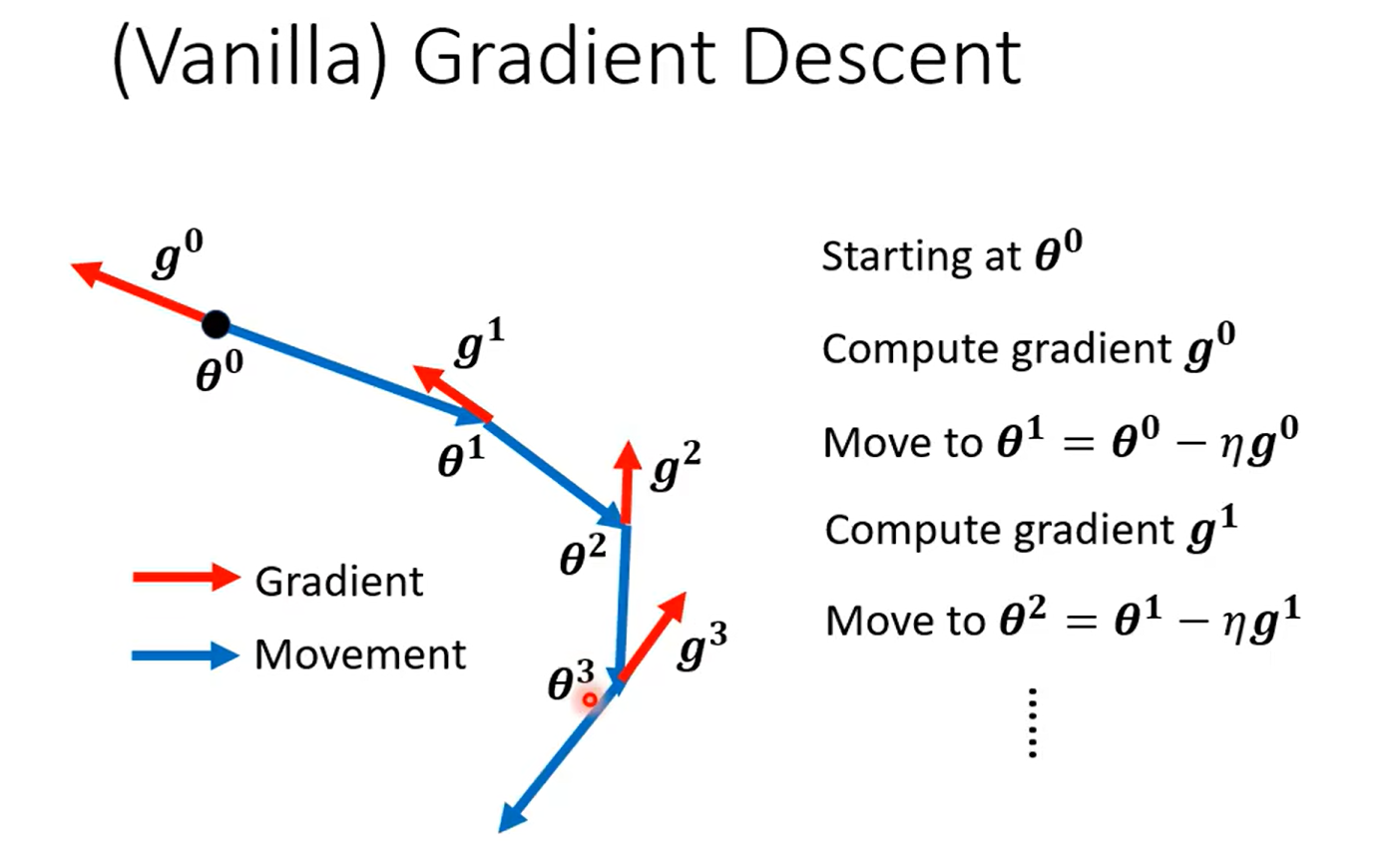
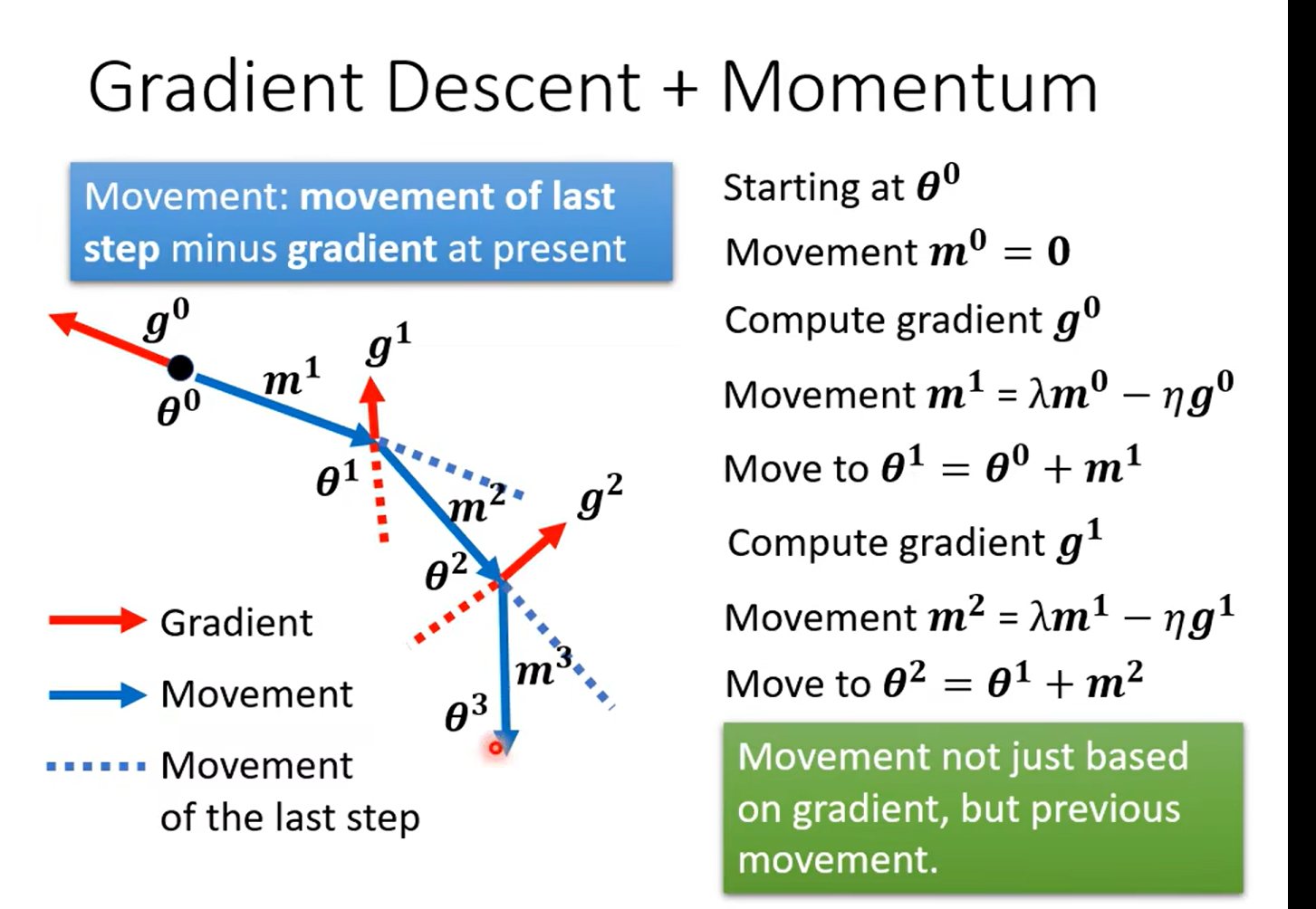
知道学到这里想到什么嘛……粒子群算法的公式不知道你们有没有了解,看下面那个w*vi 有没有感觉这种思想还挺常见的,用来做局部最小值的优化的

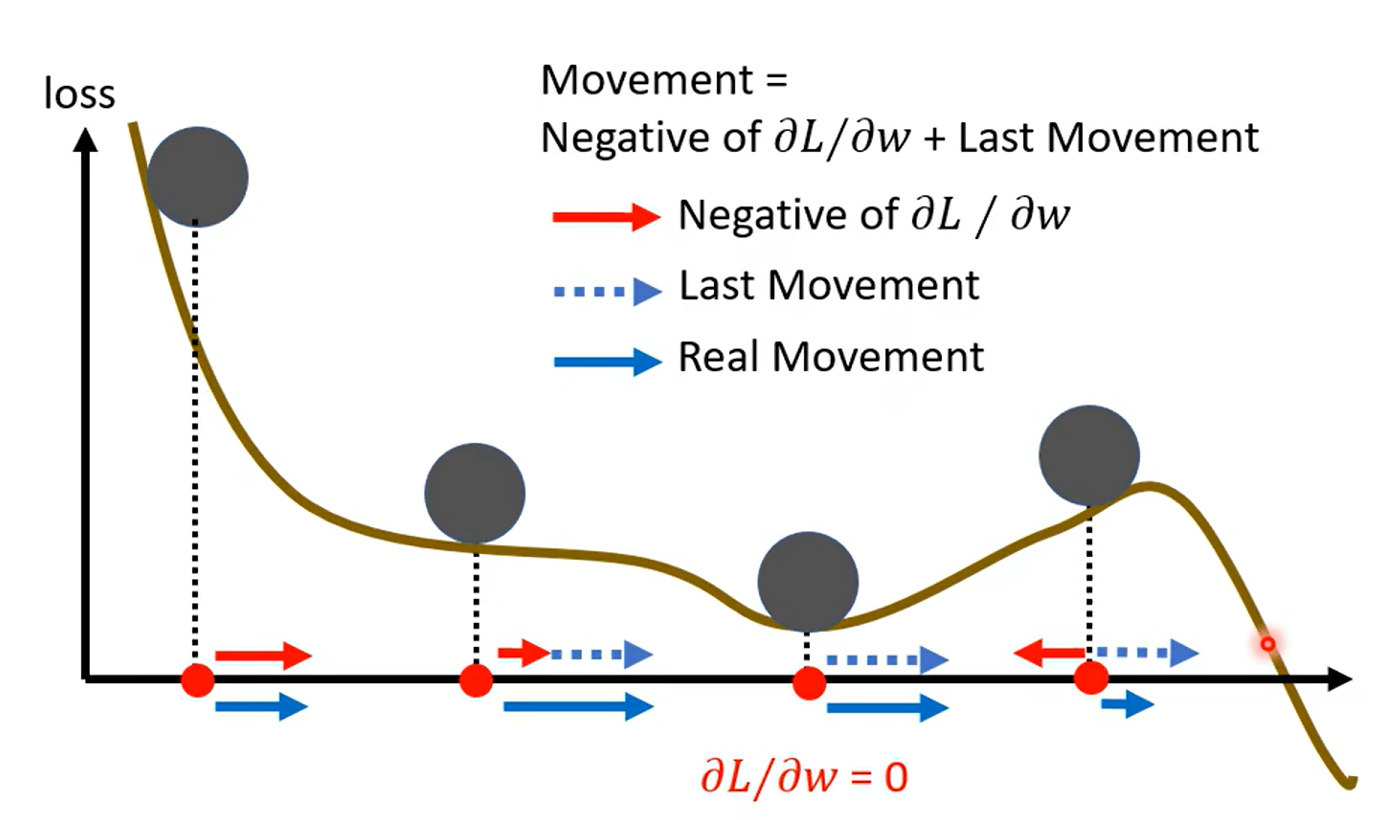
concluding:





)






)






、文件(File)和IO)


