矩阵转置算子优化
矩阵转置是一种基础的矩阵操作, 即将二维矩阵的行列进行反转.
本文主要围绕行主序的二维单精度矩阵的转置考虑相关的优化.
以下 kernel 笔者均是在 NVIDIA V100 (7.0 算力) 上进行测试的, 且选择矩阵的行列维度大小为 M=2300 N=1500.
Version 0. 朴素实现
__global__ void mat_transpose_kernel_v0(const float* idata, float* odata, int M, int N) {const int x = blockIdx.x * blockDim.x + threadIdx.x;const int y = blockIdx.y * blockDim.y + threadIdx.y;if (y < M && x < N) {odata[x * M + y] = idata[y * N + x];}
}void mat_transpose_v0(const float* idata, float* odata, int M, int N) {constexpr int BLOCK_SZ = 16;dim3 block(BLOCK_SZ, BLOCK_SZ);dim3 grid((N + BLOCK_SZ - 1) / BLOCK_SZ, (M + BLOCK_SZ - 1) / BLOCK_SZ));mat_transpose_kernel_v0<<<grid, block>>>(idata, odata, M, N);
}
矩阵转置的朴素实现非常直观, 思路即使用二维的线程/线程块排布, 让每个线程负责一个矩阵元素的转置. 实现上, 只需要将矩阵的行列索引 x y 进行反转即可.
需要注意的是 grid 和 block 的中维度设置与多维数组中的表示是相反的, 即 grid.x 应该对应 N 维度, grid.y 应该对应 M 维度.
| Version | 用时(us) | 内存带宽(GB/s) | 带宽利用率(%) | 加速比 |
|---|---|---|---|---|
| v0 | 84.90 | 399.92 | 56.38 |
结合矩阵转置的逻辑以及 Nsight Compute 容易判断出, 矩阵转置本身是一个 memory-bound 的 kernel, 因为其核心是完成矩阵内存排布的转换, 这个过程基本不涉及计算, 因此对该 kernel 优化很重要的一点就是提高访存性能.
朴素实现直接操作矩阵所在的 GMEM, 直观看来, 矩阵转置不会涉及数据的重用, 直接操作 GMEM 本身没有问题, 但此时应该注意 GMEM 的访存特性, 其中很重要的即 GMEM 的访存合并, 即连续线程访问的 GMEM 中的数据地址是连续的, 可以将多个线程的内存访问合并为一个(或多个)内存访问, 从而减少访存次数, 提高带宽利用率.
在 Version 0 的 kernel 中, 容易看出读取时 idata[y * N + x] 是访存合并的, 因为连续线程对应的 x 是连续的, 即访问矩阵同一行连续的列; 但是写入时 odata[x * M + y] 并不是访存合并的, 因为转置后连续线程写入的是同一列连续的行, 但由于内存布局是行主序的, 因此此时每个线程访问的地址实际上并不连续, 地址差 N, 因此对 GMEM 访存性能有很大影响.
Version 1. 利用共享内存合并访存
template <int BLOCK_SZ>
__global__ void mat_transpose_kernel_v1(const float* idata, float* odata, int M, int N) {const int bx = blockIdx.x, by = blockIdx.y;const int tx = threadIdx.x, ty = threadIdx.y;__shared__ float sdata[BLOCK_SZ][BLOCK_SZ];int x = bx * BLOCK_SZ + tx;int y = by * BLOCK_SZ + ty;if (y < M && x < N) {sdata[ty][tx] = idata[y * N + x];}__syncthreads();x = by * BLOCK_SZ + tx;y = bx * BLOCK_SZ + ty;if (y < N && x < M) {odata[y * M + x] = sdata[tx][ty];}
}void mat_transpose_v1(const float* idata, float* odata, int M, int N) {constexpr int BLOCK_SZ = 16;dim3 block(BLOCK_SZ, BLOCK_SZ);dim3 grid(Ceil(N, BLOCK_SZ), Ceil(M, BLOCK_SZ));mat_transpose_kernel_v1<BLOCK_SZ><<<grid, block>>>(idata, odata, M, N);
}
Version 0 的 kernel 存在的问题是写入 GMEM 时访存不合并, 因此需要一种方式让写入 GMEM 时仍然保持线程的访存连续, 在 Version 1 中, 便使用了 SMEM 用来中转来实现访存合并.
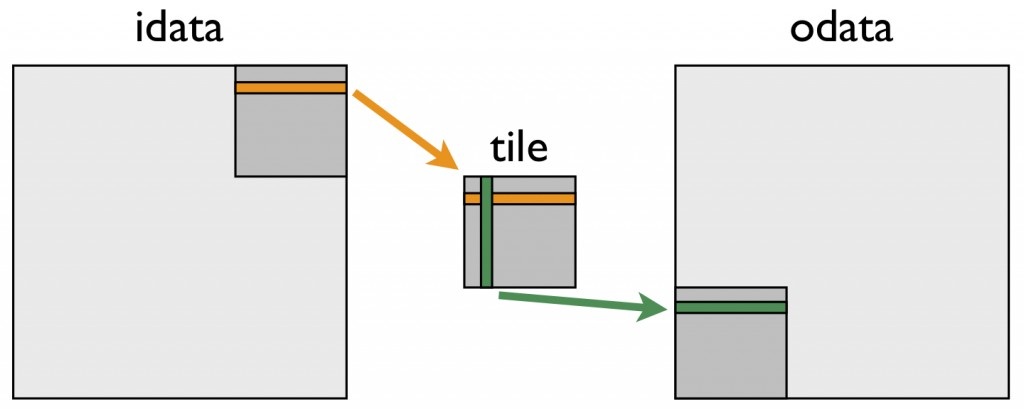
Version 1 的核心思想可以使用上图进行表示, 中间的 “tile” 即可理解为存在 SMEM 的数据分片.
在读取矩阵阶段, 操作与 Version 0 一致, 区别在于将数据直接写入 SMEM 中, 对应上图橙色部分. 接着通过设置 x = by * BLOCK_SZ + tx; y = bx * BLOCK_SZ + ty; 两条语句进行了索引的重计算, 进行了线程块索引 bx 和 by 交换, 对应上图右上角的数据分片转置后成为了左下角的数据分片. 由于此时 tx 和 ty 并没有交换, 因此按照 odata[y * M + x] 写入 GMEM 时, 访存是合并的, 但需要读取 SMEM 时 tx 与 ty 进行交换, 实现数据分片内的转置, 对应上图绿色部分.
| Version | 用时(us) | 内存带宽(GB/s) | 带宽利用率(%) | 加速比 |
|---|---|---|---|---|
| v0 | 84.90 | 399.92 | 56.38 | |
| v1 | 47.49 | 610.57 | 71.07 | 1.79 |
可以看到, Version 1 相比于 Version 0 性能有了很大提升. 如下图所示, 通过 Nsight Compute 也能看到 Version 1 (右) 比 Version 0 (左) 在读取写入 GMEM 的带宽上都有所提升.
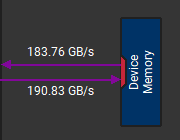

在 Version 1 中, 引入了对 SMEM 的访存, 因此需要特别关注 bank conflict 的问题. 对于 SMEM 的写入, sdata[ty][tx], 由于 BLOCK_SZ 为 16, 32 个线程负责 SMEM 矩阵分片的两行 32 个元素, 对应 32 个 bank, 因此没有 bank conflict. 而对于 SMEM 的读取, sdata[tx][ty], 由于是按列读取 SMEM 的, threadIdx 差 1 的线程访问的数据差 BLOCK_SZ, 即导致threadIdx 差 2 的线程访问的数据落到同一 bank 的不同地址, 从而造成 16 路的 bank conflict.
因此, Version 1 中读取 SMEM 引起的 bank conflict 影响 SMEM 的访存效率, 进而影响 kernel 的性能.
Version 2. 利用 padding 解决 bank conflict
template <int BLOCK_SZ>
__global__ void mat_transpose_kernel_v2(const float* idata, float* odata, int M, int N) {const int bx = blockIdx.x, by = blockIdx.y;const int tx = threadIdx.x, ty = threadIdx.y;__shared__ float sdata[BLOCK_SZ][BLOCK_SZ+1]; // paddingint x = bx * BLOCK_SZ + tx;int y = by * BLOCK_SZ + ty;if (y < M && x < N) {sdata[ty][tx] = idata[y * N + x];}__syncthreads();x = by * BLOCK_SZ + tx;y = bx * BLOCK_SZ + ty;if (y < N && x < M) {odata[y * M + x] = sdata[tx][ty];}
}void mat_transpose_v2(const float* idata, float* odata, int M, int N) {constexpr int BLOCK_SZ = 16;dim3 block(BLOCK_SZ, BLOCK_SZ);dim3 grid(Ceil(N, BLOCK_SZ), Ceil(M, BLOCK_SZ));mat_transpose_kernel_v2<BLOCK_SZ><<<grid, block>>>(idata, odata, M, N);
}
Version 2 的代码相比于 Version 1 仅在 SMEM 内存分配时进行了变动, 将大小改为了 sdata[BLOCK_SZ][BLOCK_SZ+1], 即列维度上加入了 1 元素大小的 padding.
此时, 对于读取 SMEM 的 sdata[tx][ty], threadIdx 差 1 的线程访问的数据差 BLOCK_SZ+1, 即 17, 由于 17 与 32 互质, 因此不会有 bank conflict. 值得一提的是, 对于写入 SMEM 的 sdata[ty][tx], 由于有 1 个 padding, warp 中 lane 31 与 lane 0 访问的元素恰好差 31+1=32 个元素, 会有 1 个 bank conflict.
整体上, Version 2 通过 padding 的方法有效避免了读取 SMEM 时的 bank conflict.
| Version | 用时(us) | 内存带宽(GB/s) | 带宽利用率(%) | 加速比 |
|---|---|---|---|---|
| v0 | 84.90 | 399.92 | 56.38 | |
| v1 | 47.49 | 610.57 | 71.07 | 1.79 |
| v2 | 44.38 | 627.31 | 72.47 | 1.91 |
Version 2 相比 Version 1性能有了一定的提升. 如下图所示, 通过 Nsight Compute 也能看到 Version 2 (右) 比 Version 1 (左) 的 bank conflict 总数明显下降, 其中读取 SMEM 时的 bank conflict (第一行) 大幅降低, 而写入 SMEM 时的 bank conflict (第二行) 有一定上升, 也与上文分析的相匹配.
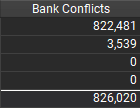

Version 3. 增加每个线程处理的元素个数
template <int BLOCK_SZ, int NUM_PER_THREAD>
__global__ void mat_transpose_kernel_v3(const float* idata, float* odata, int M, int N) {const int bx = blockIdx.x, by = blockIdx.y;const int tx = threadIdx.x, ty = threadIdx.y;__shared__ float sdata[BLOCK_SZ][BLOCK_SZ+1];int x = bx * BLOCK_SZ + tx;int y = by * BLOCK_SZ + ty;constexpr int ROW_STRIDE = BLOCK_SZ / NUM_PER_THREAD;if (x < N) {#pragma unrollfor (int y_off = 0; y_off < BLOCK_SZ; y_off += ROW_STRIDE) {if (y + y_off < M) {sdata[ty + y_off][tx] = idata[(y + y_off) * N + x]; }}}__syncthreads();x = by * BLOCK_SZ + tx;y = bx * BLOCK_SZ + ty;if (x < M) {for (int y_off = 0; y_off < BLOCK_SZ; y_off += ROW_STRIDE) {if (y + y_off < N) {odata[(y + y_off) * M + x] = sdata[tx][ty + y_off];}}}
}void mat_transpose_v3(const float* idata, float* odata, int M, int N) {constexpr int BLOCK_SZ = 32;constexpr int NUM_PER_THREAD = 4;dim3 block(BLOCK_SZ, BLOCK_SZ/NUM_PER_THREAD);dim3 grid(Ceil(N, BLOCK_SZ), Ceil(M, BLOCK_SZ));mat_transpose_kernel_v3<BLOCK_SZ, NUM_PER_THREAD><<<grid, block>>>(idata, odata, M, N);
}
Version 3 相比于 Version 2, 增加了每个线程处理的元素个数, 即由先前的每个线程处理 1 个元素的转置, 变为处理 NUM_PER_THREAD 个元素的转置. 该实现主要是参考了 英伟达的技术博客.
在实现上, 同样保持原本 256 线程的线程块大小, 设置每个线程处理 4 个元素, 则每个线程块数据分片的大小调整为 32×32, 而线程块的线程采取 8×32 的二维排布, 因此需要在行维度上需要迭代 4 次完成转置.
考虑 Version 3 相比于 Version 2 的优势, 主要是在保持线程块中线程数量不变的情况下, 处理的线程块数据分片大小变大, 这样会减少线程网格中启动的线程块数量, 而增大了每个线程的计算强度; 此外, 由于 BLOCK_SZ 变为 32, Version 2 中写入 SMEM 的 1 个 bank conflict 也可以被避免.
这让笔者想到了 Reduce 算子中也会考虑增加每个线程处理的元素来提高性能, 笔者主观的感觉是对于这种计算强度比较低的 kernel, 增加线程处理的元素个数即计算强度, 一定程度上能增大 GPU 中计算与访存的掩盖, 并配合循环展开提高指令级并行; 此外, 由于线程块数量的减少, 能在相对少的 wave 中完成计算, 减少 GPU 的线程块调度上可能也会带来性能的收益.
| Version | 用时(us) | 内存带宽(GB/s) | 带宽利用率(%) | 加速比 |
|---|---|---|---|---|
| v0 | 84.90 | 399.92 | 56.38 | |
| v1 | 47.49 | 610.57 | 71.07 | 1.79 |
| v2 | 44.38 | 627.31 | 72.47 | 1.91 |
| v3 | 39.68 | 699.05 | 81.43 | 2.14 |
通过测试可以看出, Version 3 相比 Version 2 又有了一定的性能提升, 内存带宽也有了进一步的提高.
Version 3.5 向量化读取
#define FETCH_CFLOAT4(p) (reinterpret_cast<const float4*>(&(p))[0])
#define FETCH_FLOAT4(p) (reinterpret_cast<float4*>(&(p))[0])template <int BLOCK_SZ>
__global__ void mat_transpose_kernel_v3_5(const float* idata, float* odata, int M, int N) {const int bx = blockIdx.x, by = blockIdx.y;const int tx = threadIdx.x, ty = threadIdx.y;__shared__ float sdata[BLOCK_SZ][BLOCK_SZ];int x = bx * BLOCK_SZ + tx * 4;int y = by * BLOCK_SZ + ty;if (x < N && y < M) {FETCH_FLOAT4(sdata[ty][tx * 4]) = FETCH_CFLOAT4(idata[y * N + x]);}__syncthreads();x = by * BLOCK_SZ + tx * 4;y = bx * BLOCK_SZ + ty;float tmp[4];if (x < M && y < N) {#pragma unrollfor (int i = 0; i < 4; ++i) {tmp[i] = sdata[tx * 4 + i][ty];}FETCH_FLOAT4(odata[y * M + x]) = FETCH_FLOAT4(tmp);}
}void mat_transpose_v3_5(const float* idata, float* odata, int M, int N) {constexpr int BLOCK_SZ = 32;dim3 block(BLOCK_SZ / 4, BLOCK_SZ);dim3 grid(Ceil(N, BLOCK_SZ), Ceil(M, BLOCK_SZ));mat_transpose_kernel_v3_5<BLOCK_SZ><<<grid, block>>>(idata, odata, M, N);
}
Version 3 是通过在行维度上迭代多次实现了每个线程处理多个元素的目的. 这里笔者尝试使用向量化访存的形式在列维度上让每个线程负责连续的多个元素.
在实现上, BLOCK_SZ 仍然是 32, 即线程块数据分片的大小保持 32×32, 而线程块的线程采取 32×8 的二维排布, 这是因为列维度上使用向量化访存一次读取 4 个元素.
但是, 向量化访存也带了一些问题, 首先向量化访存需要地址对齐, 因此不能使用 Version 2 中的 padding 方式, 因为 padding 的 1 个元素会导致访问元素并不是 4 个元素地址对齐的; 另一方面, 在从 SMEM 转置写入 GMEM 输出时, 是按列读取 SMEM 的, 无法直接使用向量化访存, 因此需要逐元素读取到寄存器后再向量化访存写入 GMEM.
| Version | 用时(us) | 内存带宽(GB/s) | 带宽利用率(%) | 加速比 |
|---|---|---|---|---|
| v0 | 84.90 | 399.92 | 56.38 | |
| v1 | 47.49 | 610.57 | 71.07 | 1.79 |
| v2 | 44.38 | 627.31 | 72.47 | 1.91 |
| v3 | 39.68 | 699.05 | 81.43 | 2.14 |
| v3.5 | 42.46 | 679.80 | 82.64 | 2.00 |
通过测试可以看出, Version 3.5 的性能相比 Version 2 有一定提升, 但并不如 Version 3., 受益于向量化访存, 带宽相比于 Version 2 也有一定提升, 但由于无法 padding 避免 bank conflict, 也导致其性能并不如 Version 3.
Version 4. 减少条件分支
template <int BLOCK_SZ, int NUM_PER_THREAD>
__global__ void mat_transpose_kernel_v4(const float* idata, float* odata, int M, int N) {const int bx = blockIdx.x, by = blockIdx.y;const int tx = threadIdx.x, ty = threadIdx.y;__shared__ float sdata[BLOCK_SZ][BLOCK_SZ+1];int x = bx * BLOCK_SZ + tx;int y = by * BLOCK_SZ + ty;constexpr int ROW_STRIDE = BLOCK_SZ / NUM_PER_THREAD;if (x < N) {if (y + BLOCK_SZ <= M) {#pragma unrollfor (int y_off = 0; y_off < BLOCK_SZ; y_off += ROW_STRIDE) {sdata[ty + y_off][tx] = idata[(y + y_off) * N + x]; }} else {for (int y_off = 0; y_off < BLOCK_SZ; y_off += ROW_STRIDE) {if (ty + y_off < M) {sdata[ty + y_off][tx] = idata[(y + y_off) * N + x];}}}}__syncthreads();x = by * BLOCK_SZ + tx;y = bx * BLOCK_SZ + ty;if (x < M) {if (y + BLOCK_SZ <= N) {#pragma unrollfor (int y_off = 0; y_off < BLOCK_SZ; y_off += ROW_STRIDE) {odata[(y + y_off) * M + x] = sdata[tx][ty + y_off];}} else {for (int y_off = 0; y_off < BLOCK_SZ; y_off += ROW_STRIDE) {if (y + y_off < N) {odata[(y + y_off) * M + x] = sdata[tx][ty + y_off];}}}}
}void mat_transpose_v4(const float* idata, float* odata, int M, int N) {constexpr int BLOCK_SZ = 32;constexpr int NUM_PER_THREAD = 4;dim3 block(BLOCK_SZ, BLOCK_SZ/NUM_PER_THREAD);dim3 grid(Ceil(N, BLOCK_SZ), Ceil(M, BLOCK_SZ));mat_transpose_kernel_v4<BLOCK_SZ, NUM_PER_THREAD><<<grid, block>>>(idata, odata, M, N);
}
Version 4 参考了 CUTLASS 中 N C H W NCHW NCHW 与 N H W C NHWC NHWC 格式转换的 kernel, 该 kernel 本质上就是 C C C 与 H W HW HW 两个维度的矩阵转置.
在实现上, Version 4 的 kernel 与 Version 3 的核心思路是一致的, 仍然是每个线程需要行维度上迭代多次. 不同的是, 该实现对分支语句的判断进行了更加细致的处理. 具体而言, 在 Version 3 中, 每个线程的每次行迭代都要进行 y + y_off 的判断, 即矩阵元素的范围检查, 但考虑大部分线程块的数据分片都是在矩阵内部的, 即不会越界, 那么执行多次范围检查就会比较多余. 在 Version 4 中, 会先检查 y + BLOCK_SZ <= M, 即如果该线程块的数据分片并不在矩阵边缘, 那么每次迭代时便无需再进行越界检查; 反之, 若数据分片位于矩阵边缘, 则需要和 Version 3 一样每次迭代时越界检查.
整体看来, 该实现虽然增加了代码复杂程度, 但会简化大部分线程块中迭代时的逻辑, 减少冗余的条件分支的判断次数.
| Version | 用时(us) | 内存带宽(GB/s) | 带宽利用率(%) | 加速比 |
|---|---|---|---|---|
| v0 | 84.90 | 399.92 | 56.38 | |
| v1 | 47.49 | 610.57 | 71.07 | 1.79 |
| v2 | 44.38 | 627.31 | 72.47 | 1.91 |
| v3 | 39.68 | 699.05 | 81.43 | 2.14 |
| v3.5 | 42.46 | 679.80 | 82.64 | 2.00 |
| v4 | 40.42 | 686.50 | 80.25 | 2.10 |
有意思的是, 在实际测试时, Version 4 的性能与 Version 3 很接近, 但与 Version 3 仍有略微的性能差距, 且带宽上也并没有 Version 3 高.
参考文献
- An Efficient Matrix Transpose in CUDA C/C++ | NVIDIA Technical Blog
- CUDA 编程入门之矩阵转置 - 知乎
- CUDA学习(二)矩阵转置及优化(合并访问、共享内存、bank conflict) - 知乎
- NVIDIA/cutlass - device_nchw_to_nhwc.h




)




)
:LocalAI本地使用Model gallery,对qwen模型进行配置,使用modescope源下载,本地运行速度快。特别简单!)

)
)





