dp(3) - 背包问题(上)

目录

简论

关于dp问题 :

​编辑

0-1背包问题

定义 :

例题 :

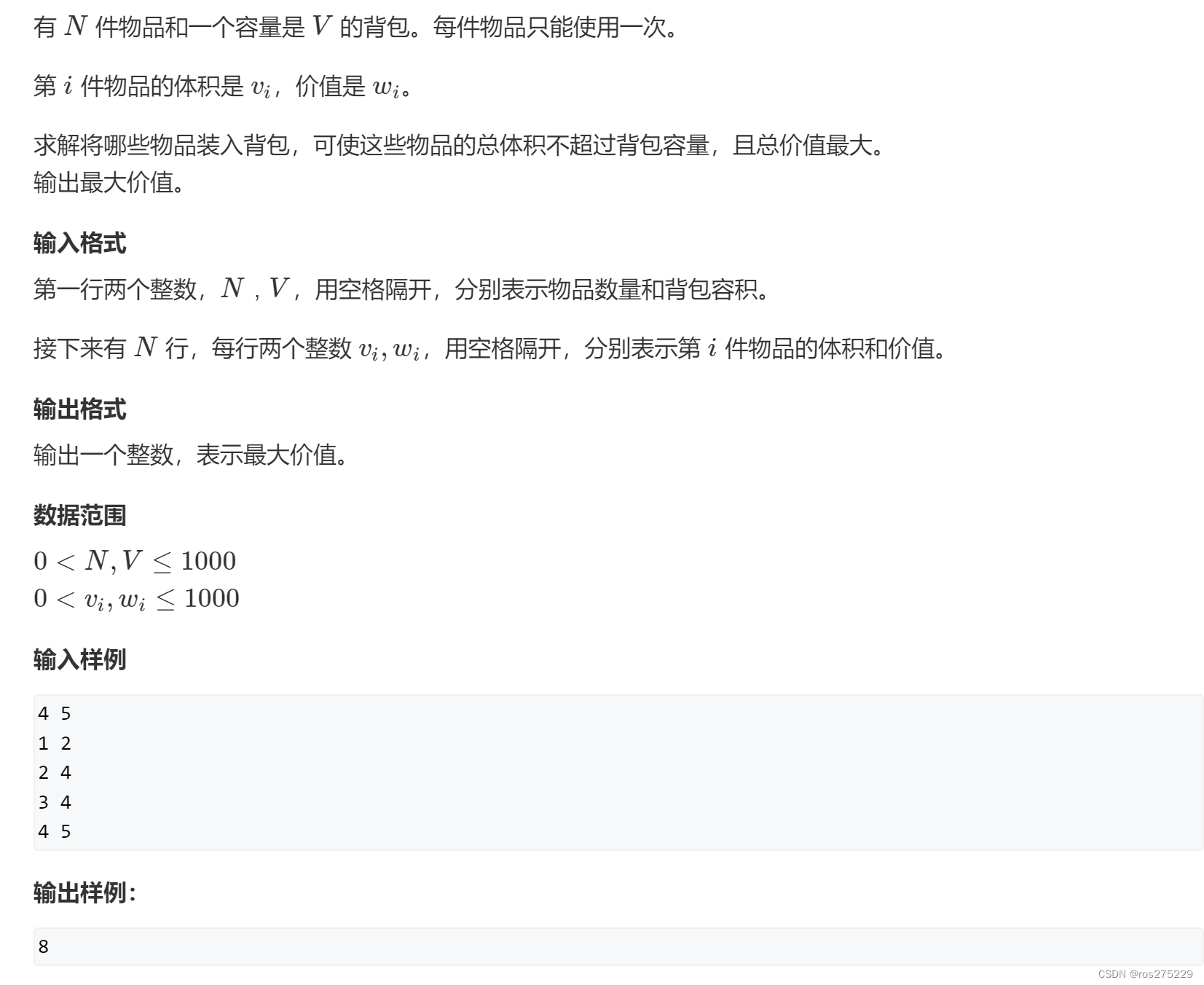
题面 :

​编辑

思路 :

代码(二维) :

代码(一维优化版):

完全背包问题

题目链接 :

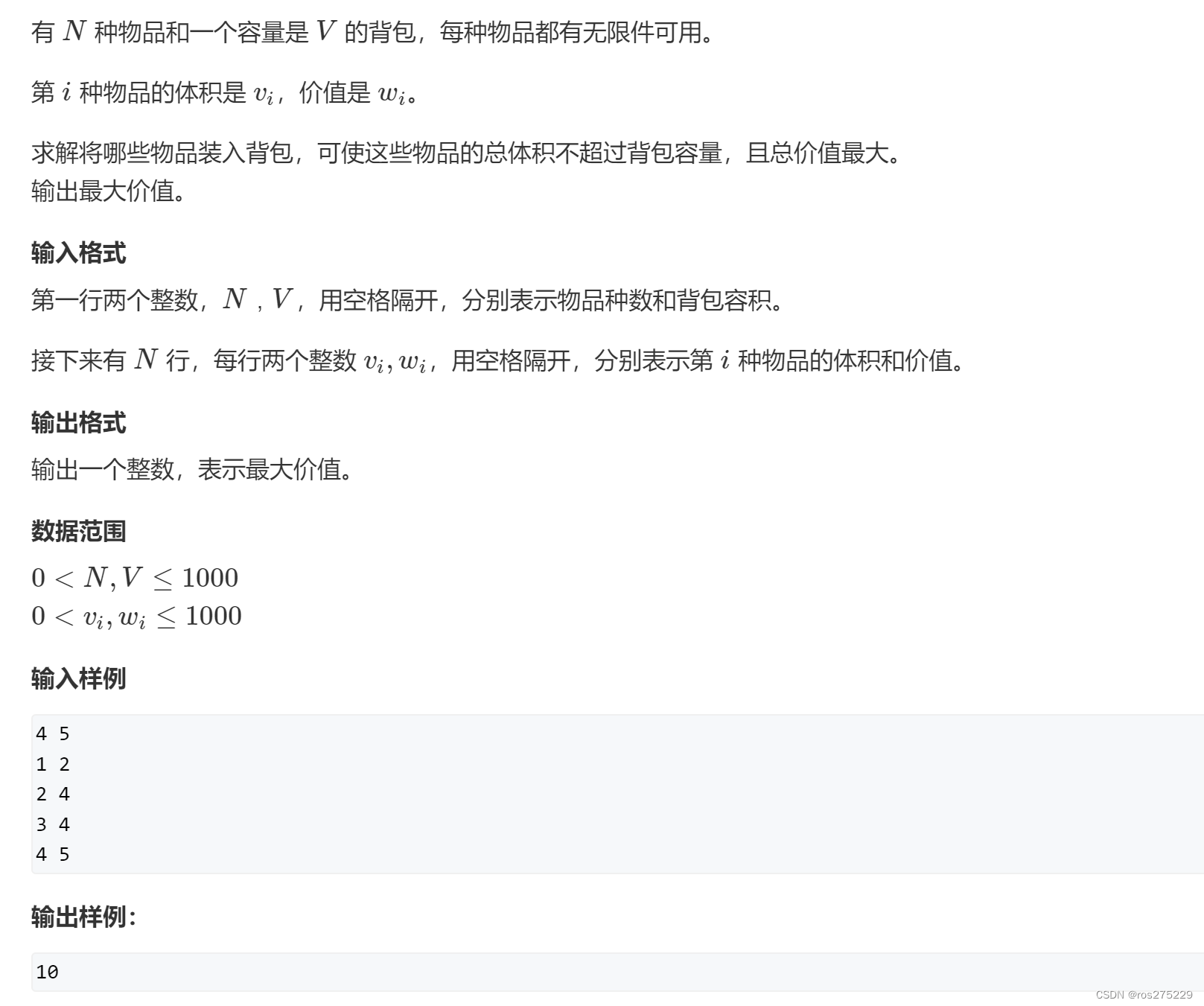
题面 :

​编辑

思路 :

代码(朴素) :

代码(优化) :

代码(一维优化) :

多重背包问题

题目链接 :

题面 :

​编辑

思考 :

代码 (朴素):

多重背包问题II

链接 :

思路 :

代码(二进制优化) :

分组背包问题

题目链接 :

思考 :

代码 (朴素):

代码(一维优化) :

简论

这篇将关于动态规划问题中的背包问题(上)，包括，01背包，完全背包，多重背包，分组背包的朴素代码和其优化的详细解答，主要基于acwing算法基础课动态规划讲解,欢迎留言讨论！！！

知识图谱 :

1.代码随想录

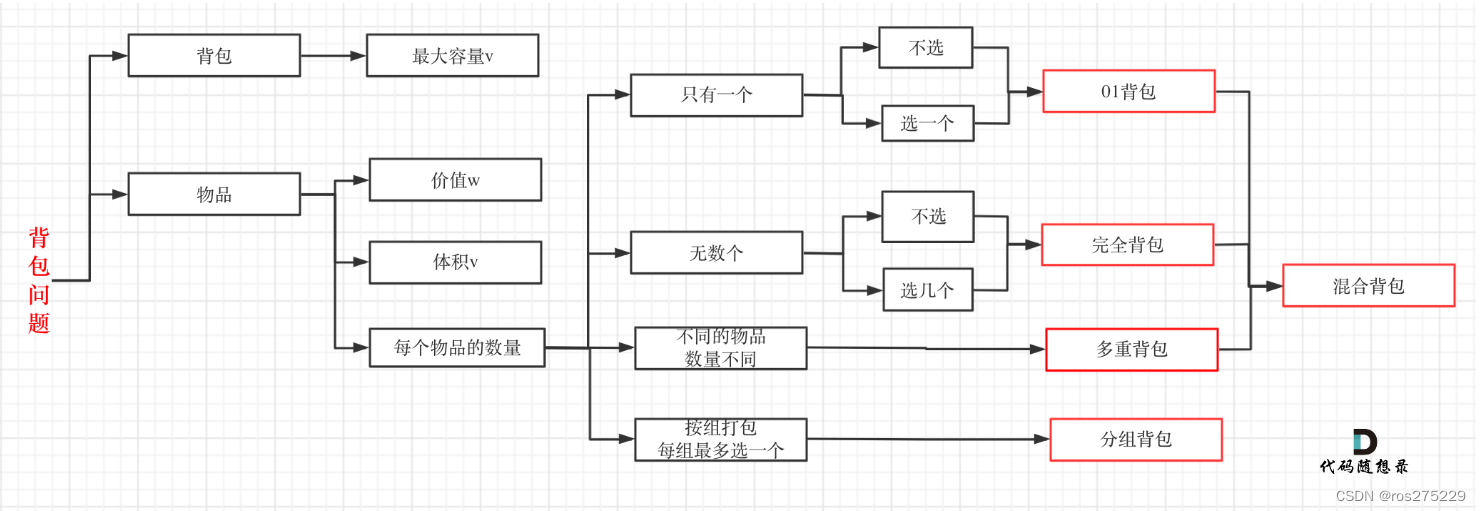
2.acwing

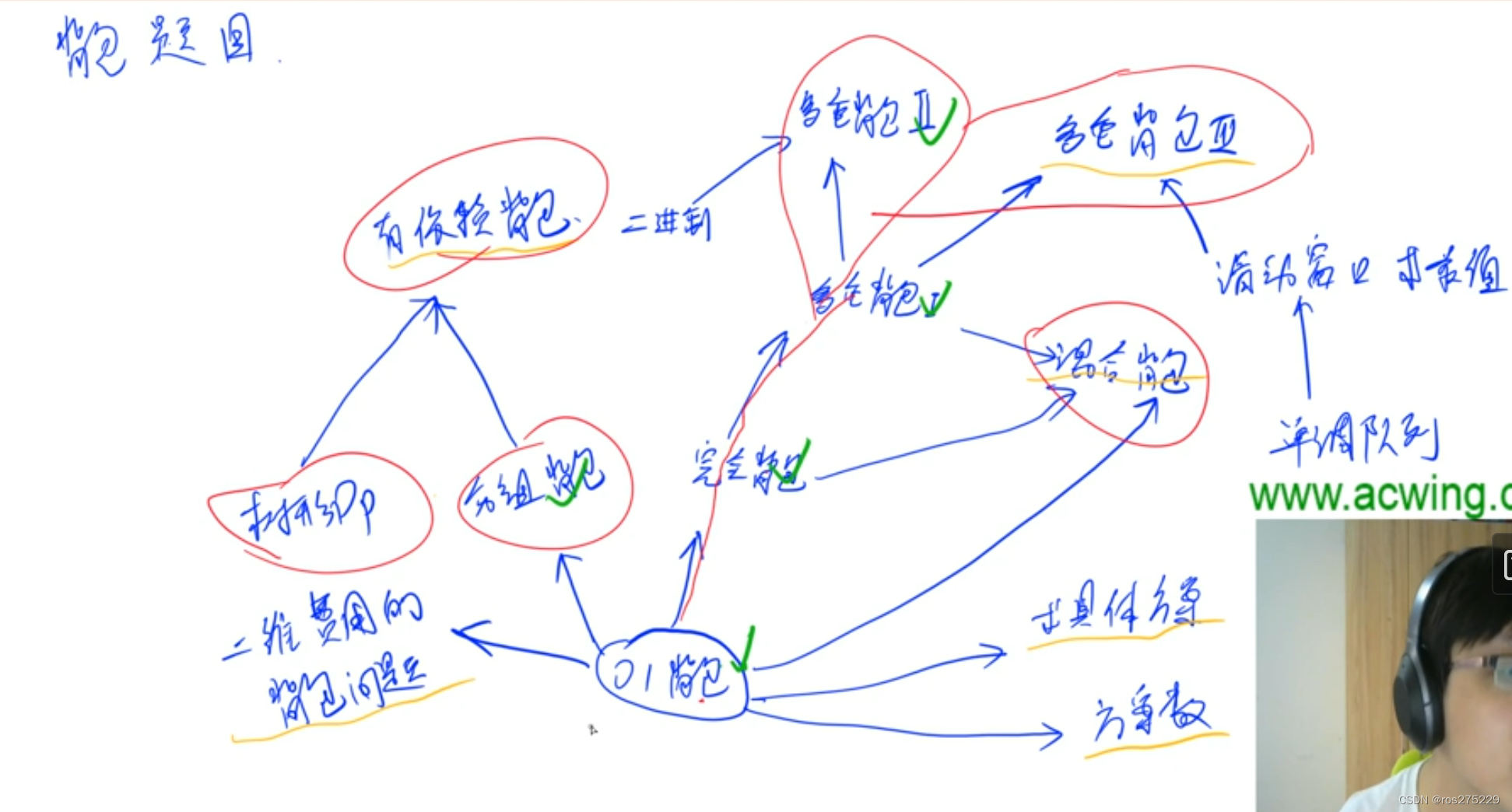
  • 01背包问题 : N个物品V空间容量，每个物品仅能用一次，v[i],w[i],是总价值最大

  • 完全背包问题 : 每件物品有无数个

  • 多重背包问题 : 每个物品si个；

  • 分组背包 : M组

关于dp问题 :

  • 先考虑状态表示 : 如f(i,j),又可以分为集合和属性 :

    • 集合 : 如在01背包问题中，f(i,j)表示只从前i个物品中选且满足总体积<=j的所有选法;

    • 属性 : 本题求得是最大值，也就是max,其它得还有min,数量等;

  • 再考虑状态计算,这一部分也就是考虑状态转移方程式,即f(i,j)能由那个状态得来；

    • 对应集合的划分，表示能分成的子集的集合；

    • 在01背包问题中，f(i,j)可以划分为含i和不含i的两种情况；

0-1背包问题

定义 :

给定一个容量为V的背包,现在有N个物品，每个物品的价值为vi,重量为wi,求选择一个或多个，再不超过容量的情况下，求每个物品最多选一次的前提下的最大价值;

例题 :

  • 2. 01背包问题 - AcWing题库

  • [NOIP2005 普及组] 采药 - 洛谷

题面 :

思路 :

重要变量&公式解释 f(i,j):表示所有选法集合中,只从前i个物品中选,并且总体积 ≤ j的选法的集合;它的值是这个集合中每一个选法的最大值.

状态转移方程 f [i] [j] = max(f(i-1,j), f(i-1,j-v[i])+w[i])

f(i-1 , j) : 不选第i个物品的集合中的最大值 f(i-1,j-v[i]) + w[i] : 选第i个物品的集合,但是直接求不容易求所在集合的属性,这里迂回打击一下,先将第i个物品的体积减去,求剩下集合中选法的最大值.

代码(二维) :

#include<iostream>
using namespace std;
const int N = 1010;
int v[N],w[N];
int dp[N][N];
int main(){int n,V;cin>>n>>V;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=1;j<=V;j++){dp[i][j] = dp[i-1][j];if(j>=v[i]) dp[i][j] = max(dp[i][j],dp[i-1][j-v[i]]+w[i]);}}cout << dp[n][V] << endl;return 0;
}

代码(一维优化版):

#include<iostream>
using namespace std;
const int N = 1010;
int v[N],w[N];
int dp[N];
int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=m;j>=v[i];j--){dp[j] = max(dp[j],dp[j-v[i]]+w[i]);}}cout << dp[m] << endl;return 0;
}

完全背包问题

题目链接 :

3. 完全背包问题 - AcWing题库

题面 :

思路 :

f(i,j)表示在前i个物品中选，且总体积不大于j的所有选法

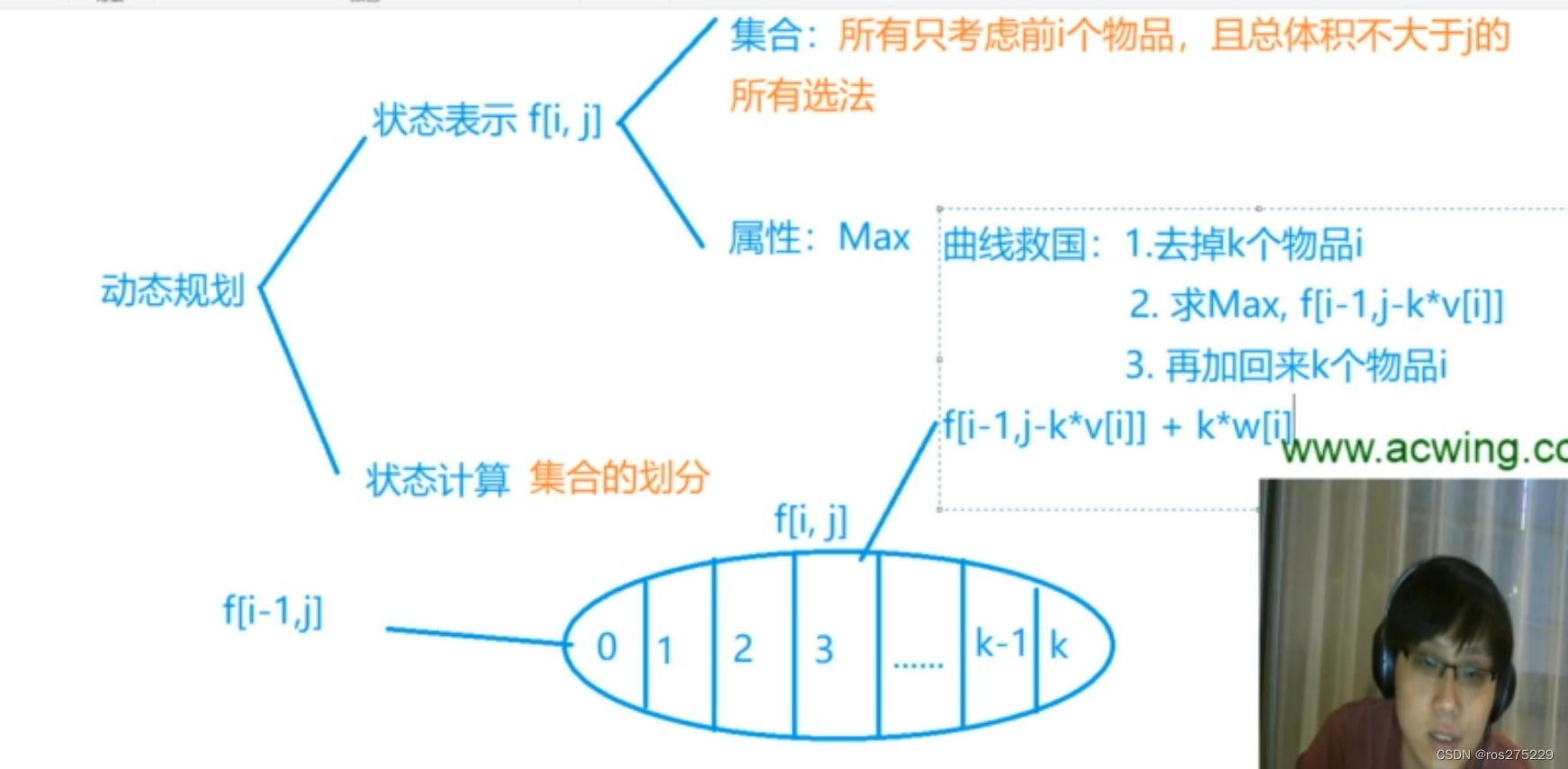
所以状态转移方程式 :

f(i , j) = f( i-1,j-v[i]*k) + w[i] * k

然后根据思路可以模拟出以下的朴素代码 (会超时):

代码(朴素) :

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1005;
int n,m;
int v[N],w[N];
int f[N][N];
​
int main(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k*v[i]<=j;k++){f[i][j] = max(f[i][j] , f[i-1][j-v[i]*k]+w[i]*k);}}}cout << f[n][m] << endl;return 0;
}

代码(优化) :

上面代码有可能会超时( O(n^3) )

优化思路 :

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w ,  f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max(            f[i-1,j-v]   ,  f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
由上两式，可得出如下递推关系： f[i][j]=max(f[i,j-v]+w , f[i-1][j])

然后根据 :

f[i][j] = max(f[i][j-v]+w,f[i-1][j]);

核心循环代码可以优化为 :

for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++)
{f[i][j] = f[i-1][j];if(j-v[i]>=0)f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
}

然后整个代码可以表示为:

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1005;
int n,m;
int v[N],w[N];
int f[N][N];
​
int main(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j] = f[i-1][j];if(j>=v[i]) f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);}}cout << f[n][m] << endl;return 0;
}

代码(一维优化) :

看前一步优化完的代码，先于01背包进行比较 :

f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);//01背包
​
f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包问题

所以相同的进行一维优化 :

 for(int i = 1 ; i<=n ;i++)for(int j = v[i] ; j<=m ;j++)//注意了，这里的j是从小到大枚举，和01背包不一样{f[j] = max(f[j],f[j-v[i]]+w[i]);}

优化完的整体代码 :

#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{int n,m;cin>>n>>m;for(int i = 1 ; i <= n ;i ++){cin>>v[i]>>w[i];}
​for(int i = 1 ; i<=n ;i++)for(int j = v[i] ; j<=m ;j++){f[j] = max(f[j],f[j-v[i]]+w[i]);}cout<<f[m]<<endl;
}

多重背包问题

题目链接 :

4. 多重背包问题 I - AcWing题库

题面 :

思考 :

dp :

状态表示 :

  • 集合 : 说有只从前i个物品中选，总体积不超过j的选法 , 表示成f(i,j)

  • 属性 : max

状态计算 :

  • f(i,j)的集合划分 : 根据第i个物品选多少个，最多选s[i]个，可划分为s[i]+1个集合；

  • 那么就可以确定状态转移方程式了:

    f[i][j] = max(f[i][j] , f[i-1][j-v[i]*k]+w[i]*k);
k = 0,1,2...s[i];

代码 (朴素):

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 105;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k<=s[i]&&k*v[i]<=j;k++){f[i][j] = max(f[i][j] , f[i-1][j-v[i]*k]+w[i]*k);}}}cout << f[n][m] << endl;return 0;
}

多重背包问题II

链接 :

  • 5. 多重背包问题 II - AcWing题库

  • Problem - 2844

思路 :

其它均与上一题相同，不过数据范围扩大了，会超时，那么就要考虑优化的问题;

优化 (这里采用二进制优化的方法) :

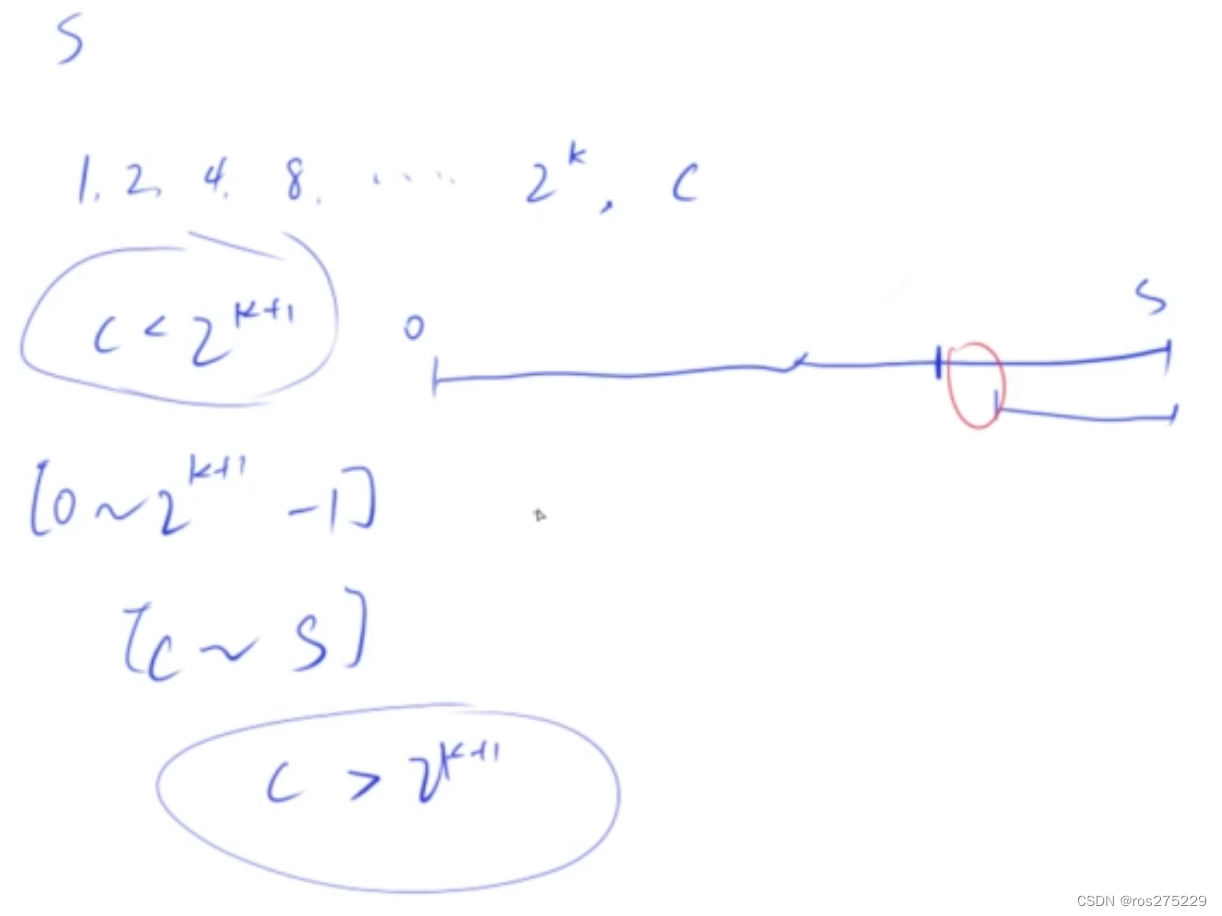
假定给出第i组的物品数量为s[i],也就是s,那么s可以表示为,1,2,4,8,... 2^k,c的和；

由1,2,4,8,... 2^k,c组合可以表示任意[1,s]之间的数；一个log(s)个

例如200可以根据上式表示为 :

1 2 4 8 16 32 64 63

这样分之后，也就是对这每一组数据的分类形成的集合做一个01背包问题，可以把朴素代码的时间复杂度O(N * V * S) 优化为 O(N * V * log(S));

可能这会理解不了，请看详细的二进制优化详解 : 背包问题的二进制优化_二进制优化很神奇_桐小目的博客-CSDN博客

代码(二进制优化) :

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 25000;
int n,m;
int v[N],w[N],s[N];
int f[N];
int main(){cin>>n>>m;int cnt = 0;for(int i=1;i<=n;i++){int a,b,s;cin>>a>>b>>s;int k = 1;while(k<=s){cnt++;v[cnt] = a * k;w[cnt] = b * k;s -= k;k *= 2;}if(s>0){cnt ++;v[cnt] = a * s;w[cnt] = b * s;}}n = cnt;for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--){f[j] = max(f[j],f[j-v[i]]+w[i]);}cout << f[m] << endl;return 0;
}

分组背包问题

题目链接 :

9. 分组背包问题 - AcWing题库

思考 :

  • 集合表示 : f(i,j) 还是 表示 只从前i组物品中选，且总体积不大于j的所有方案数;

  • 属性 : max

  • 状态计算 : 思想与前几题相类似，f(i,j)划分为不从第i组中选物品和从第i组中选第k个物品两种情况；

  • 状态转移方程式 :

    f[i][j] = max(f[i-1][j] , f[i-1][j-v[i,k]]+w[i][k]);

那么就可以轻松得到以下代码 :

代码 (朴素):

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 105;
int n,m;
int v[N][N],w[N][N],s[N];
int f[N][N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=0;j<s[i];j++)cin>>v[i][j]>>w[i][j];}for(int i=1;i<=n;i++)for(int j=0;j<=m;j++){f[i][j] = f[i-1][j];for(int k=0;k<s[i];k++){if(j>=v[i][k])f[i][j] = max(f[i][j] , f[i-1][j-v[i][k]]+w[i][k]);}}cout << f[n][m] << endl;return 0;
}

代码(一维优化) :

因为只用到了第i-1列，所以可以仿照01背包的套路逆向枚举体积

#include<bits/stdc++.h>
using namespace std;
​
const int N=110;
int f[N];
int v[N][N],w[N][N],s[N];
int n,m,k;
​
int main(){cin>>n>>m;for(int i=0;i<n;i++){cin>>s[i];for(int j=0;j<s[i];j++){cin>>v[i][j]>>w[i][j];}}
​for(int i=0;i<n;i++){for(int j=m;j>=0;j--){for(int k=0;k<s[i];k++){    //for(int k=s[i];k>=1;k--)也可以if(j>=v[i][k])     f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);  }}}cout<<f[m]<<endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/80208.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

软件测试常用的功能测试方法

软件测试常用的功能测试方法

功能测试 功能测试就是对产品的各功能进行验证&#xff0c;根据功能测试用例&#xff0c;逐项测试&#xff0c;检查产品是否达到用户要求的功能。针对Web系统的常用测试方法如下&#xff1a; 1. 页面链接检查&#xff1a;每一个链接是否都有对应的页面&#xff0c;并且页面之…
阅读更多...
如何判断linux 文件(或lib)是由uclibc还是glibc编译出来的？

如何判断linux 文件(或lib)是由uclibc还是glibc编译出来的？

工作中使用的编译环境有2套编译器&#xff0c;一个是glibc&#xff0c;一个是uclibc。 有些项目使用的glibc编译的lib&#xff0c;和使用uclibc编译的工程&#xff0c;在一起就会出现reference的编译错误如下&#xff1a; 那和如何来判断一个文件是由哪个编译器编译的呢&#…
阅读更多...
软件工程评级B-，有大量调剂名额。北京联合大学考情分析

软件工程评级B-，有大量调剂名额。北京联合大学考情分析

北京联合大学(B-) 考研难度&#xff08;☆&#xff09; 内容&#xff1a;23考情概况&#xff08;拟录取和复试分析&#xff09;、院校概况、23专业目录、23复试详情、各专业考情分析、各科目考情分析。 正文1239字&#xff0c;预计阅读&#xff1a;3分钟 2023考情概况 北京…
阅读更多...
进程,线程,并发相关入门

进程,线程,并发相关入门

进程与线程的简单理解 进程是一个独立的执行单元&#xff0c;它拥有自己的内存空间、文件句柄和系统资源.进程是操作系统层面的,每个应用运行就是一个进程.进程之间通常是隔离的&#xff0c;它们不能直接访问对方的内存空间&#xff0c;必须通过进程间通信&#xff08;IPC&…
阅读更多...
详细解释HiveSQL执行计划

详细解释HiveSQL执行计划

一、前言 Hive SQL的执行计划描述SQL实际执行的整体轮廓&#xff0c;通过执行计划能了解SQL程序在转换成相应计算引擎的执行逻辑&#xff0c;掌握了执行逻辑也就能更好地把握程序出现的瓶颈点&#xff0c;从而能够实现更有针对性的优化。此外还能帮助开发者识别看似等价的SQL其…
阅读更多...
前端面试话术集锦第 12 篇：高频考点（Vue常考基础知识点）

前端面试话术集锦第 12 篇：高频考点（Vue常考基础知识点）

这是记录前端面试的话术集锦第十二篇博文——高频考点（Vue常考基础知识点），我会不断更新该博文。❗❗❗ 这一章节我们将来学习Vue的一些经常考到的基础知识点。 1. 生命周期钩子函数 在beforeCreate钩子函数调用的时候，是获取不到props或者data中的数据的，因为这些数据的…
阅读更多...
log4j2漏洞复现

log4j2漏洞复现

log4j2漏洞复现 漏洞原理 log4j2框架下的lookup查询服务提供了{}字段解析功能&#xff0c;传进去的值会被直接解析。例如${sys:java.version}会被替换为对应的java版本。这样如果不对lookup的出栈进行限制&#xff0c;就有可能让查询指向任何服务&#xff08;可能是攻击者部署…
阅读更多...
MC-4/11/01/400 ELAU 软件允许用户完全访问相机设置

MC-4/11/01/400 ELAU 软件允许用户完全访问相机设置

MC-4/11/01/400 ELAU 软件允许用户完全访问相机设置 一个完整的Sentinel模具保护解决方案包括一到四台冲击式摄像机、专用红外LED照明和镜头、Sentinel软件以及所有与模压机连接的必要互连组件。摄像机支架基于磁性&#xff0c;可快速、安全、灵活地部署。此外&#xff0c;一个…
阅读更多...
部署ik分词器

部署ik分词器

部署ik分词器 案例版本&#xff1a;elasticsearch-analysis-ik-8.6.2 ​ ES默认自带的分词器对中文处理不够友好&#xff0c;创建倒排索引时可能达不到我们想要的结果&#xff0c;然而IK分词器能够很好的支持中文分词 ​ 因为是集群部署&#xff0c;所以每台服务器中的ES都需…
阅读更多...
unity 使用Photon进行网络同步

unity 使用Photon进行网络同步

Pun使用教程 第一步&#xff1a;请确保使用的 Unity 版本等于或高于 2017.4&#xff08;不建议使用测试版&#xff09;创建一个新项目。 第二步&#xff1a;打开资源商店并找到 PUN 2 资源并下载/安装它。 导入所有资源后&#xff0c;让 Unity 重新编译。 第三步&#xf…
阅读更多...
Python中Mock和Patch的区别

Python中Mock和Patch的区别

前言&#xff1a; 嗨喽~大家好呀&#xff0c;这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 在测试并行开发&#xff08;TPD&#xff09;中&#xff0c;代码开发是第一位的。 尽管如此&#xff0c;我们还是要写出开发的测试&#xff0c…
阅读更多...
解决SpringMVC在JSP页面取不到ModelAndView中数据

解决SpringMVC在JSP页面取不到ModelAndView中数据

版权声明 本文原创作者&#xff1a;谷哥的小弟作者博客地址&#xff1a;http://blog.csdn.net/lfdfhl 问题描述 ModelAndView携带数据跳转到指定JSP页面后在该页面通过EL表达式取不到原本存放在ModelAndView中的数据。 问题原因 在IDEA中创建Maven工程时web.xml中默认的约束…
阅读更多...
医院如何实现安全又稳定的跨网文件数据交换呢？

医院如何实现安全又稳定的跨网文件数据交换呢？

随着医疗信息化的发展&#xff0c;医院之间需要频繁地进行文件数据交换&#xff0c;以实现诊疗、科研、管理等方面的协同和共享。然而&#xff0c;由于医院网络环境的复杂性和敏感性&#xff0c;跨网文件数据交换面临着安全性和稳定性的双重挑战。如何在保证文件数据不被泄露、…
阅读更多...
八、硬改之设备画像

八、硬改之设备画像

系列文章目录 第一章 安卓aosp源码编译环境搭建 第二章 手机硬件参数介绍和校验算法 第三章 修改安卓aosp代码更改硬件参数 第四章 编译定制rom并刷机实现硬改(一) 第五章 编译定制rom并刷机实现硬改(二) 第六章 不root不magisk不xposed lsposed frida原生修改定位 第七章 安卓…
阅读更多...
【leetcode 力扣刷题】栈和队列的基础知识 + 栈的经典应用—匹配

【leetcode 力扣刷题】栈和队列的基础知识 + 栈的经典应用—匹配

栈和队列的基础知识 栈的经典应用—匹配 栈和队列基础知识232. 用栈实现队列225. 用队列实现栈 20. 有效的括号1047. 删除字符串中的所有相邻重复项 栈和队列基础知识 数据结构课程介绍线性结构的时候&#xff0c;介绍有线性表、链表、栈和队列。线性表&#xff0c;比如array…
阅读更多...
【k8s】kube-proxy 工作模式

【k8s】kube-proxy 工作模式

文章目录 Userspace模式&#xff1a;iptables模式&#xff1a;负载均衡&#xff08;Load Balancing&#xff09; LB轮询&#xff08;Round Robin&#xff09;&#xff1a;SessionAffinity&#xff1a;最少连接&#xff08;Least Connection&#xff09;&#xff1a;IP哈希&…
阅读更多...
所有字母异位词

所有字母异位词

class Solution { public:vector<int> findAnagrams(string s, string p) {std::vector<int> idxs;// 先获取p的hash串std::string dstr getHash(p);for (int i 0; i<s.length(); i) {// 使用滑动窗口&#xff0c;每次截取p的长度串并hashstd::string sub_str…
阅读更多...
Acwing 828. 模拟栈

Acwing 828. 模拟栈

Acwing 828. 模拟栈 题目要求思路讲解代码展示 题目要求 思路讲解 栈&#xff1a;先进后出 队列&#xff1a;先进先出 代码展示 #include <iostream>using namespace std;const int N 100010;int m; int stk[N], tt;int main() {cin >> m;while (m -- ){string o…
阅读更多...
企业级数据仓库-数仓实战

企业级数据仓库-数仓实战

数仓实战 安装包大小 安装清单 环境搭建 一、环境搭建01&#xff08;机器准备&#xff09; 准备好三台虚拟机&#xff0c;并进行修改hostname、在hosts文件增加ip地址和主机名映射 。 1、设置每个虚拟机的hostname vi /etc/sysconfig/network 修改HOSTNAMEnode02修改hostna…
阅读更多...
将阿里云盘挂载到本地磁盘-CloudDrive工具使用教程

将阿里云盘挂载到本地磁盘-CloudDrive工具使用教程

CloudDrive是什么&#xff1f; 支持将115、沃家云盘、天翼云盘、阿里云盘、WebDAV挂载到本地并创建本地磁盘。 CloudDrive是一个全方位的云存储管理平台&#xff0c;旨在无缝集成多个云存储服务&#xff0c;将它们统一整合到一个界面中。 使用CloudDrive&#xff0c;您可以轻松…
阅读更多...
最新文章

Copyright @ 2022~2023