刷题之动态规划

前言

大家好，我是jiantaoyab，开始刷动态规划的题目了，要特别注意初始化的时候给什么值。

动态规划5个步骤

状态表示：dp数组中每一个下标对应值的含义是什么->dp[i]表示什么
状态转移方程： dp[i] 等于什么
1 和 2 是动态规划的核心步骤，第三步是初始化，保证填表的时候不越界
填表顺序：为了保证填写当前状态的时候，所需要的状态已经计算过
返回值

第 N 个泰波那契数

题目分析

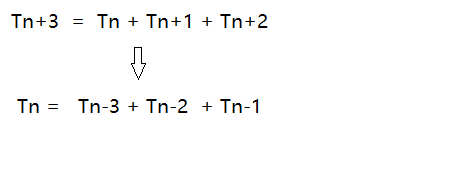
我们用动态规划来解决

dp[i] : 表示第i个泰波那契数
dp[i] = dp[i - 3] + dp[i - 2] + dp [i - 1]
初始化： dp[0] = 0; dp[1] = 1 ; dp[2] = 1;
填表顺序：从左道右
返回值：dp[n]

代码

class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;int dp[1000] = {0};dp[0] = 0, dp[1] = 1, dp[2] = 1;for(int i = 3; i <= n; i++){dp[i] = dp[i-3] + dp[i-2] + dp[i-1];}return dp[n];}
};

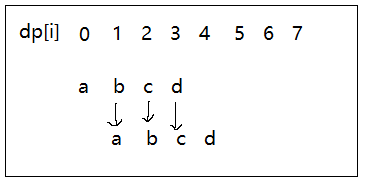
优化一下，可以看到只需要三个变量也能完成这个操作。

class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;int a = 0, b = 1, c = 1, d = 0;for(int i = 3; i <= n; i++){d = a + b + c;a = b;b = c;c = d;}return d;}
};

三步问题

题目分析

dp[i] :表示去到当前台阶有几种方法
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
初始化 dp[1] = 1; dp[2] = 2; dp[3] = 4;
填表顺序从左到右
返回值 d[n]

代码

class Solution {
public:int waysToStep(int n) {vector<int>dp(n + 1);if(n == 1 || n == 2) return n;if(n == 3) return 4;const int MOD = 1000000007;dp[1] = 1; dp[2] = 2; dp[3] = 4;for(int i = 4; i <= n; i++){dp[i] = ((dp[i-3] + dp[i-2]) % MOD + dp[i-1]) % MOD;}return dp[n];}
};

使用最小花费爬楼梯

题目分析

dp[i]：到达 i位置的最小花费
dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);
初始化：dp[0] = dp[1] = 0;
填表顺序:从左到右
返回值：dp[n]

代码

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n + 1);dp[0] = dp[1] = 0;for(int i = 2; i <= n; i++){dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);}return dp[n];}
};

解码方法

题目分析

dp[i]：是表示是 i 位置为结尾的解码方法总数
dp[i] = dp[i - 1] + dp [i - 2];
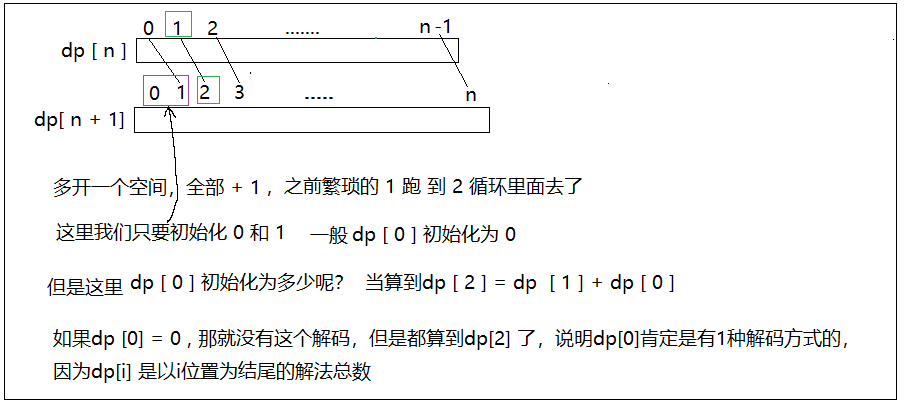
初始化：dp[0] = 0 / 1 dp[1] = 0/ 1/ 2
填表顺序:从左到右
返回值：dp[n - 1]

代码

class Solution {
public:int numDecodings(string s) {int n = s.size();vector<int> dp (n);//初始化dp[0] = s[0] != '0';if(n == 1) return dp[0];if(s[0] != '0' && s[1] != '0') dp[1] += 1;int tmp = (s[0] - '0') * 10 + (s[1] - '0');if(tmp >= 10 && tmp <= 26) dp[1] += 1;//处理剩下的for(int i = 2; i < n; i++){//单独一个字符if(s[i] != '0') dp[i] += dp[i - 1];//2个字符int tmp = (s[i - 1] - '0') * 10 + (s[i] - '0');if(tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];}return dp[n - 1];}
};

优化代码

class Solution {
public:int numDecodings(string s) {int n = s.size();vector<int> dp (n + 1); //初始化dp[0] = 1;dp[1] = s[1 - 1] != '0';  //处理剩下的for(int i = 2; i <= n; i++){//单独一个字符if(s[i - 1] != '0') dp[i] += dp[i - 1];//2个字符int tmp = (s[i - 2] - '0') * 10 + (s[i - 1] - '0');if(tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];}return dp[n];}
};

不同路径

题目分析

dp[i] [j]：走到 i,j 位置有多少种方式
dp[i] [j] = dp[i] [j - 1] + dp[i - 1] [j];
初始化：新增加一列和一行
填表顺序:从上到下，左到右填表
返回值：dp[m] [n]

代码

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1));//初始化dp[0][1] = 1;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}}return dp[m][n];}
};

不同路径 II

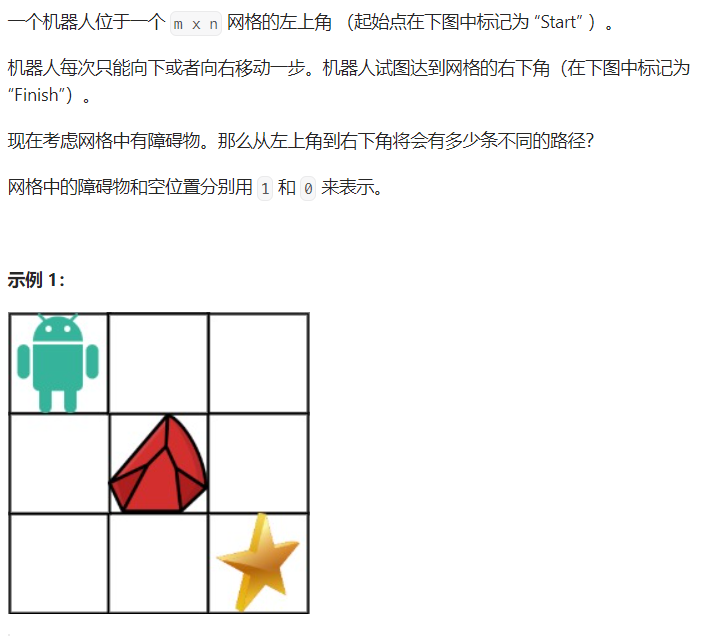
题目分析

dp [i] [j] : 到达i,j这个位置有多少种方法
dp [i] [j] = dp[i - 1] [j] + dp [i] [j - 1]
初始化：dp[1] [0] = 1;
填表顺序：从上到下，从左到右
返回值： dp[m] [n]

代码

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size(), n = obstacleGrid[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));//初始化dp[1][0] = 1;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(obstacleGrid[i - 1][j - 1] != 1)dp[i][j] = dp[i - 1][j] + dp[i][j -1];}}return dp[m][n];} 
};

珠宝的最高价值

题目分析

dp [i] [j] : 到达i,j这个位置的最高价值
dp [i] [j] =max(dp[i-1] [j], dp[i] [j-1]) + frame[i-1] [j-1];
初始化：默认都是0不用初始化
填表顺序：从上到下，从左到右
返回值： dp[m] [n]

代码

class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {int m = frame.size(), n = frame[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++){           dp[i][j] =  max(dp[i-1][j], dp[i][j-1]) + frame[i-1][j-1];}return dp[m][n];}
};

下降路径最小和

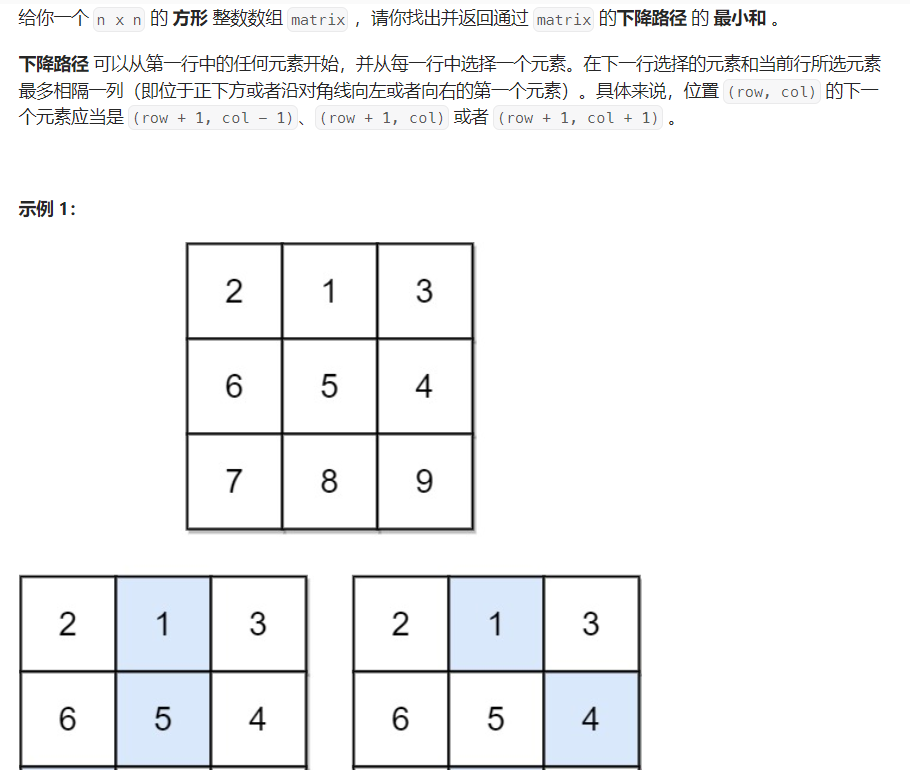
题目分析

dp[i] [j] : 到达i,j位置的最小下路径
dp[i] [j] : min(dp[i+1] [j-1], dp[i+1] [j+1], dp[i+1] [j]) + matrix[i-1] [j - 1]
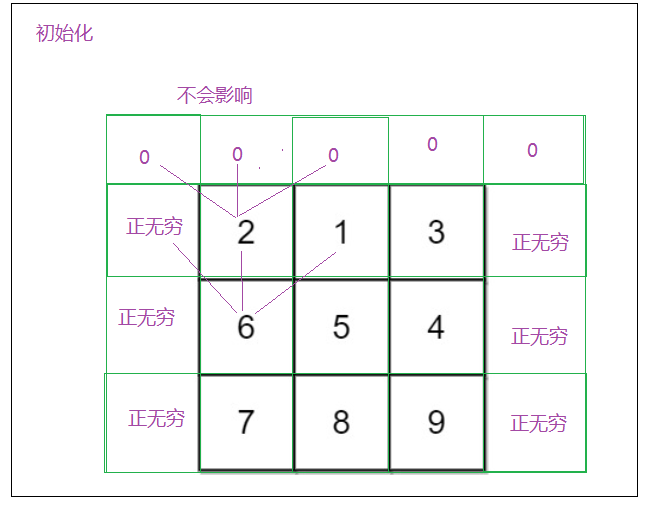
初始化：多给1行和2列
填表顺序：从上到下，从左到右
返回值：最后一行的最小值

代码

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));for(int j = 0; j < n + 2; j++) dp[0][j] = 0;for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){dp[i][j] = min(min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]) + matrix[i-1][j-1];}}      //返回值int ret = INT_MAX;for(int j = 1; j <= n; j++){ret = min(ret, dp[n][j]);}return ret;}
};

最小路径和

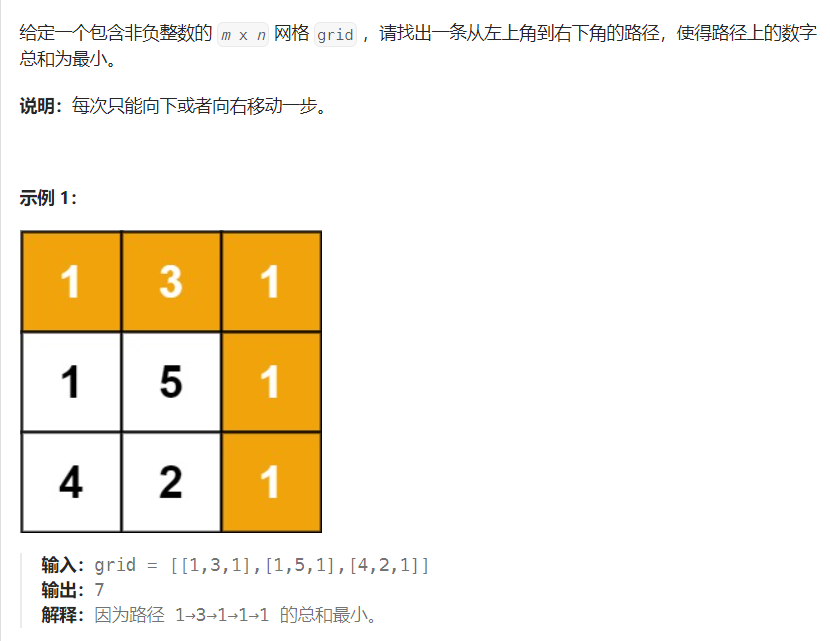
代码

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[1][0] = dp[0][1] = 0; for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++){dp[i][j] = min(dp[i][j - 1], dp[i - 1][j]) + grid[i - 1][j - 1];}return dp[m][n];}
};

地下城游戏（反着来）

题目分析

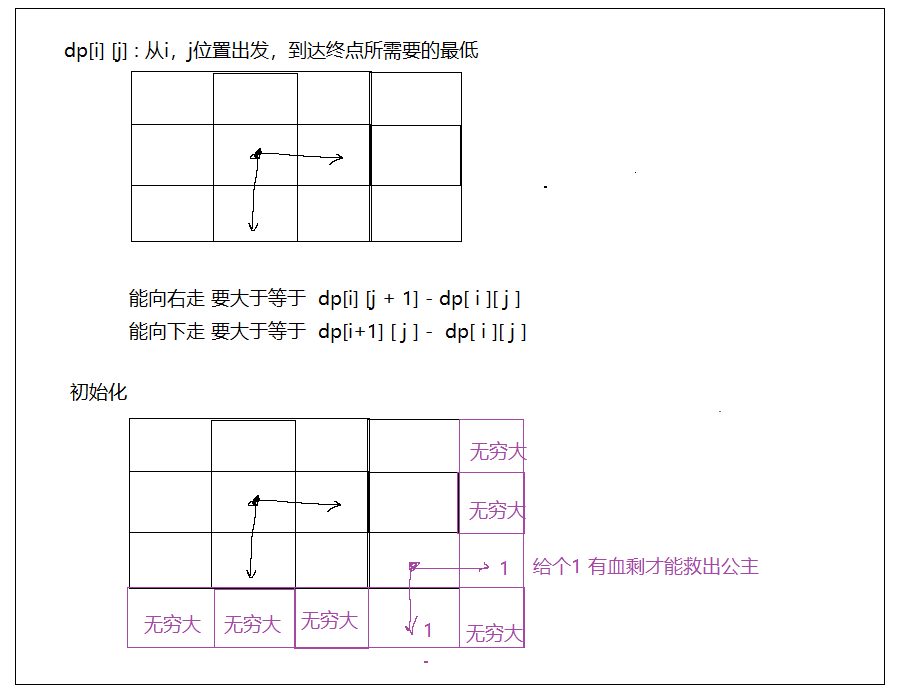
dp[i] [j] : 从i，j位置出发，到达终点所需要的最低
dp[i] [j] = min(dp[i] [j + 1], dp[i + 1] [j]) - dungeon[i] [j];
初始化 dp[m +1] [n -1] = dp [m - 1] [n + 1] = 1;
填表顺序：从下到上，从右到左
返回值： dp[0] [0]

代码

class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m = dungeon.size(), n = dungeon[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));//初始化dp[m][n -1] = dp [m - 1][n] = 1;for(int i = m - 1; i >= 0; i--)for(int j = n - 1; j >= 0; j--){dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j];dp[i][j] = max(1, dp[i][j]); //如果血包很大，会出现负数，这里取1就是最低血}return dp[0][0];}
};