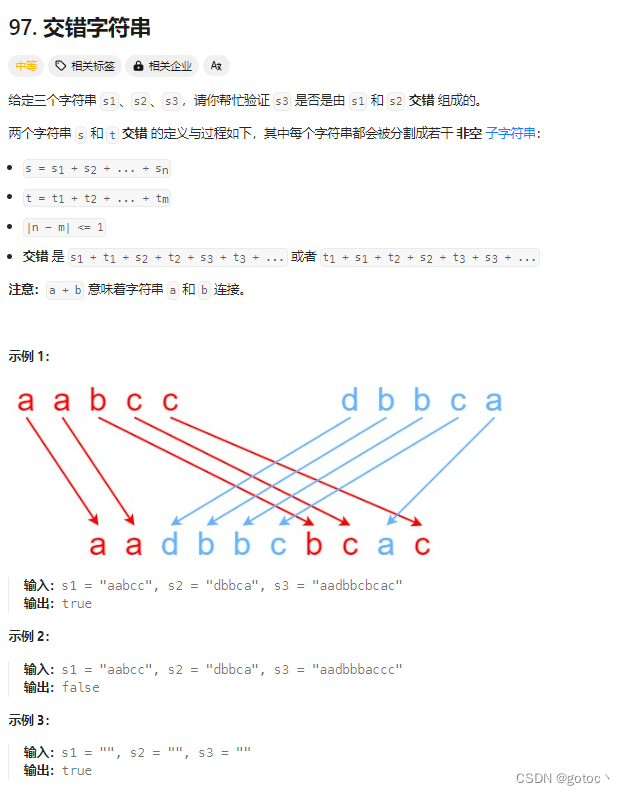
思路分析：

1. 动态规划数组定义：

   • dp[i][j] 表示：使用字符串 s1 的前 i 个字符和字符串 s2 的前 j 个字符，能否构成字符串 s3 的前 i + j 个字符的交错组合。

2. 初始化：

   • dp[0][0] 初始化为 1，表示空串是 s1 和 s2 的交错组成。
   • 初始化第一行和第一列，检查 s1 和 s2 的前缀是否与 s3 的对应前缀相等，若相等则标记为 1。

3. 递推关系：

   • dp[i][j] 的值取决于 s1[i-1]、s2[j-1] 与 s3[i+j-1] 是否匹配，以及之前的状态：
     • 如果 s3[i+j-1] == s1[i-1] 且 dp[i-1][j] == 1，表示当前字符匹配且前缀也能交错组成，标记 dp[i][j] = 1。
     • 如果 s3[i+j-1] == s2[j-1] 且 dp[i][j-1] == 1，表示当前字符匹配且前缀也能交错组成，标记 dp[i][j] = 1。

4. 最终结果：

   • dp[len1][len2] 的值将告诉我们整个字符串 s3 是否可以由 s1 和 s2 交错组成。

5. 返回结果：

   • 返回 dp[len1][len2]。

class Solution {
public:// 判断字符串 s3 是否是由字符串 s1 和 s2 交错组成的bool isInterleave(string s1, string s2, string s3) {// 获取字符串 s1、s2、s3 的长度int len1 = s1.length();int len2 = s2.length();int len3 = s3.length();// 如果 s1 和 s2 的长度之和不等于 s3 的长度，直接返回 falseif (len1 + len2 != len3)return false;// 处理特殊情况：当 s1 为空时，判断 s2 和 s3 是否相等；当 s2 为空时，判断 s1 和 s3 是否相等if (len1 == 0 && s2 == s3)return true;if (len2 == 0 && s1 == s3)return true;// 创建二维数组 dp，用于记录 s1 和 s2 是否能够交错组成 s3 的子串vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1, 0));// 初始化 dp[0][0] 为 1，表示空串是 s1 和 s2 的交错组成dp[0][0] = 1;// 初始化第一行，如果 s1 的前缀和 s3 相等，标记 dp[i][0] 为 1for (int i = 1; i <= len1; ++i) {if (s1[i - 1] == s3[i - 1])dp[i][0] = 1;elsebreak;}// 初始化第一列，如果 s2 的前缀和 s3 相等，标记 dp[0][j] 为 1for (int i = 1; i <= len2; ++i) {if (s2[i - 1] == s3[i - 1])dp[0][i] = 1;elsebreak;}// 动态规划，填充 dp 数组for (int i = 1; i <= len1; ++i) {for (int j = 1; j <= len2; ++j) {// 如果 s3 的当前字符等于 s1 的当前字符，并且 s1 的前缀也能够组成 s3 的前缀，则标记 dp[i][j] 为 1if (s3[i + j - 1] == s1[i - 1] && dp[i - 1][j])dp[i][j] = 1;// 如果 s3 的当前字符等于 s2 的当前字符，并且 s2 的前缀也能够组成 s3 的前缀，则标记 dp[i][j] 为 1if (s3[i + j - 1] == s2[j - 1] && dp[i][j - 1])dp[i][j] = 1;}}// 返回 dp 数组右下角的值，表示整个 s3 是否由 s1 和 s2 交错组成return dp[len1][len2];}
};

这个还是很抽象难理解，这里举个例子：
 

假设我们有两个字符串 s1 = "abc"，s2 = "def"，以及 s3 = "adbcef"。我们想要判断是否可以通过交错组合 s1 和 s2 得到 s3。

我们可以用一个二维数组 dp[i][j] 来表示 s1 的前 i 个字符和 s2 的前 j 个字符是否可以组成 s3 的前 i+j 个字符。

1. 初始化：

   • dp[0][0] 初始化为 1，因为空串是任何字符串的子串，所以空串可以由 s1 和 s2 交错组成。
   • 初始化第一行和第一列，检查 s1 和 s2 的前缀是否能够交错组成 s3 的前缀

   dp array:
  d e f
 1 0 0 0
a 1 0 0 0
b 0 0 0 0
c 0 0 0 0

2. 递推关系：

   • 我们递推地填充 dp 数组。在这个过程中，如果当前字符匹配，我们要考虑之前的状态是否可行。
   • 对于 dp[i][j]，如果 s3[i+j-1] 与 s1[i-1] 匹配，并且 dp[i-1][j] 为 1，那么 dp[i][j] 也可以为 1。同样，如果 s3[i+j-1] 与 s2[j-1] 匹配，并且 dp[i][j-1] 为 1，那么 dp[i][j] 也可以为 1。

   dp array:
  d e f
 1 0 0 0
a 1 1 1 0
b 0 1 0 0
c 0 0 1 0

3. 最终结果：

   • 最终的 dp[len1][len2] 为 1，表示整个字符串 s3 可以由 s1 和 s2 交错组成。