文章目录
- 🍀引言
- 🍀eta参数的调节
- 🍀sklearn中的梯度下降
🍀引言
承接上篇,这篇主要有两个重点,一个是eta参数的调解;一个是在sklearn中实现梯度下降
在梯度下降算法中,学习率(通常用符号η表示,也称为步长或学习速率)的选择非常重要,因为它直接影响了算法的性能和收敛速度。学习率控制了每次迭代中模型参数更新的幅度。以下是学习率(η)的重要性:
-
收敛速度:学习率决定了模型在每次迭代中移动多远。如果学习率过大,模型可能会在参数空间中来回摇摆,导致不稳定的收敛或甚至发散。如果学习率过小,模型将收敛得很慢,需要更多的迭代次数才能达到最优解。因此,选择合适的学习率可以加速收敛速度。
-
稳定性:过大的学习率可能会导致梯度下降算法不稳定,甚至无法收敛。过小的学习率可以使算法更加稳定,但可能需要更多的迭代次数才能达到最优解。因此,合适的学习率可以在稳定性和收敛速度之间取得平衡。
-
避免局部最小值:选择不同的学习率可能会导致模型陷入不同的局部最小值。通过尝试不同的学习率,您可以更有可能找到全局最小值,而不是被困在局部最小值中。
-
调优:学习率通常需要调优。您可以尝试不同的学习率值,并监视损失函数的收敛情况。通常,您可以使用学习率衰减策略,逐渐降低学习率以改善收敛性能。
-
批量大小:学习率的选择也与批量大小有关。通常,小批量梯度下降(Mini-batch Gradient Descent)使用比大批量梯度下降更大的学习率,因为小批量可以提供更稳定的梯度估计。
总之,学习率是梯度下降算法中的关键超参数之一,它需要仔细选择和调整,以在训练过程中实现最佳性能和收敛性。不同的问题和数据集可能需要不同的学习率,因此在实践中,通常需要进行实验和调优来找到最佳的学习率值。
🍀eta参数的调节
在上代码前我们需要知道,如果eta的值过小会造成什么样的结果
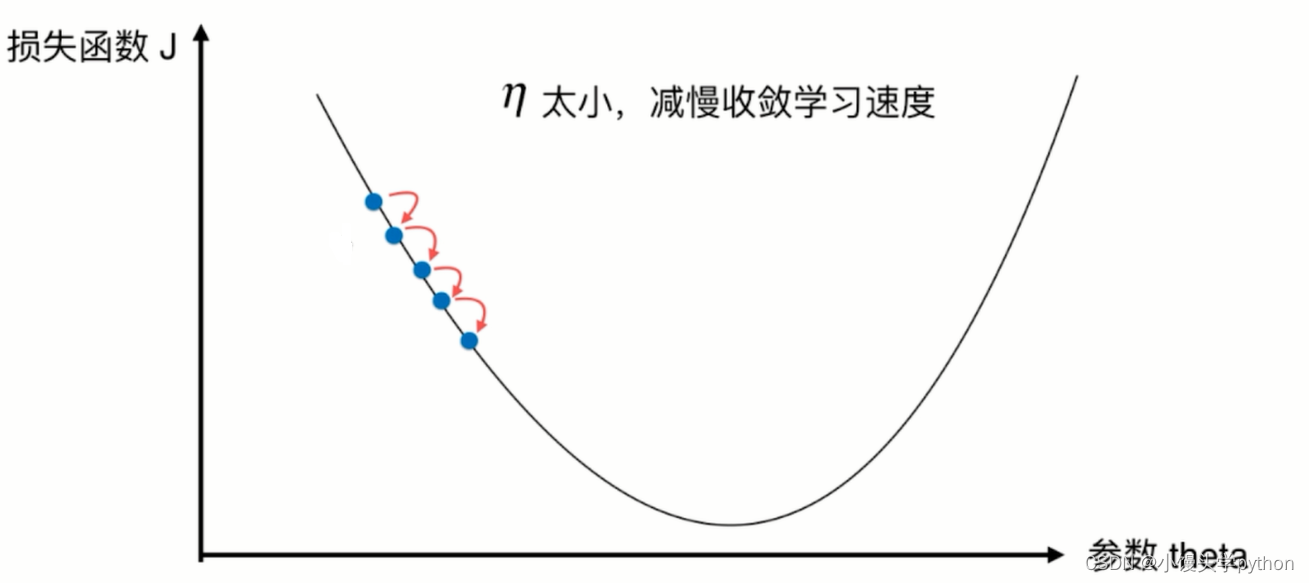
反之如果过大呢
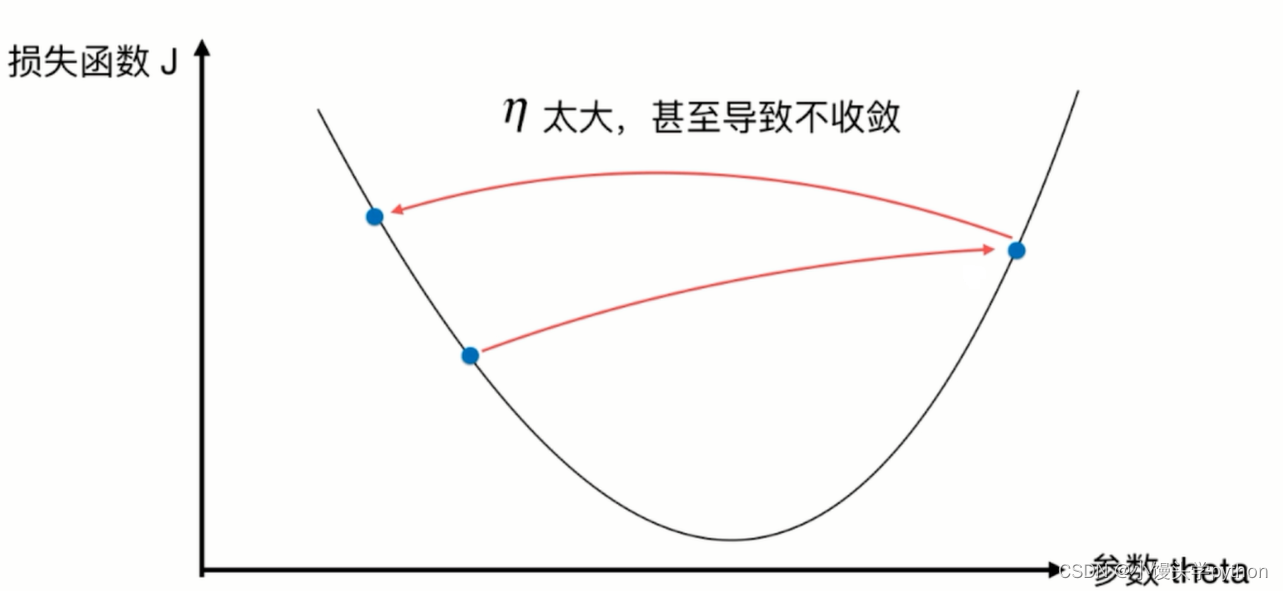
可见,eta过大过小都会影响效率,所以一个合适的eta对于寻找最优有着至关重要的作用
在上篇的学习中我们已经初步完成的代码,这篇我们将其封装一下
首先需要定义两个函数,一个用来返回thera的历史列表,一个则将其绘制出来
def gradient_descent(eta,initial_theta,epsilon = 1e-8):theta = initial_thetatheta_history = [initial_theta]def dj(theta): return 2*(theta-2.5) # 传入theta,求theta点对应的导数def j(theta):return (theta-2.5)**2-1 # 传入theta,获得目标函数的对应值while True:gradient = dj(theta)last_theta = thetatheta = theta-gradient*eta theta_history.append(theta)if np.abs(j(theta)-j(last_theta))<epsilon:breakreturn theta_historydef plot_gradient(theta_history):plt.plot(plt_x,plt_y)plt.plot(theta_history,[(i-2.5)**2-1 for i in theta_history],color='r',marker='+')plt.show()
其实就是上篇代码的整合罢了
之后我们需要进行简单的调参了,这里我们分别采用0.1、0.01、0.9,这三个参数进行调节
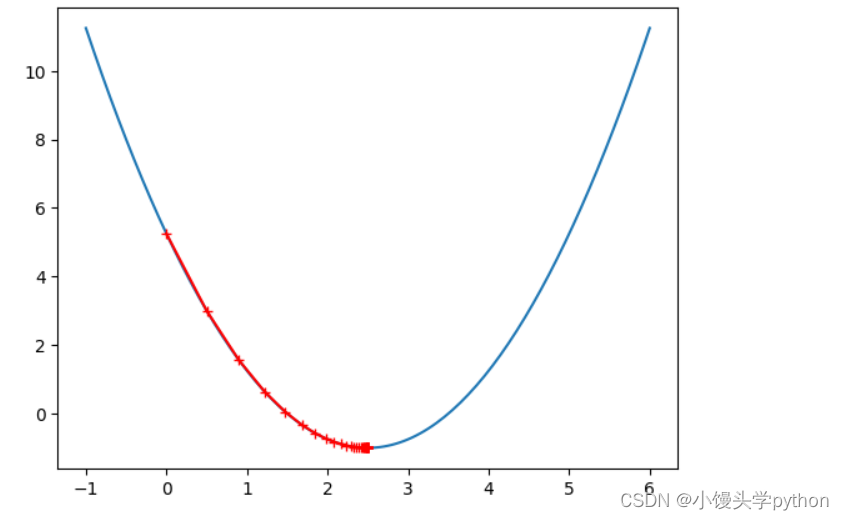
eta = 0.1
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
eta = 0.01
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下

eta = 0.9
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
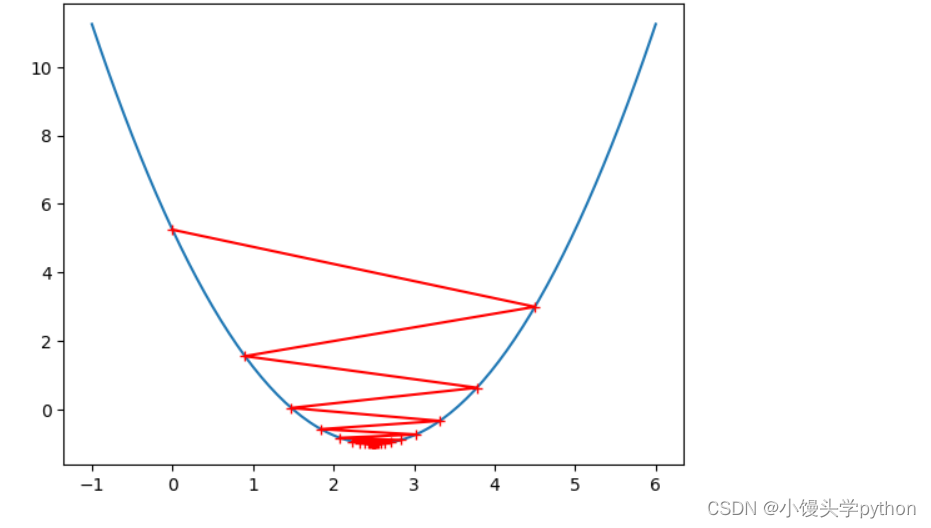
这三张图与之前的提示很像吧,可见调参的重要性
如果我们将eta改为1.0呢,那么会发生什么
eta = 1.0
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
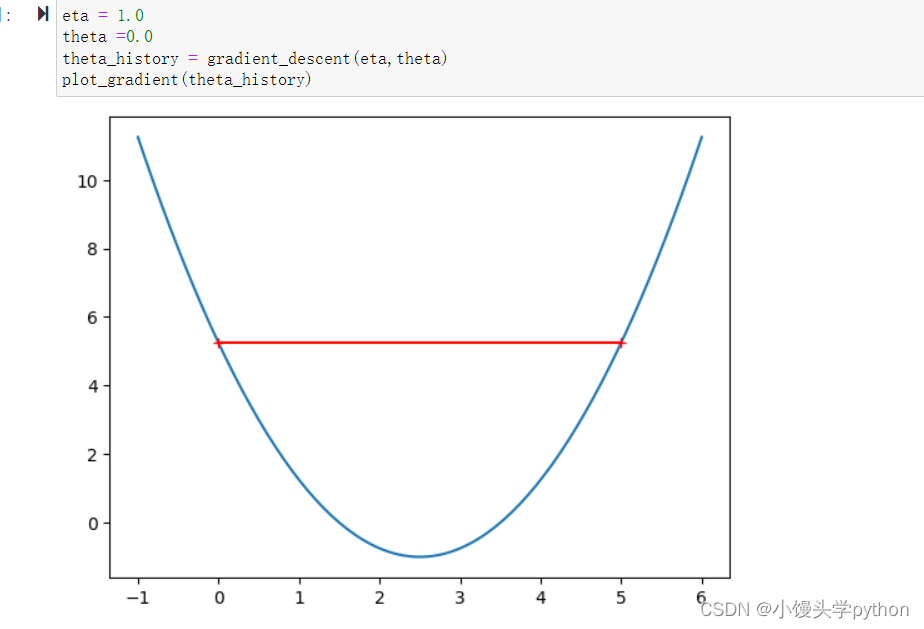
那改为1.1呢
eta = 1.1
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
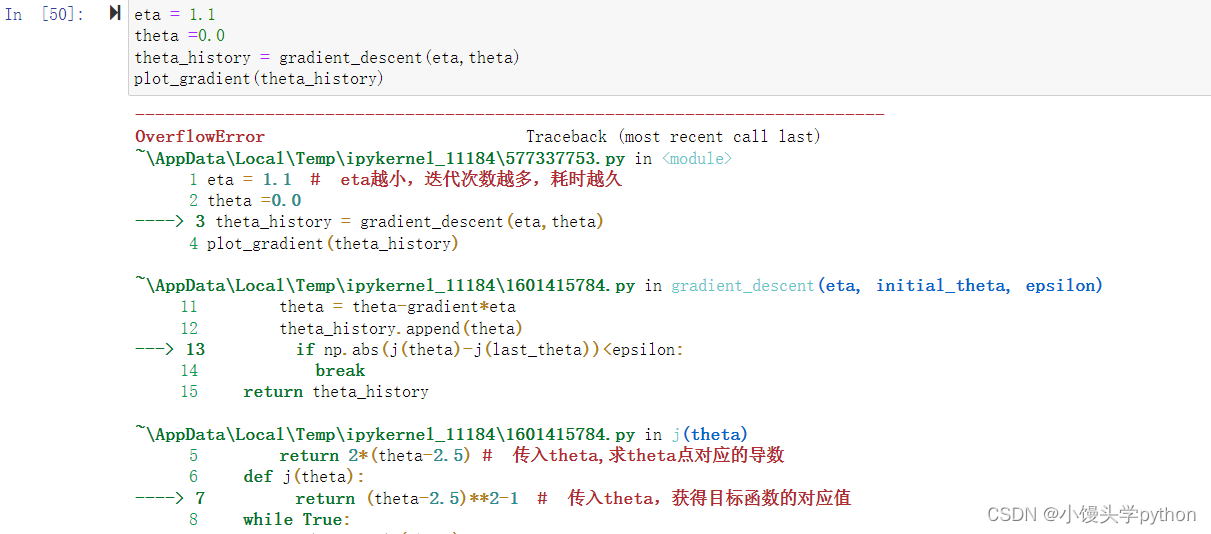
我们从图可以清楚的看到,当eta为1.1的时候是嗷嗷增大的,这种情况我们需要采用异常处理来限制一下,避免报错,处理的方式是限制循环的最大值,且可以在expect中设置inf(正无穷)
def gradient_descent(eta,initial_theta,n_iters=1e3,epsilon = 1e-8):theta = initial_thetatheta_history = [initial_theta]i_iter = 1def dj(theta): try:return 2*(theta-2.5) # 传入theta,求theta点对应的导数except:return float('inf')def j(theta):return (theta-2.5)**2-1 # 传入theta,获得目标函数的对应值while i_iter<=n_iters:gradient = dj(theta)last_theta = thetatheta = theta-gradient*eta theta_history.append(theta)if np.abs(j(theta)-j(last_theta))<epsilon:breaki_iter+=1return theta_historydef plot_gradient(theta_history):plt.plot(plt_x,plt_y)plt.plot(theta_history,[(i-2.5)**2-1 for i in theta_history],color='r',marker='+')plt.show()
注意:inf表示正无穷大
🍀sklearn中的梯度下降
这里我们还是以波士顿房价为例子
首先导入需要的库
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
之后取一部分的数据
boston = load_boston()
X = boston.data
y = boston.target
X = X[y<50]
y = y[y<50]
然后进行数据归一化
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y)
std = StandardScaler()
std.fit(X_train)
X_train_std=std.transform(X_train)
X_test_std=std.transform(X_test)
sgd_reg = SGDRegressor()
sgd_reg.fit(X_train_std,y_train)
最后取得score
sgd_reg.score(X_test_std,y_test)
运行结果如下


挑战与创造都是很痛苦的,但是很充实。

)

——系统基本配置与开关机命令)





k8s实战-高级调度)



框架)



)
利用opencv进行图像几何转换)
