以下是关于下三角矩阵L的行列式一定等于+-1的一些说明
笔者的一些话(写在最前面):
这是一篇小文,是我写的关于求解矩阵行列式的一篇文章中的一部分。之所以把这一段专门提溜出来,是因为这一段相对于原文是可以完全独立的,也是因为我自认为这是原文中很精彩的一段论证。为了便于我自己后续翻阅和查找,也是为了给我CSDN文章里面凑数,这才有了这篇文章。
证明:在LU分解中,下三角矩阵L的行列式一定是.
在证明之前,我这里先补充几条关于行列式的性质:
性质1:对于三角矩阵而言,不论是上三角矩阵还是下三角矩阵,其行列式的值都等于主对角线上元素的乘积。

此处引用Gilbert strang的线性代数教科书《introduction to linear algebra》中,第251页处的一段关于矩阵行列式的相应说明:

截图中第七条性质说:如果矩阵A是一个三角矩阵,则矩阵A的行列式等于其对角线上元素的乘积。
性质2:两个矩阵A,B的积AB的行列式|AB|等于这两个矩阵各自的行列式|A|和|B|的积,即:

性质3:单位矩阵I的行列式为1。
性质4:对矩阵进行行与行之间的交换后,需要改变原矩阵行列式的正负号。

在LU分解中,下三角阵L是高斯消元的逆过程,是多个消元矩阵E的逆矩阵的乘积(形如下图中的矩阵)。

首先,根据上面说的性质1可知,所有消元矩阵E的逆矩阵的行列式等于其对角线上所有元素的乘积。又因为矩阵
对角线上元素都是1,所以,
的行列式一定等于1。此外,根据性质2,L的行列式等于多个
的行列的乘积,所以,L的行列式必然等于1,即:
可是,如果对矩阵A进行高斯消元的过程中,遇到对角线上的元素为0的情况,就需要对矩阵进行行交换,则上式就会包含一些置换矩阵:
这种情况下计算出来的L矩阵可就不一定是标准的下三角矩阵了,比如说下面这个矩阵:

这样一来就需要对L矩阵进行行交换,把他变成标准的下三角矩阵,以确保他的det等于1。而交换的过程需要用置换矩阵P记录下来,使得原来的L,变成PL(这时的L已经是标准的下三角矩阵了)。因为置换矩阵P只不过是对单位矩阵I进行行交换后的结果,因此,综合性质3和性质4可知,置换矩阵P的行列式的值只能是+1或-1。在结合前面得出的L矩阵的行列式一定是1的结论,最终PL的行列式只能是+1或-1。
因此,当我们基于矩阵A的LU分解计算出L的det后(必然是1),如果高斯消元的过程中进行过行交换,还要再根据行交换的次数(置换矩阵P)去调整det的符号。
事实上,在matlab中自带的计算矩阵行列式的det函数就利用了这一点。
按照Matlab的官方说明文档,首先,他在计算矩阵的det时先调了lu分解函数,对矩阵进行分解。
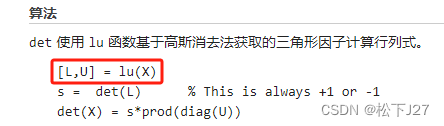
注意,matlab的lu分解函数有很多,只是他在计算行列式时,调用的是[L,U]=lu(A)。
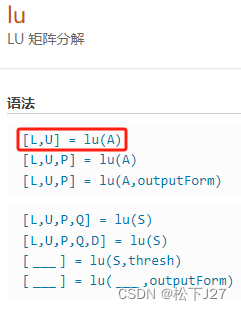
 按照他官方文档的说法,分解后的L矩阵和U矩阵中,L矩阵有被置换过,也就不是标准的三角矩阵。这和我们前面提到的,如果消元时进行过行交换的情况是一致的。
按照他官方文档的说法,分解后的L矩阵和U矩阵中,L矩阵有被置换过,也就不是标准的三角矩阵。这和我们前面提到的,如果消元时进行过行交换的情况是一致的。
然后,对这个“经过置换的下三角矩阵L”进行行交换,并记录交换过程得到:
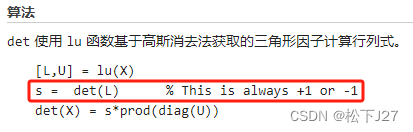
最后一步,求出矩阵U(他一定是一个标准的上三角矩阵)中主对角线上所有元素的乘积,然后和前一步的结果相乘,得到矩阵A的行列式:
例子:


(全文完)
作者 --- 松下J27
参考文献(鸣谢):
1,https://en.wikipedia.org/wiki/Determinant
2,Determinant of a Matrix
3,矩阵行列式 - MATLAB det- MathWorks 中国
4,线性代数 --- LU分解(Gauss消元法的矩阵表示)_矩阵的lu分解-CSDN博客
5,线性代数 --- Gauss消元的部分主元法和完全主元法_部分选主元高斯matlab-CSDN博客

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27










万字)








