1、边缘的特征
先看一张实物图和边缘图
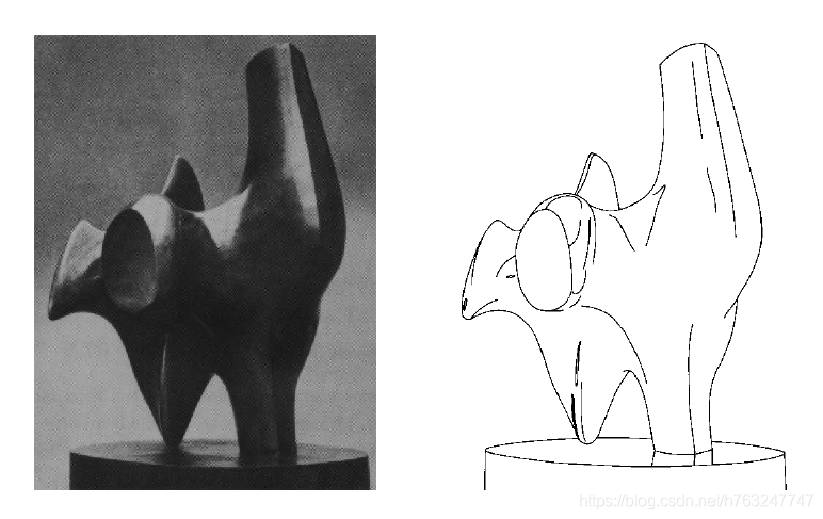
边缘是图片中灰度变化最快的地方。下图清楚地显示了最简单的一种情况。既然找变化最快的地方,可以通过导数来求解边缘
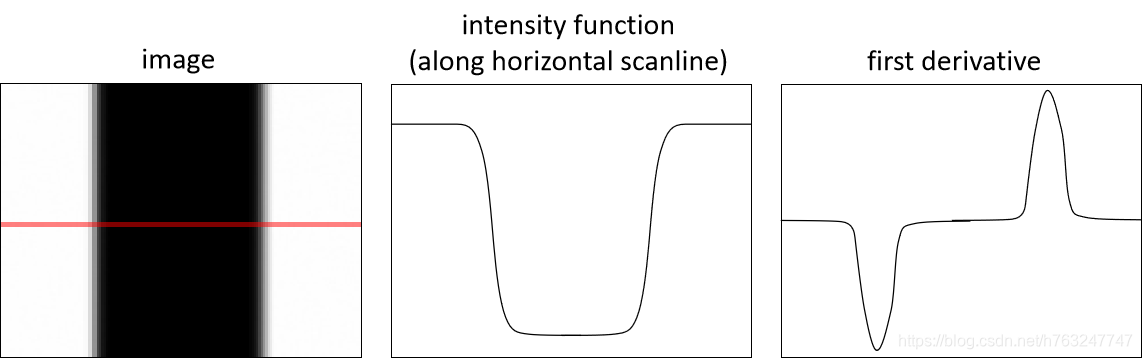
2、图片的导数
一张数字图片F[x,y], 其x方向导数可定义为:


3、图片的梯度
3.1 图片的梯度相关定义

几种常见的图片的梯度

边缘的灰度用图片梯度的幅值表示,

图片梯度的方向:

3.2 图片梯度实例
下图显示了原图,x方向导数的图片,y方向导数的图片,和幅值的图片。

4、图片虚化后的梯度
图片实际上包含有很多噪音,噪音干扰求图片的梯度,如下图所示:

f(x)为红线处的灰度值,对其进行求导,充满干扰。

为了减少噪音的干扰,可使用高斯高斯滤波器过滤掉图片噪音,然后再求图片的梯度。
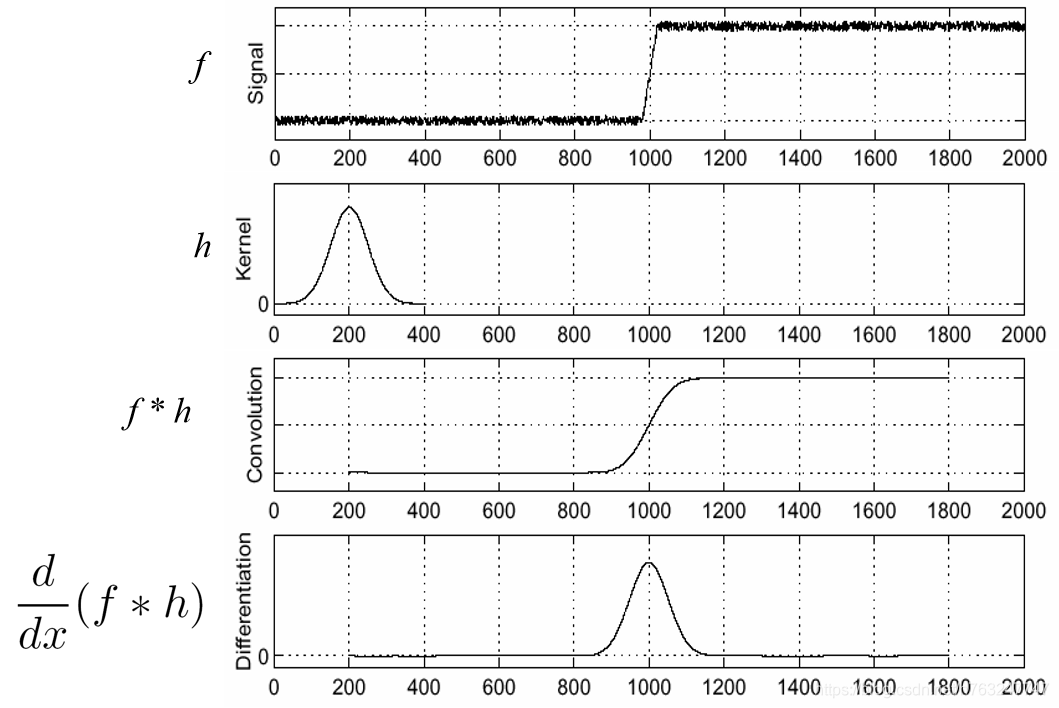
图片的求导可以用卷积运算实现,图片的卷积运算又满足交换律和结合律,所以

下图展示了其计算过程:

5、Sobel 算子
Sobel算子近视表示高斯滤波器的1阶导数,Sobel算子的滤波器如下图所示:
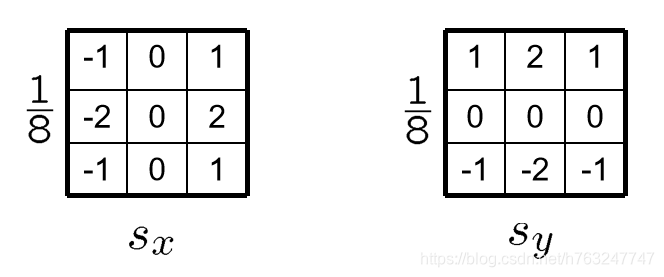
前面的1/8是一个经验值,为了得到合适的梯度的幅值
下方图片展示了Sobel算子的效果:
原图

x方向导数

y方向导数

幅值


6、LoG算子
除了使用高斯滤波器的一阶导数求边缘,还可以使用其二阶导数求边缘,边缘值刚好位于二阶导数的零值。如下图所示:

二维高斯函数的二阶导数如下图所示:
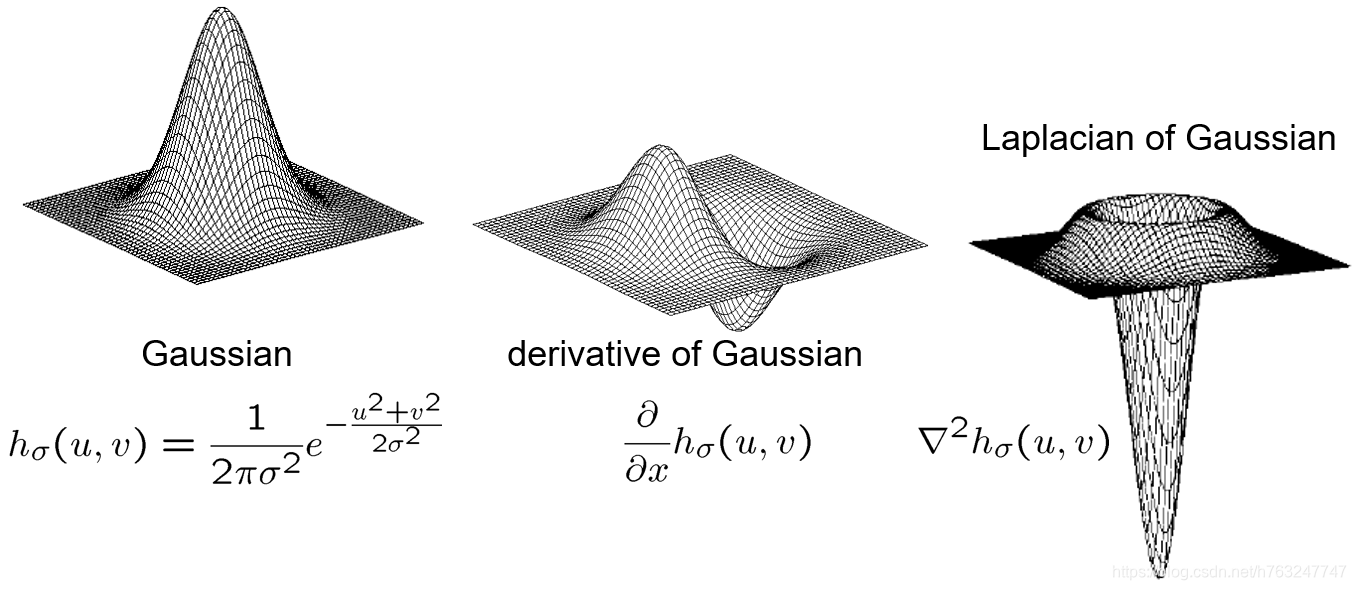
Laplacian 算子

LoG (Laplacian of Gaussian) 算子近似表示高斯滤波器的二阶导数。LoG算子如下图:

7、Canny 边缘检测
7.1Canny 边缘检测的过程
- 用高斯的梯度对图片滤波
- 求出梯度的幅值和方向
- 非极大值抑制(Non-maximum suppression)
- 设定阈值并连接
7.2 非极大值抑制(Non-maximum suppression)
检查一个点沿着该点的梯度方向是否为局部最大值,如果是保留,如果不是抑制.
在Canny 的论文中,梯度方向只有4个,0°,45°,90°,135°,但是实际上,梯度方向有很多种,不仅仅只有四种,
可阅读此博客:Canny算子中的非极大值抑制
非极大值抑制处理之前

非极大值抑制处理之后

7.3 设定阈值并连接
- 设置高低两种阈值
- 梯度幅值大于高阈值的视为强边缘
- 梯度幅值小于低阈值的视为噪声
- 位于高低阈值之间的视为弱边缘
7.4 Canny 边缘检测实例

7.5 Canny边缘检测的问题
不同高斯的 ![]() 值,会影响到边缘检测,如下图所示。
值,会影响到边缘检测,如下图所示。

较大的 能检测到较粗的边缘,较小的
还能检测到较细的边缘。
当使用不同的滤波器时,一节导数的最大值(边缘点)会出现偏移,甚至重合。

8、好的边缘检测算法的标准
- 能够发现所有的边缘
- 不受噪音影响
- 检测到的边缘点离实际点越近越好
- 对于每一个实际的边缘点,算法只返回一个点
)



-汇编基础)

)

)





)



)
)