
来源: 集智俱乐部
作者:陈昊
编辑:邓一雪
导语
因果涌现理论指出,在宏观尺度下观察复杂系统可以减少因果关系中的噪声,从而得到具有更强因果关联的系统。目前该理论已经在有效信息和整合信息的因果度量标准下得到的验证,但其在更多因果度量标准上的普遍性仍需要进一步检验。近日,由有效信息理论提出者Erik Hoel作为通讯作者挂载在ArXiv上的一篇文章使用十二种彼此独立但均有广泛应用的因果度量标准验证了因果涌现理论的普适性。
研究领域:因果涌现,因果度量,信息熵

论文题目:
Causal emergence is widespread across measures of causation
论文地址:
https://arxiv.org/abs/2202.01854
1. 统一因果度量标准是否必要?
在过去几十年的不断探索中,因果——一个曾经只会出现在哲学辩论中的话题,正逐渐被我们放进严谨的数学框架之中。特别的是,对于因果这一主题的讨论并不仅仅局限于单一学科背景,来自心理学、统计学等多个学科的学者都对其数学理论的建设有着自己的贡献[1]。如在神经科学中,科学家就会使用多种度量因果的标准来对实验干预进行处理。然而,正是由于不同背景的研究者们从自身角度出发提出了多种因果度量指标,目前我们还无法找到一种足够客观的标准来描述因果。
针对上述问题,有效信息理论的提出者Erik Hoel教授等人近日发表文章指出:不同学科背景下提出的多种度量标准间存在着数学上的联系,很多情形下这些指标都会有相似的表现。更有趣的是,所有这些标准都可以由一些基本指标导出——原文称之为因果基本式(causal primitives)。为了证明上述观点,文章选择了目前较为主流的十二种因果度量标准,通过指出它们具有相同的基本式,揭示了不同指标对于「什么是强因果,什么是弱因果」有着相同的倾向。基于该发现,因果度量标准的不统一将不再是跨学科交流的壁垒。
为了将注意力集中在因果度量标准本身,我们不妨选择将目光聚焦在因果科学中的一个具体现象——因果涌现(casual emergence)。因果涌现现象是指因果关系在宏观通常会更加强[2]。乍一看该现象似乎有些反直觉:作为微观现象的粗粒化,宏观现象似乎完全被微观所绑定,又怎么会有超出微观的因果关系呢?但事实上,从另一个角度来看,宏观视角下的粗粒化可以降低微观尺度中系统的噪声,因此其较强的因果关系有其可解释性。
在以往的研究中,我们只在很有限的几种度量标准(如有效信息[2]与整合信息[3])下验证了因果涌现现象。由于这些测量标准都基于信息论建立且有着较为相似的基本假设,因果涌现现象的普适性受到了质疑[4-6]。在这篇文章中,作者为因果涌现现象的普遍存在性提供了证据,向我们展现了来自不同领域、具有不同基本假设的因果度量标准下都存在着因果涌现现象。
2. 因果关系与因果基本式的标准描述
为了对各个领域的因果评价标准进行比较,我们首先需要规定一套统一的数学语言:将所有可能发生的事件的集合记为Ω,该空间中存在一些原因事件c∈C和一些结果事件e∈E,其中c可能会导致e的发生,C⊆Ω,E⊆Ω。
由于我们将会在马尔可夫链上对因果进行度量,故可以将空间Ω视作一个状态空间,c和e则为状态。原因与结果可以通过转移概率P(e|c)联系起来,该转移概率表示系统处于c状态的情况下,下一时刻变为e的概率。此外为了对原因事件的反事实(即如果原因事件不发生,系统会如何演进)进行估计,我们还需要将c事件不发生的条件下e发生的概率表示为P(e|C\c),其中C\c表示c的补集。
2.1 充分性与必要性
基于上述规定,我们便可以开始定义一系列的因果基本式。首先对于任何一个原因状态c,我们都可以讨论其对任意结果状态e发生的充分性(sufficiency),即在系统处于原因状态c的情况下结果状态e出现的概率,表示为
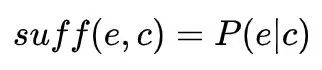
反之,我们还可以考虑任意一个原因状态c对于任意结果状态e发生的必要性(necessity),即系统想要达到结果状态e多大程度上依赖于原因状态c的出现,表示为


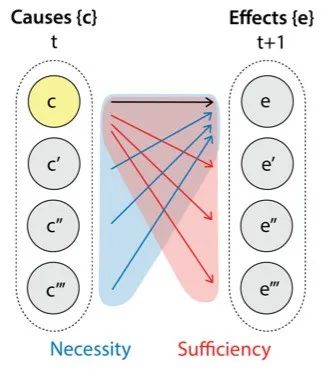
图1:确定性与必要性的图示
2.2 确定性与简并性
上述两个因果基本式sufficiency和necessity均为具体事件间的关系,我们还可以对其扩展得到另外两个基本式:确定性(determinism)和简并性(degeneracy),这种扩展使得原本的基本式更加具有泛化能力。
确定性的概念基于一个原因状态导致的结果状态分布P(e|c)的信息熵:

当原因状态c会导致单一结果状态时,该信息熵最小,值为0。当原因状态c导致的结果状态随机,即结果状态分布为所有状态概率相同的均匀分布时,信息熵最大,值为log2n,其中n为状态总数。基于此,我们定义一个原因状态的确定性为:
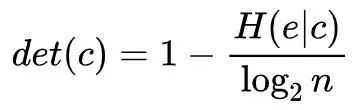
根据定义可知,确定性表示了一个原因状态导致结果状态分布的确定程度。当原因状态可以导致一个确定的结果时,其确定性为1;当原因状态对应的结果状态完全随机时,其确定性为0。我们还可以将确定性的定义扩展到系统层面:
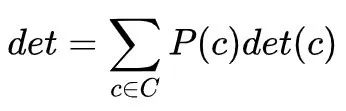

图2:因果基本式及其相互关系
类似地,我们还可以定义一个结果状态的简并性:

该基本式表示了一个结果状态对应原因状态的简并程度,来源越单一则简并性越强,反之亦然。同样的有系统层面的简并性:
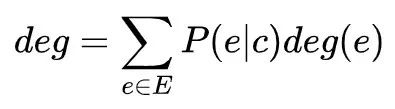
以上为全部四种基本式的定义,受篇幅限制详细推导请参考原文。
3. 基于因果基本式
对因果度量标准进行描述
基于上述因果基本式,我们可以对现有主流因果度量标准进行表述。例如Eells将原因状态与结果状态之间的因果关联强度(causal strength, CS)看作以下两个概率之差[7]:
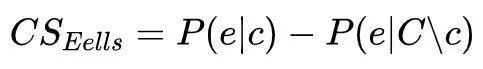
经过数学变换后我们可以发现,可以使用有效性和必要性进行表示:
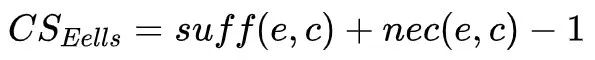
类似的我们还可以对CSLewis[8]和CSCheng[9]两种度量标准做如下变换:
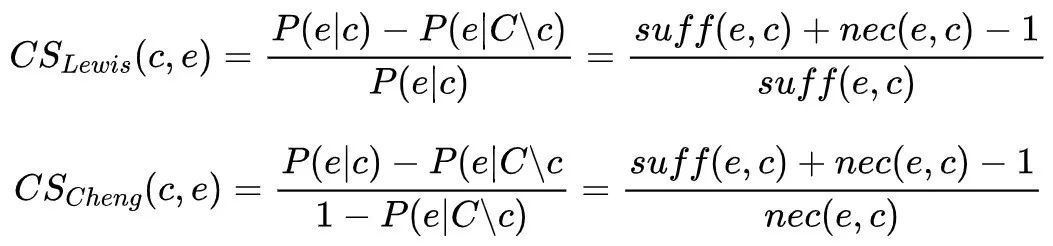
值得注意的是,上述三种度量标准均曾被因果推断领域的领军人物Judea Pearl再次独立提出过[10],受篇幅限制关于该recreation的介绍以及余下的9种度量标准的规范化请参看原文。

图3:部分因果关联强度的规范化
4. 因果涌现
在多种因果度量标准下广泛存在
为了观察上述因果度量标准的表现,作者建立了一个简单的马尔可夫链模型。微观尺度下,模型中的节点状态包含0和1两种,所有节点的状态组合则为系统的一种状态,系统状态会依照规则进行转移。图4A上为该模型的一个示例,图中的系统由三个布尔节点组成,概率转移规则由有向箭头进行描述。图4A下展现了该系统的状态转移矩阵(transition probability matrix, TPM)。基于一定的粗粒化规则,我们可以得到宏观尺度下的系统及其状态转移矩阵,如图4B所示。该图对应的粗粒化规则为ON={000, 001, 010, 011}, OFF={111, 110, 101, 100}。
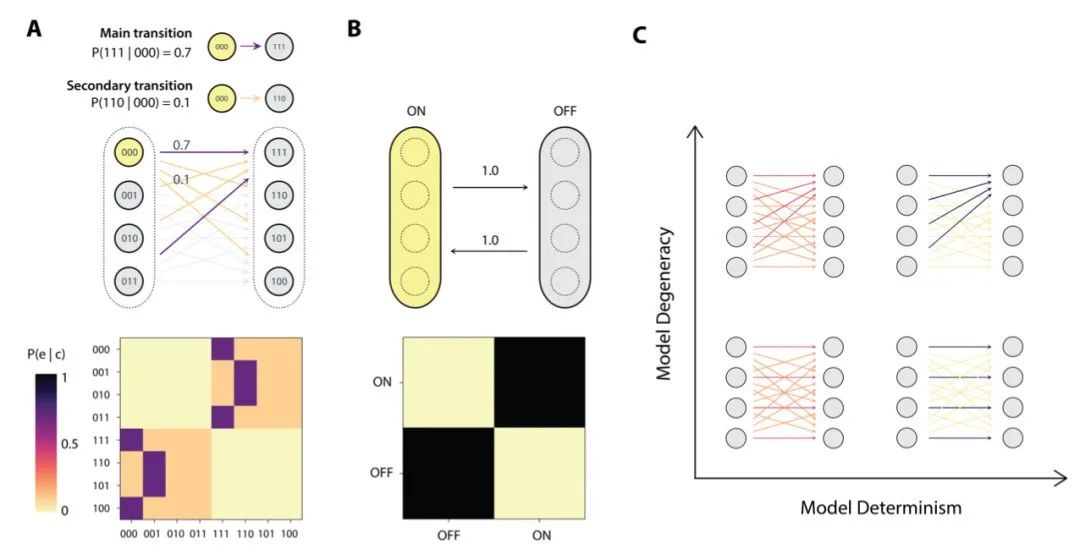
图4:A 马尔可夫链模型示意图;B 宏观尺度下的马尔可夫链模型;C 不同性质马尔可夫链模型的可视化
对比两个状态转移,我们可以定性观察到,宏观尺度下的系统间的状态有着更强的因果关系,即发生了因果涌现(Causal emergence, CE)现象。那么如何对这种现象进行定量描述呢?我们可以将因果涌现强度进行如下定量描述:
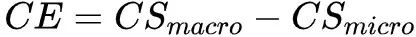
当CE为正时,则说明发生了因果涌现现象。反之则意味着因果退化(Causal reduction, CR)。
作者在与图4中相似,但节点更多、规模更大的模型上对因果涌现进行了定量计算。其中宏观与微观的因果关联强度计算方式覆盖了了上文提到所有十二种因果度量标准。在系统自身微观性质方面,作者则遍历了如图4C所示的多种不同状态转移规则。最终结果如图5所示,每个格点的颜色表示因果涌现的强度,颜色却倾向于绿色,则因果涌现强度越高。我们可以发现在不同的干预分布(关于干预分布的定义参看原文)、不同的因果度量标准下因果涌现现象都是广泛存在的。值得注意的是,由于简并性与因果关联强度负相关,故在该指标下发生的因果涌现强度为负同样意味着因果涌现。
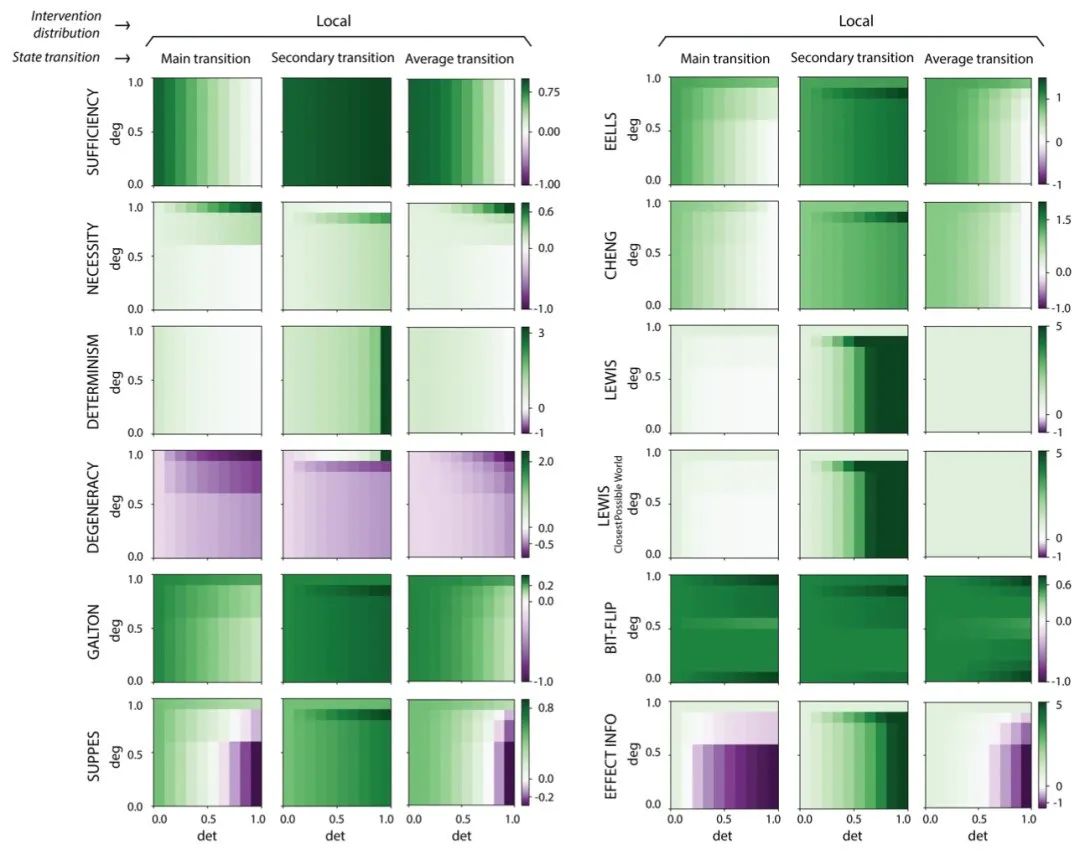
图5:因果涌现现象示意图
5. 总结
因果涌现现象是指系统在宏观下表现出更强的因果关联的现象,我们可以将其解释为宏观尺度下对系统噪声的削弱。在本篇文章中,作者使用因果基本式对主流因果关系度量指标进行了较为统一的描述,一定程度上说明了不同因果关系度量标准有着相同的数学来源,并证明了因果涌现现象在多种因果关系度量标准下广泛存在。
参考文献
1. Branden Fitelson and Christopher Hitchcock. Probabilistic Measures of Causal Strength. Causality in the Sciences, January 2010.
2. Erik P. Hoel, L. Albantakis, and G. Tononi. Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences, 110(49):19790–19795, December 2013.
3. Erik P. Hoel, Larissa Albantakis, William Marshall, and Giulio Tononi. Can the macro beat the micro? Integrated information across spatiotemporal scales. Neuroscience of Consciousness, 2016(1):niw012, 2016.
4. Joe Dewhurst. Causal emergence from effective information: Neither causal nor emergent? Thought: A Journal of Philosophy, 10(3):158–168, 2021. Publisher: John Wiley & Sons, Ltd.
5. Max Tegmark. Improved Measures of Integrated Information. PLOS Computational Biology, 12(11):e1005123, November 2016. Publisher: Public Library of Science.
6. Pedro A. M. Mediano, Fernando Rosas, Robin L. Carhart-Harris, Anil K. Seth, and Adam B. Barrett. Beyond integrated information: A taxonomy of information dynamics phenomena. arXiv:1909.02297 [physics, q-bio], September 2019. arXiv: 1909.02297.
7. Ellery Eells. Probabilistic Causality. Cambridge University Press, 1991.
8. David Lewis. Causation. Journal of Philosophy, 70(17):556–567, 1973.
9. Patricia W. Cheng and Laura R. Novick. Causes versus enabling conditions. Cognition, 40(1):83–120, August 1991.
10. Judea Pearl. Causality. Cambridge University Press, Cambridge, 2 edition, 2009.
未来智能实验室的主要工作包括:建立AI智能系统智商评测体系,开展世界人工智能智商评测;开展互联网(城市)大脑研究计划,构建互联网(城市)大脑技术和企业图谱,为提升企业,行业与城市的智能水平服务。每日推荐范围未来科技发展趋势的学习型文章。目前线上平台已收藏上千篇精华前沿科技文章和报告。
如果您对实验室的研究感兴趣,欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”

)


















)