导读:本文将介绍在广告行业中自然语言处理和推荐系统实践。本文主要分享从理论到实战知识蒸馏,对知识蒸馏感兴趣的小伙伴可以一起沟通交流。
摘要:本篇主要分享从理论到实战知识蒸馏。首先讲了下为什么要学习知识蒸馏。一切源于业务需求,BERT这种大而重的模型虽然效果好应用范围广,但是很难满足线上推理的速度要求,所以需要进行模型加速。通常主流的模型加速方法主要包括剪枝、因式分解、权值共享、量化和知识蒸馏等;然后重点讲解了知识蒸馏,主要包括知识蒸馏的作用和原理、知识蒸馏的流程以及知识蒸馏的效果等;最后理论联系实战,讲解了实际业务中主要把BERT作为老师模型去教作为学生模型的TextCNN来学习知识,从而使TextCNN不仅达到了媲美BERT的分类效果,而且还能很好的满足线上推理速度的要求。对知识蒸馏感兴趣的小伙伴可以一起沟通交流。
下面主要按照如下思维导图进行学习分享:
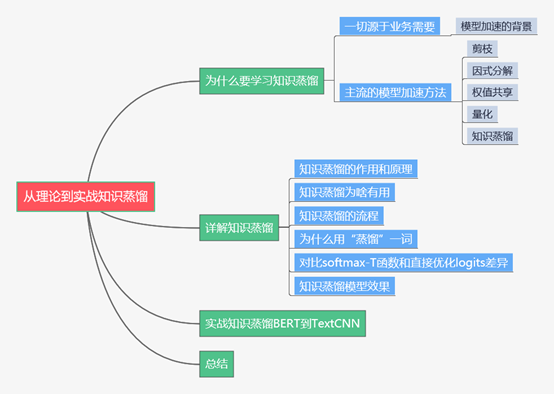
01 为什么要学习知识蒸馏
1.1 一切源于业务的需要
目前大火的BERT这一类预训练+微调的两阶段模型因为效果好和应用范围广在各种自然语言处理任务中疯狂屠榜取得state-of-art。在线下时延较低的场景下这类模型可以很好的满足业务需求,但是在线上推理场景中比如用户实时搜索返回广告就很难满足时延要求。实际业务中我们线上的文本推理时延需求是在10ms以内,因为模型太大(BERT基础版本有330M接近一亿的参数量)所以似乎很难满足线上推理的要求。
现在我们面临这样一种困境:BERT这类大模型精度高但是线上推理速度慢,传统的文本分类模型比如TextCNN等线上推理速度快(因为模型比较小)但是精度有待提升。针对上面的问题,我们的需求是获得媲美BERT等大模型的精度,还能满足线上推理速度的时延要求。
1.2 主流的模型加速方法
明确了我们的目标是获得大模型高精度的同时还能很好的满足线上推理的速度要求,这就需要用到模型加速技术。目前主流的模型加速方法主要有以下几种:
剪枝。对模型的网络进行修剪,比如减掉多余的头(因为Transformer使用多头注意力机制),或者直接粗暴的使用更少的Transformer层数;
因式分解。之前比较火的ALBERT模型使用的一个优化策略就是对embedding参数进行因式分解。因为BERT将词向量和encode输出的维度都设置为768维,而encode中包含丰富的语义信息,所以明显存储的信息量比词向量多,所以ALBERT的策略就是采用因式分解的方法把词向量映射到低维空间,这样就能大大降低参数量,最后再映射回高维的embedding向量;
权值共享。这也是ALBERT中使用的优化策略之一。对Transformer各层参数可视化分析发现各层参数类似,都是在[CLS]token和对角线上分配更多的注意力,通过多层之间共享参数从而达到了模型加速的目的。对ALBERT中因式分解和全职共享感兴趣的小伙伴可以转过头来看看我之前写的这篇文章《广告行业中那些趣事系列6:BERT线上化ALBERT优化原理及项目实践(附github)》
量化。量化操作主要是以精度换速度,业界也有尝试在BERT微调阶段进行量化感知训练,使用最小的精度损失将BERT模型参数压缩了4倍。这些量化操作方案很多也是为了将模型移植到移动端进行的优化;
知识蒸馏。知识蒸馏是把大模型或者多个模型ensemble学到的知识想办法迁移到一个轻量级的小模型上去,线上部署这个小模型就可以了。
之前在知乎上看到过有好心人整理了主流模型加速的论文分享,下面是论文分类图片,有兴趣的小伙伴可以多看看论文:
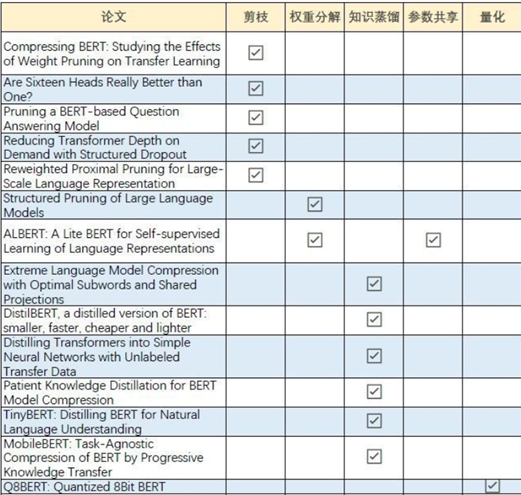
02 详解知识蒸馏
2.1 知识蒸馏的作用和原理
要搞明白知识蒸馏的作用,咱们还是拿前面的例子来说明。BERT这一类模型优点在于效果好,但是如果用于线上推理就比较麻烦了,因为基础版本的BERT模型接近330M包含一亿的参数,你想让一个一亿参数的模型完成线上10ms内的线上推理基本有点不现实。而传统的文本分类算法比如TextCNN可以轻松满足线上推理的需求,但是效果相比BERT还是有点不如人意。知识蒸馏通俗的理解就是BERT当老师,TextCNN当学生,让BERT这个老师把学到的知识传授给TextCNN这个学生,这样就能让TextCNN达到和BERT媲美的效果,最后我们线上去部署TextCNN,就能做到模型效果和线上推理速度兼得。这就是知识蒸馏的作用。
知识蒸馏的概念最早是2015年Geoffrey Hinton在《Distilling the Knowledge in a Neural Network》这篇论文中提出来的。知识蒸馏就是把一个大模型或者多个模型ensemble学到的知识迁移到另一个轻量级的单模型上,最主要的目的是为了方便线上部署。从上面的概念中也可以看出知识蒸馏主要有两个方面:第一个是将大而深的模型迁移到一个轻量级的小模型上。这就像我们线上把大而深的BERT模型学到的知识迁移到轻量级的TextCNN小模型上;另一个就是将多个模型ensemble学到的知识迁移到单个轻量级的模型。多个模型ensemble的操作在kaggle比赛中非常常见,为了提升那1到2个百分点,各种花里胡哨奇淫巧计无所不用其极。但是在工业场景中倒没有那么普遍,毕竟生产场景是要考虑投入产出比的。你得时刻掂量花了那么多时间精力以及机器算力提升的那一点点精度是不是真的划得来。而知识蒸馏就可以把多个模型ensemble学到的知识通通学到手,真正的做到集百家之长。
一点反思,感觉知识蒸馏和读书很像。一些人经历过各种酸甜苦辣学到了很多有用的知识,这些人就像老师模型一样。他们会通过写书等方式把这些知识传承下来,这时候我们可以通过读书(知识蒸馏)来学习他们的知识,就算不用去经历他们的酸甜苦辣我们照样能用学到的知识去指导我们以后的生活,相当于我们得到了“老师”的泛化能力。
2.2 知识蒸馏为啥有用
众所周知,一个好的模型最重要的是通过训练数据获得一定的泛化能力,不仅仅是拟合训练数据,最重要的是在新数据集上能有一定的泛化识别能力。而知识蒸馏的目的是让学生去学习老师的这种泛化能力,所以从理论上来说学生比老师单纯的去拟合训练数据能获得更多的知识。下面通过手写数据集的例子来说明知识蒸馏为啥能学到更多的知识:
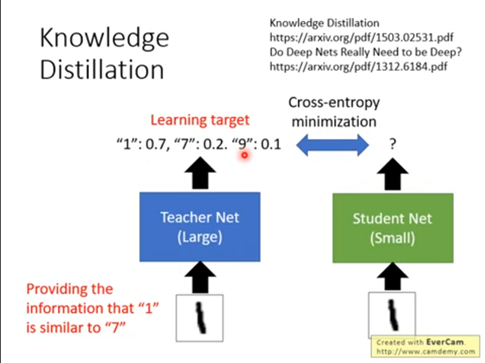
对于老师或者没有使用知识蒸馏的小模型来说,主要是通过训练数据来学习知识。我们的训练数据集是一张一张手写数字的图片,还有对应0到9十个数字的标签。在这种学习中我们可以用的只有十个类别值,比如一张手写数字1的图片样本的标签是1,告诉模型的知识就是这个样本标签是1,不是其他类别。而使用知识蒸馏的时候模型可以学到更多的知识,比如手写数字1的图片样本有0.7的可能是数字1,0.2的可能是数字7,还有0.1的可能是数字9。这非常有意思,模型不仅学到了标签本身的知识,还学习到了标签之间的关联知识,就是1和7、9可能存在某些关联,这些知识称为暗知识,这是知识蒸馏学到的知识,也是知识蒸馏有用的重要原因。
2.3 知识蒸馏的流程
知识蒸馏主要如图所示包括以下几个流程:

首先,训练一个老师模型。这里的老师模型可以是大而深的BERT类模型,也可以是多个模型ensemble集成后的模型。因为这里没有线上推理的速度要求,所以主要目标就是提升效果;
然后,设计蒸馏模型的loss函数训练学生模型,这也是最重要的步骤。蒸馏模型的loss函数定义如下:
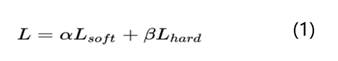
蒸馏模型的loss函数主要分成两部分:L_soft和L_hard。其中L_soft是老师教学生学习的损失函数,L_hard是学生自己跟着答案(标签)学习的损失函数,a和b(贝塔打不出来)一般相加为1。
再看看老师是怎么教学生学习的,L_soft公式具体如下图所示:
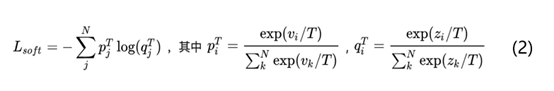
上述公式中p代表老师模型的输出结果,然后将老师模型的输出结果p作为学生模型的目标,使学生模型的输出结果q尽可能接近p,具体就是计算老师和学生的交叉熵。这里重点是T的作用,T是知识蒸馏里的超参数,论文中称为温度temperature。分类任务中一般采用的就是softmax+交叉熵的模型,当T=1时其实就是softmax函数。如果老师模型直接使用softmax函数输出结果p可能不太合适,主要原因是当一个模型训练好之后对于正确的答案一般会有很好的置信度。就像上面讲的手写数据集中图片样本1被预测为数字1的概率会很高,同时预测为其他数字的概率也会很低,比如10e-5等等。这样的情况下老师模型很难将学到的标签类型之间联系的知识传递给学生模型。
针对这个问题,知识蒸馏的作者提出了softmax-T函数,也就是通过temperature来控制老师模型输出的结果p的分布。p是学生模型学习的对象,v_i就是模型softmax前的输出logits。当T=1的时候这个公式就是softmax,根据logits输出各个类别的概率;当T接近0时,概率最大的类别输出值就会接近1,其他的输出值接近0,作用类似one-hot编码;当T越大时,会使各个类别输出的概率分布相对平缓,从而一定程度上保留了各个类别之间的联系知识;极端情况下,当T趋于无穷大时概率分布会变成一个均匀分布。温度T对softmax-T函数的概率分布影响如下图所示:

综合来说知识蒸馏通过控制超参数T使得老师模型的输出概率分布会保留类别之间的联系知识。个人觉得这也是知识蒸馏模型中最重要的知识点。
下面是L_hard损失函数公式:

L_hard其实和常规模型是一样的,就是根据训练集的label来学习。上面公式中c就是正确答案label,也就是计算学生模型的输出结果q和标签c的交叉熵。
L_soft和L_hard分别对应的是样本soft target和hard target。下面通过手写数字集样本1来对比 soft target和hard target的区别:
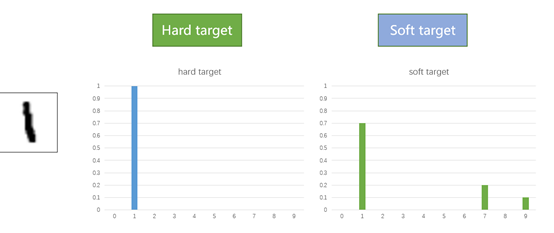
通过上图可以发现Hard target中样本的分布比较“极端”,是0或者1,而Soft target中样本的分布会更加平滑一些。
最后是使用学生模型进行线上预测。这里需要注意线上预测的时候需要把T设置回1。
2.4 为什么用“蒸馏”一词
知识蒸馏的目的是让学生模型的softmax输出结果q尽可能的接近老师模型的softmax输出结果p。一般的softmax函数中指数e会把logits之间的差距拉大,然后作归一化,使得最终得到的分布是arg max的近似,也就是其中一个类别值很大,其他类别值非常小,类似one-hot,这样使老师模型无法把标签之间的联系知识教给学生,也就是上面说的手写数字1的图片样本它有0.7的可能是数字1,0.2的可能是数字7,还有0.1的可能是数字9这样的暗知识没有办法传递给学生模型。为了让老师模型softmax输出的结果分布更平滑一些,最简单直接的做法是直接比较logits。比如z_i是学生模型产生的logits,v_i是老师模型产生的logits,其实就是最小化v_i和z_i:
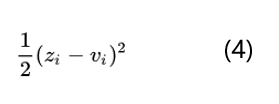
针对这个问题知识蒸馏的作者提出了softmax-T函数。这里的T是温度temperature,是统计力学中的概念。前面也说过当T趋于0时softmax的输出结果会接近one-hot编码,也就是一个类别值接近1,其他类别接近0;当T趋向于无穷的时候,softmax的输出会趋向于均匀分布。
利用这个特性我们会在训练学生分类器的时候设置较高的T使得softmax输出的结果具有一定的平滑性,作用自然是学习类别之间的联系知识,也让学生模型的输出尽可能接近老师模型。当学生模型训练完成之后再把T设置为1来进行线上预测。
之所以叫“蒸馏”也是和化学中的蒸馏概念接近。化学中通过蒸馏的方法可以把不同沸点的物质区分开,流程就是升温把低沸点的物质汽化,然后迅速降温冷凝从而达到分离物质的目的。对比下知识蒸馏的概念也是这样,学生模型训练时增加温度参数T,然后在线上预测的时候降低温度T为1从而将老师模型中的知识提取出来,这和化学中的蒸馏流程非常类似。这可能也是作者命名为知识蒸馏的一个原因吧。
2.5 对比softmax-T函数和直接优化logits差异
上面也说过知识蒸馏中最有价值的就是通过softmax-T使得老师模型的softmax输出结果包含类别之间联系的暗知识,所以这里咱们再深入了解下softmax-T和直接优化logits也就是公式4之间的差异。学生模型训练时我们需要最小化老师分布和学生分布的交叉熵,下面是最小化交叉熵的公式:
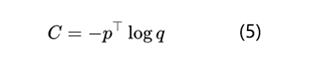
根据公式2和公式5,计算学生模型交叉熵对某个logits分布z_i的梯度就是:
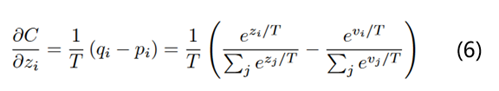
回顾点高数知识,当x趋于0的时候,exp(x)-1和x是等价无穷小的。也就是说当T无穷大的时候,就变成了如下的公式:
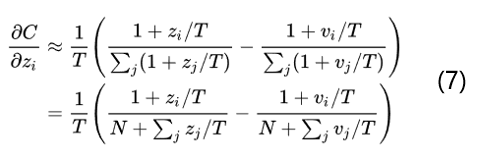
当所有的logits对每个样本都是零均值化时, z_j的求和=v_j的求和=0,那么就变成了如下的公式:
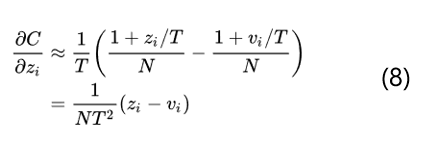
得到了公式8就可以看出当T足够大并且logits对所有样本都是零均值化的时候知识蒸馏和最小化logits的平方差也就是公式4是等价的。所以总体来说通过softmax-T不仅和最小化logits是等价的,而且还可以通过控制超参数T来调节老师模型的输出结果分布,具有很好的灵活性。
2.6 知识蒸馏模型效果
知识蒸馏模型的作者主要进行了以下三个实验:
第一个实验是验证可以将大而深的模型知识转移到小模型上。在MNIST数据集上先使用大而深的模型进行训练,测试集中有67个错误;然后使用小模型进行训练,测试集中有146个错误;最后使用知识蒸馏的方法在目标函数中加入L_soft,学生模型在测试集中错误变成了74个。通过这个实验可以看出知识蒸馏的确可以使学生模型获得老师模型的知识从而提升小模型的效果。有趣的是作者还发现即使在训练集中不包含某一类的训练数据,通过知识蒸馏的方法在测试集中竟然能识别到没有包含这一类标签的数据。也就是说在训练集中可能学生模型从来没见过3,但是在测试集中竟然有识别3的能力。厉害不?
第二个实验主要是验证将多个模型ensemble得到的知识转移到单一模型上。在语音识别任务中首先训练了10个DNN模型,然后通过ensemble的方式得到最终的模型,经过ensemble得到的模型效果是优于任意单个模型的;然后将这10个DNN模型作为老师模型去训练学生模型,得到的学生模型效果是优于任意一个老师模型的,可以看出经过知识蒸馏得到的学生模型的确学习到了老师模型的知识。下面是详细实验结果:
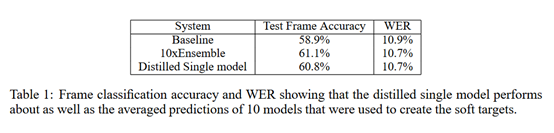
03 实战知识蒸馏BERT到TextCNN
实际业务中我们线下场景因为没有时延的要求所以主要使用BERT模型来完成文本分类任务。而对于线上推理任务分别尝试了FastBERT、ALBERT等等貌似都达不到10ms的时延要求,目前主要使用知识蒸馏的方法来进行模型加速。将BERT作为老师模型,把 TextCNN作为学生模型来学习老师的知识。按照目前的实验效果来看,TextCNN学到了BERT的知识,在测试集和真实分布数据集上的效果良好,推理速度也是满足时延的。
构造TextCNN代码如下:
class TextCNN(object): """ 利用bert作为teacher,指导textcnn学习logits,损失函数为KL散度 """ def __init__( self, sequence_length, vocab_size, embedding_size, filter_sizes, num_filters,dropout_keep_prob=0.2): self.dropout_keep_prob = dropout_keep_prob # Placeholders for input, output self.input_x = tf.placeholder(tf.int32, [None, sequence_length], name="input_x") self.labels = tf.placeholder(tf.int32, shape=None, name="labels") self.teacher_logits = tf.placeholder(tf.float32, shape=None, name="teacher_logits") # Embedding layer # with tf.device('/cpu:0'), tf.name_scope("embedding"): with tf.name_scope("embedding"): self.W = tf.Variable( tf.random_uniform([vocab_size, embedding_size], -1.0, 1.0), name="W") self.embedded_chars = tf.nn.embedding_lookup(self.W, self.input_x) self.embedded_chars_expanded = tf.expand_dims(self.embedded_chars, -1) # Create a convolution + maxpool layer for each filter size # textcnn模型结构 pooled_outputs = [] for i, filter_size in enumerate(filter_sizes): with tf.name_scope("conv-maxpool-%s" % filter_size): # Convolution Layer filter_shape = [filter_size, embedding_size, 1, num_filters] W = tf.Variable(tf.truncated_normal(filter_shape, stddev=0.1), name="W") b = tf.Variable(tf.constant(0.1, shape=[num_filters]), name="b") conv = tf.nn.conv2d( self.embedded_chars_expanded, W, strides=[1, 1, 1, 1], padding="VALID", name="conv") h = tf.nn.relu(tf.nn.bias_add(conv, b), name="relu") # Maxpooling over the outputs pooled = tf.nn.max_pool( h, ksize=[1, sequence_length - filter_size + 1, 1, 1], strides=[1, 1, 1, 1], padding='VALID', name="pool") pooled_outputs.append(pooled) # Combine all the pooled features num_filters_total = num_filters * len(filter_sizes) self.h_pool = tf.concat(pooled_outputs, 3) self.h_pool_flat = tf.reshape(self.h_pool, [-1, num_filters_total]) # Add dropout with tf.name_scope("dropout"): self.h_drop = tf.nn.dropout(self.h_pool_flat, self.dropout_keep_prob) l2_loss = tf.constant(0.0) num_classes = 2 # Final (unnormalized) scores and predictions with tf.name_scope("output"): W = tf.get_variable( "W", shape=[num_filters_total, num_classes], initializer=tf.contrib.layers.xavier_initializer()) b = tf.Variable(tf.constant(0.1, shape=[num_classes]), name="b") l2_loss += tf.nn.l2_loss(W) l2_loss += tf.nn.l2_loss(b) self.scores = tf.nn.xw_plus_b(self.h_drop, W, b, name="scores")[:,1] self.logits = tf.nn.softmax(self.scores) tf.add_to_collection("logits", self.logits) with tf.name_scope("loss"): loss = 0.1*tf.nn.softmax_cross_entropy_with_logits(logits=self.logits, labels=self.labels) loss = tf.reduce_sum(loss) self.loss = loss + 0.9*tf.keras.losses.KLDivergence()(tf.nn.log_softmax(self.scores), self.teacher_logits) 





)












