目录
0.上节回顾
1. Perceptron Hypothesis Set
2. Perceptron Learning Algorithm(PLA)(重点)
3. Guarantee of PLA(难点)
4. Non-Separable Data
0.上节回顾
第一节课主要讲述了机器学习的定义及机器学习的过程,主要如下图。我们有数据集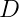


第2节课主要介绍了感知机和我们学到的第一个算法:Perceptron Learning Algorithm(PLA)。
1. Perceptron Hypothesis Set
还是来看一个简单的例子:我们根据消费者的特征来决定是否批发信用卡;如下图所示。消费者的特征有:年龄、年薪、工作时间、欠款等。我们有一个线性模型,根据计算出的结果来决定是否批发信用卡,我们的目标就是求出权重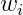

下面是感知机的向量形式,我们也可以把阈值当作权重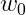
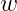
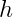

我们可以在二维平面内画出我们的感知机,由下图可知,消费者特征是图上的点(特征数量为2),标签有两种结果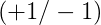

2. Perceptron Learning Algorithm(PLA)
根据上一部分的介绍,我们已经知道了hypothesis set由许多条直线构成。我们的目的就是如何设计一个演算法A,来选择一个最好的直线,能将平面上所有的正类和负类完全分开,也就是找到最好的g,使g≈f(目标函数)。
我们可以使用逐点修正的思想,首先在平面上随意取一条直线,看看哪些点分类错误。然后开始对第一个错误点就行修正,即变换直线的位置,使这个错误点变成分类正确的点。接着,再对第二个、第三个等所有的错误分类点就行直线纠正,直到所有的点都完全分类正确了,就得到了最好的直线。这种“逐步修正”,就是PLA思想所在。


下面是一个PLA的修正实例:











对PLA,我们需要考虑以下两个问题:
-
PLA迭代一定会停下来吗?如果线性不可分怎么办?
-
PLA停下来的时候,是否能保证f≈g?如果没有停下来,是否有f≈g?
3. Guarantee of PLA
根据PLA的定义,当找到一条直线,能将所有平面上的点都分类正确,那么PLA就停止了。要达到这个终止条件,就必须保证D是线性可分(linear separable)。如果是非线性可分的,那么,PLA就不会停止。如下图所示:

对于线性可分的情况,如果有这样一条直线,能够将正类和负类完全分开,令这时候的目标权重为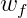

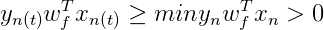
且随着PLA每次的修正,权重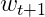
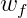


下面给出了迭代次数T的取值范围,感兴趣的可以推一下。证明链接为:http://www.cnblogs.com/HappyAngel/p/3456762.html

4. Non-Separable Data
上一部分,我们证明了线性可分的情况下,PLA是可以停下来并正确分类的,但对于非线性可分的情况,
在非线性情况下,我们可以把条件放松,即不苛求每个点都分类正确,而是容忍有错误点,取错误点的个数最少时的权重w:

下面是我们修改后的算法(Pocket算法),可以求出最值。

简单总结一下本节课介绍的内容:感知机预测集合、PLA算法、非线性可分数据的求最值方法。


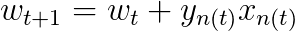
)




)
下gcc-linaro-arm-linux-gnueabihf交叉编译环境安装)
tomcat与九大内置对象)

)
)


机器学习基石笔记 Lecture3:Types of Learning)
)

 JSP详解(四大作用域九大内置对象等))

)
