exus3.x.x上传第三方jar:
1. create repository
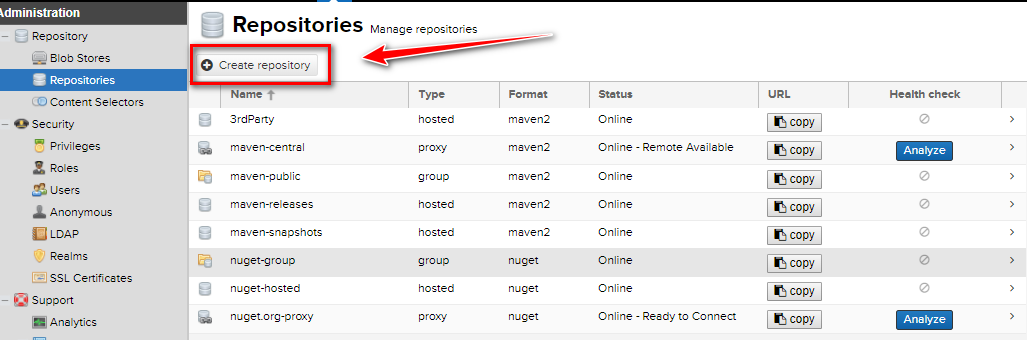
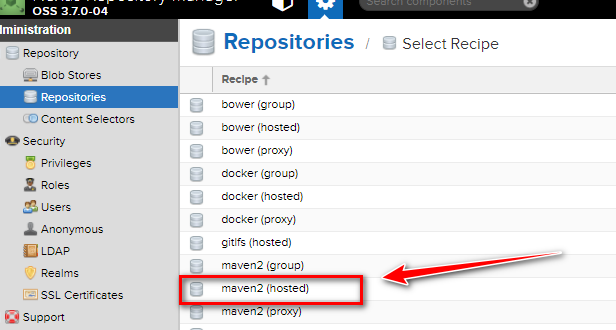
选择maven2(hosted),说明:
proxy:即你可以设置代理,设置了代理之后,在你的nexus中找不到的依赖就会去配置的代理的地址中找hosted:你可以上传你自己的项目到这里面group:它可以包含前面两个,是一个聚合体。一般用来给客户一个访问nexus的统一地址。简单的说,就是你可以上传私有的项目到hosted,以及配置proxy以获取第三方的依赖(比如可以配置中央仓库的地址)。前面两个都 弄好了之后,在通过group聚合给客户提供统一的访问地址。
新建的 reposity 参数如下:

2.赋权
修改maven安装目录下的 /conf/settings.xml 文件,添加server 节点。如图:

3.上传 jar 包
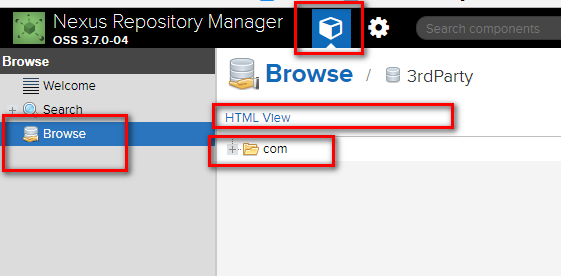
mvn deploy:deploy-file -DgroupId=xxx.xxx -DartifactId=xxx -Dversion=0.0.2 -Dpackaging=jar -Dfile=D:\xxx.jar -Durl=http://xxx.xxx.xxx.xxx:8081/repository/3rdParty/ -DrepositoryId=3rdParty 其中-DgroupId 为上传的jar的groupId-DartifactId 为上传的jar的artifactId-Dversion 为上传的jar的需要被依赖的时候的版本号然后是-Dpackaging为jar,-Dfile为jar包路径 -Durl 为要上传的路径,可以通过以下方式获取到
举个例子:
mvn deploy:deploy-file -DgroupId=com.google.guava -DartifactId=guava -Dversion=22.0 -Dpackaging=jar -Dfile=D:\temp\guava-22.0.jar -Durl=http://192.168.178.132:8081/repository/3rdParty/ -DrepositoryId=3rdParty
完成 !!!


)







)








