粒子群算法组卷_粒子群（PSO）算法概念及代码实现

粒子群算法的由来及思想

粒子群算法最早是由两名美国的科学家基于群鸟觅食，寻找最佳觅食区域的过程所提出来的，作为一种智能算法，PSO模拟的就是最佳决策的过程，鸟群觅食类似于人类的决策过程，想想在你做出选择之前，是不是会受到自己的经验（局部最优）以及周围人的经历（全局最优）的影响？同样的道理，群鸟在觅食的过程当中，每一只鸟的初始位置都处于随机状态，当然也不知道最佳的觅食点在何处，并且每只鸟的飞行方向也是随机的。可以认为，在觅食的初期，鸟群的运动轨迹都是杂乱无章的，随着时间的推移，处于随机位置的鸟类通过群内的相互学习、共享觅食信息，每一只鸟在每一次的觅食过程中结合自己的经验和同伴传送的信息估计目前所处的位置能够找到食物有多大的价值。基于这样的搜索方式，粒子群算法（Particle Swarm Optimization,PSO）应运而生。

基本概念

每只鸟在某处位置能够找到食物的可能可以通过适应值来刻画，每只鸟能够记住自己的觅食位置，并且找到其中的最佳位置（局部最优），鸟群中所有个体的最佳位置就可以看做整个鸟群的最佳觅食点（全局最优）。可以预见的是，整个鸟群的觅食活动总体上一定是往这个全局最优的觅食区域运动的，通过鸟群觅食位置的不断移动即不断地迭代，速度的不断更新，鸟群往该最优位置步步逼近。

鸟群中的每一个个体都可以当做一个粒子，鸟群即可被看做粒子群。假设一个有M个粒子的粒子群在一个N维空间内寻找最优位置，那么可以对每个粒子赋予一个“位置”：

对于每一个粒子而言，该位置即为问题的一个潜在解，在这个位置能觅到食物的可能性有多大呢？既可以通过将
带入目标函数计算其适应值，根据适应值大小来衡量其优劣。在每一次的搜寻过程中，记录每个粒子的最优位置：

在本次觅食搜寻过程中，所有粒子最优位置的最优解即可当做整个粒子群的最佳觅食位置：

反复进行食物的搜寻过程（进行迭代），直至找到全局最优解为止。当然在每一次位置的寻找之后，应该对粒子的速度和所在位置进行更新，记第i个粒子的速度为：

粒子的速度及位置更新的方式如下：

其中
是一个非负数，称为惯性因子，对算法的收敛起到很大的作用，其值越大，粒子飞跃的范围就越广，更容易找到全局最优，但是也会错失局部搜寻的能力。
分别为局部和全局最优位置。
加速常数
也是非负常数，是调整局部最优值和全局最优值权重的参数，如果前者为0说明搜寻过程中没有自身经验只有社会经验，容易陷入局部最优解；若后者为0，即只有社会经验，没有自身经验，常常会陷入局部最优解中，不能飞越该局部最优区域。
是[0,1]范围之内的随机数，
是约束因子，目的是控制速度的权重。

从上面速度和位置分量的改变规则我们可以看到，速度的存在的根本作用还是为了改变粒子的位置，计算新一轮粒子的适应值，其中的参数的设置也会影响到对全局最优解的搜寻。在一般情况下，我们会对粒子的速度分量进行限制，

,如果粒子的速度分量在更新之后超过最大飞翔速度，则应该根据不同的情况进行优化问题的设定。

迭代终止条件根据具体问题而定，一般达到预定最大迭代次数或者粒子群目前为止搜寻到的最优位置满足目标函数的最小容许误差。

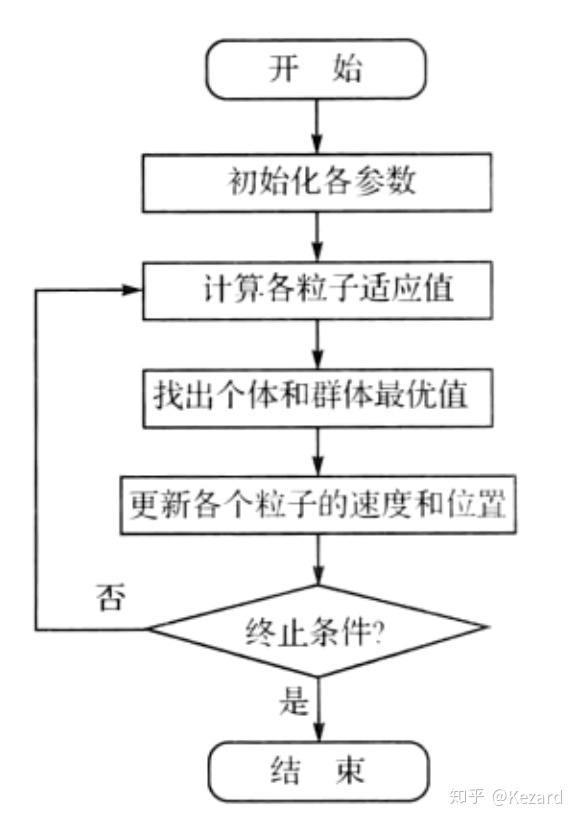
PSO算法的主要实现步骤

初始化粒子群。包括粒子的初始位置及速度，惯性因子等参数值

粒子数M一般选取20~40个，不过对于一些特殊的难题需要更多的粒子，粒子数量越多，搜索范围就越广，越容易找到全局最优解，但是也会带来更大的计算消耗。

2. 评价各个粒子的初始适应值。

3. 将初始的适应值作为各个粒子的局部最优解，保存各粒子的最优位置。并找到其中的最优值，作为全局最优解的初值，并记录其位置

4. 更新粒子速度及位置

5. 计算更新后粒子的适应值，更新每个粒子的局部最优值以及整个粒子群的全局最优值。

6. 重复4~5直至满足迭代结束条件

图1 程序设计流程图

粒子群算法的matlab程序实现

问题1：求解
之间的最小值

% 目标函数
function f=target(x)
%x in[0,9]
f=x+6*sin(4.*x)+9*cos(5.*x);
end

主程序：PSO.m

%looking for min-functinal value using "Practicle Swarm Optimization"function [Gbest_x,Gbest_y]=PSO()
%Parameter settings
lower_bound = 0;
higher_bound = 9;
particle = 20;                            % 粒子个数
max_iteration = 100;                      % 最大迭代数
dimension = 1;                            % 粒子位置的维度，即自变量个数
c1 = 2;                                   % 加速常数1，控制局部最优解
c2 = 2;                                   % 加速常数2，控制全局最优解
w = 0.6;                                  % 惯性因子
vmax = 0.8;                               % 速度最大值
precision=0.001;                          % 精度设置%Initialize
x = lower_bound+rand(particle,dimension).*(higher_bound-lower_bound);
v = 2*rand(particle,dimension);
Pbest_x=x;                                % 将初始位置设置为局部最优解的位置
Pbest_y=target(x);                        % 各个粒子的函数值作为其局部最优解
Gbest_y=inf;                              % 全局最优解的初始值设置为inf
Gbest_x = x(1,:);                         % 初始全局最优位置设定为第一个粒子的位置
k=1;
f=zeros(particle,1);%plot the function
horizon = linspace(0,9,500);
vertical = target(horizon);
plot(horizon,vertical);
hold on
[m,index] = min(vertical);
text(horizon(index)+0.5,m,['{F_{min}}= ',num2str(m)])
pic_num = 1;while k<=max_iterationflagx=Gbest_x;flagy=Gbest_y;% 搜寻各个粒子的局部最优for i=1:particlef(i) = target(x(i,:));if f(i)<Pbest_y(i)Pbest_y(i)=f(i);      % Personal best function valuePbest_x(i)=x(i,:);    % Personal best variableendend% 更新全局最优位置及适应值[Gbest_y,index] = min(Pbest_y);Gbest_x = x(index,:);% 每一次搜寻之后更新粒子的速度及位置for n=1:particlev(n,:)=w*v(n,:)+c1*rand()*(Pbest_x(n,:)-x(n,:))+c2*rand()*(Gbest_x-x(n,:));% 速度越界操作for p=1:dimensionif v(n,p)>vmaxv(n,p)=vmax;elseif v(n,p)<-vmaxv(n,p)=-vmax;endendx(n,:)=x(n,:)+v(n,:);end% 获取动态搜寻过程gif图figure(1)scatter(Gbest_x,target(Gbest_x))hold onh1=text(6,-4,['X by TSO=',num2str(Gbest_x)]);h2=text(6,-6,['Y by TSO=',num2str(target(Gbest_x))]);pause(0.2)drawnow;F=getframe(gcf);I=frame2im(F);[I,map]=rgb2ind(I,256);if pic_num == 1imwrite(I,map,'PSO.gif','gif', 'Loopcount',inf,'DelayTime',0.2);elseimwrite(I,map,'PSO.gif','gif','WriteMode','append','DelayTime',0.2);enddelete(h1);delete(h2)pic_num = pic_num + 1;% 如果迭代前后全局最优解的差小于精度要求退出if abs(flagx-Gbest_x)<precision&&abs(flagy-Gbest_y)<precisionbreakelsek=k+1;endendstring=['Min-value by TSO is ',num2str(Gbest_y),', where x= ',num2str(Gbest_x)];
title(string)

其中一次运行结果：

>> [Gbest_x,Gbest_y]=PSO();
>> Gbest_x
Gbest_x =4.3744
>> Gbest_y
Gbest_y =-10.4199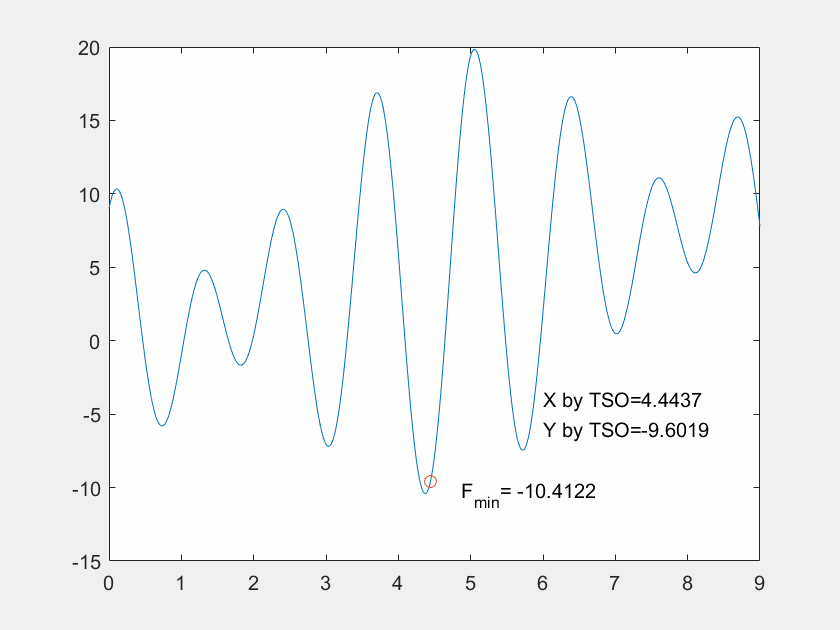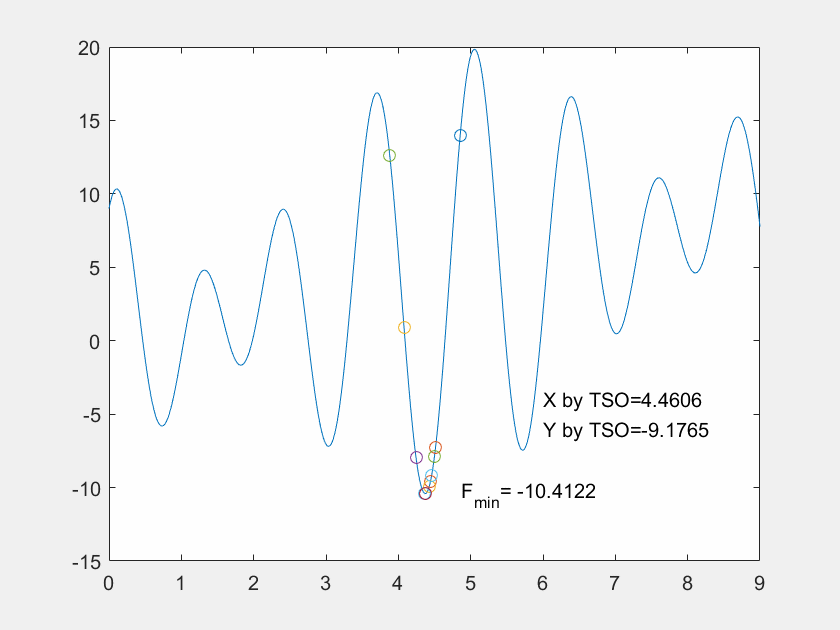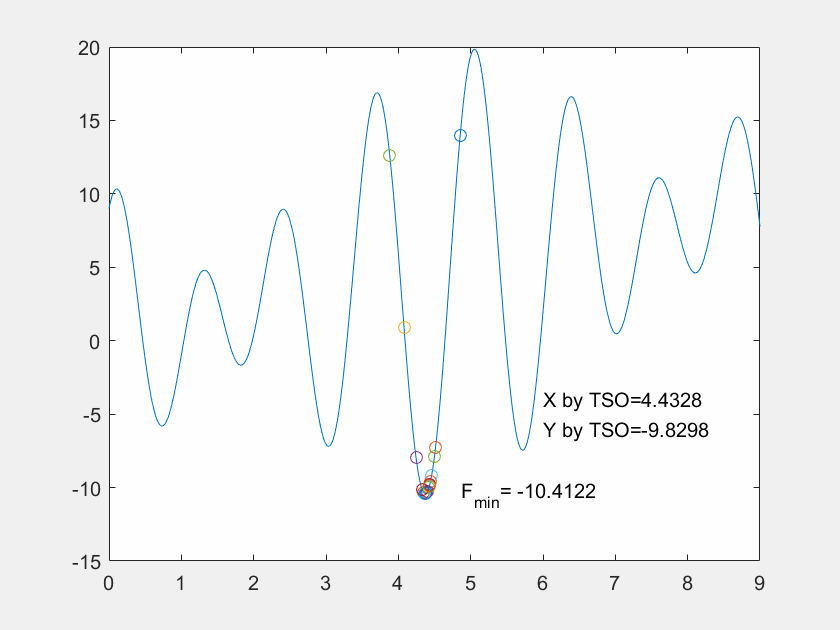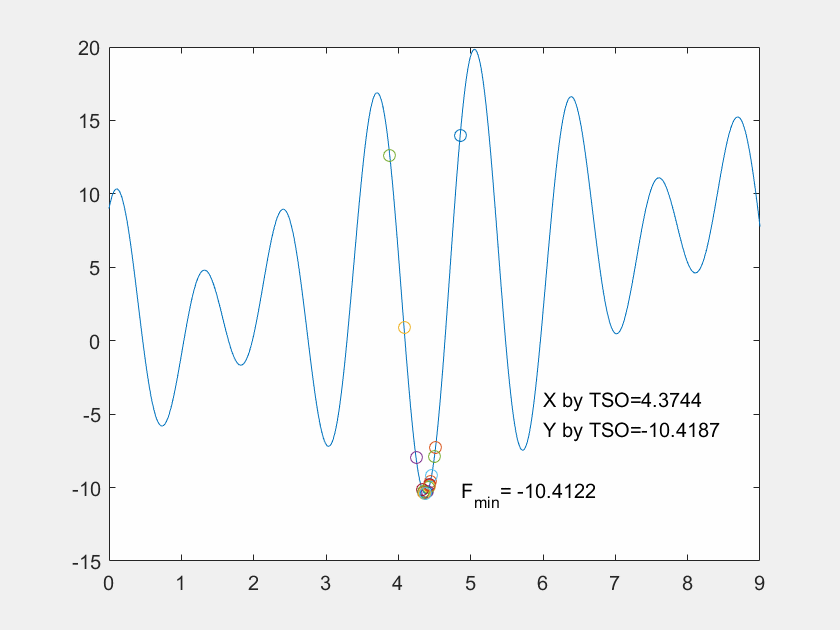

图2 PSO算法求一元函数最小值

可见，最终在x=4.3744处找到的全局最优解-10.4199，与函数的最小值

=- 10.4122相差不大。手链效果也较好。

问题2：PSO算法求解背包问题

背包问题：现有一小偷入室盗窃，可以偷窃的物品数量共有12件，物品对应的价值（万）为[5;10;13;4;3;11;13;10;8;16;7;4]；重量（千克）为[2;5;18;3;2;5;10;4;11;7;14;6]。若小偷能拿的物品总质量最大为46kg，如何选取物品使得总价值最大？

%目标函数
function f = target_BAG(x,value,weight,ratio,restriction)
Money = sum(x*value);
Lost = sum(x*weight);
if Lost < restrictionf = Money;
elsex=~x;Money = sum(x*value);f = Money-round((Lost-restriction)*ratio);
end

目标函数用于计算小偷所投物品的质量及价值，如果此时的重量超过了限制，就将所偷物品价值减小。

function [GBest_x,GBest_y,Record]= PSO_BAG()
value = [5;10;13;4;3;11;13;10;8;16;7;4];    % 物品重量
weight = [2;5;18;3;2;5;10;4;11;7;14;6];     % 物品价值
restriction = 46;                           % 背包重量限制
practicle = 20;                             % 粒子数
max_iteration = 100;
dimension = size(value,1);                  
ratio = 2.5; 
c1 = 2;                                   
c2 = 2;                                   
wmin = 0.6;
wmax = 0.8;
vmax = 0.8;                               
time=1;
%Initialize
x = round(rand(practicle,dimension));             % 背包问题中的粒子取值为0或1，代表选择物品或不选择物品
v=rand(practicle,dimension)*(2*vmax)-vmax;PBest_x = x;
PBest_y = zeros(1,dimension);
for i=1:practiclePBest_y(i) = target_BAG(PBest_x(i,:),value,weight,ratio,restriction);    %将总价值作为局部最优解
endGBest_x = ones(1,dimension);
GBest_y = 0;
Record = zeros(1,max_iteration);
for j=1:practicleif PBest_y(j)>GBest_yGBest_y = PBest_y(j);GBest_x = x(j,:);end
endwhile time<=max_iteration% Personal-Best searchingfor i=1:practiclef = target_BAG(x(i,:),value,weight,ratio,restriction);if f>PBest_y(i)PBest_y(i)=f;PBest_x(i,:)=x(i,:);end% Global Best searchingif PBest_y(i) > GBest_yGBest_y = PBest_y(i);GBest_x = PBest_x(i,:);end% Updating the speed and positionw=wmin+rand()*(wmax-wmin);      % weight is dynamicv(i,:) = w*v(i,:) + c1*rand()*(PBest_x(i,:)-x(i,:)) + c2*rand()*(GBest_x-x(i,:));for ii=1:dimensionif (v(i,ii)<-vmax)||(v(i,ii)>vmax)v(i,ii)=rand*(2*vmax)-vmax;endendvv(i,:)=1./(1+exp(-v(i,:)));for k=1:dimensionif vv(i,k)>randx(i,k)=1;elsex(i,k)=0;endendendRecord(k) = GBest_y;time = time+1;
endM = GBest_y;           % the value of the bag
N = GBest_x*weight;    % the weight of the bag
disp('---------------------------------------')
disp(['The final steal value is:',num2str(M)]);
disp(['The final steal weight is:',num2str(N)]);
string=strcat('Steal items:',num2str(GBest_x));
disp(string)

其中一次运行结果：

---------------------------------------
The final steal value is:76
The final steal weight is:44
Steal items:1  1  0  1  1  1  1  1  0  1  0  1选取第1,2,4,5,6,7,8,10,12个物品，总价值为76，总重量为44.

当然，PSO是一个基于概率的随机自搜索算法，每次的搜索结果都不尽相同，但是若算法的收敛性表现的较好，也可以认为对算法的设计是合理的。