💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码及文章
💥1 概述
文献来源:

摘要:
我们提出了一种在泊松噪声存在下图像恢复的快速算法。我们的方法基于(1)最小化泊松噪声MSE的无偏估计,(2)去噪过程的线性参数化,以及(3)在Haar DWT内跨尺度保存泊松统计。MSE估计的最小化在每个小波子带中独立执行,但由于Haar小波的正交性,这相当于全局图像域MSE最小化。这是与标准泊松噪声消除方法的重要区别,特别是那些依赖于数据的非线性预处理来稳定方差的方法。我们的非冗余尺度间小波阈值优于标准方差稳定方案,即使后者应用于平移不变设置(周期旋转)。它还实现了类似于专门为泊松数据开发的最先进的多尺度方法的质量。考虑到我们方法的计算复杂度要低几个数量级,它是一种非常有竞争力的替代方案。所提出的方法在低信号强度和/或大型数据集的背景下特别有前途。这通过生物样品的低计数荧光显微照片的去噪实验来说明。
关键词:
鱼 鳞间 降噪 小波 风险评估 阈值的线性扩展 荧光显微镜
原文摘要:
We present a fast algorithm for image restoration in the presence of Poisson noise. Our approach is based on (1) the minimization of an unbiased estimate of the MSE for Poisson noise, (2) a linear parametrization of the denoising process and (3) the preservation of Poisson statistics across scales within the Haar DWT. The minimization of the MSE estimate is performed independently in each wavelet subband, but this is equivalent to a global image-domain MSE minimization, thanks to the orthogonality of Haar wavelets. This is an important difference with standard Poisson noise-removal methods, in particular those that rely on a non-linear preprocessing of the data to stabilize the variance.Our non-redundant interscale wavelet thresholding outperforms standard variance-stabilizing schemes, even when the latter are applied in a translation-invariant setting (cycle-spinning). It also achieves a quality similar to a state-of-the-art multiscale method that was specially developed for Poisson data. Considering that the computational complexity of our method is orders of magnitude lower, it is a very competitive alternative.The proposed approach is particularly promising in the context of low signal intensities and/or large data sets. This is illustrated experimentally with the denoising of low-count fluorescence micrographs of a biological sample.
关键词:
poisson interscale denoising wavelets risk estimation linear expansion of thresholds fluorescence microscopy
📚2 运行结果

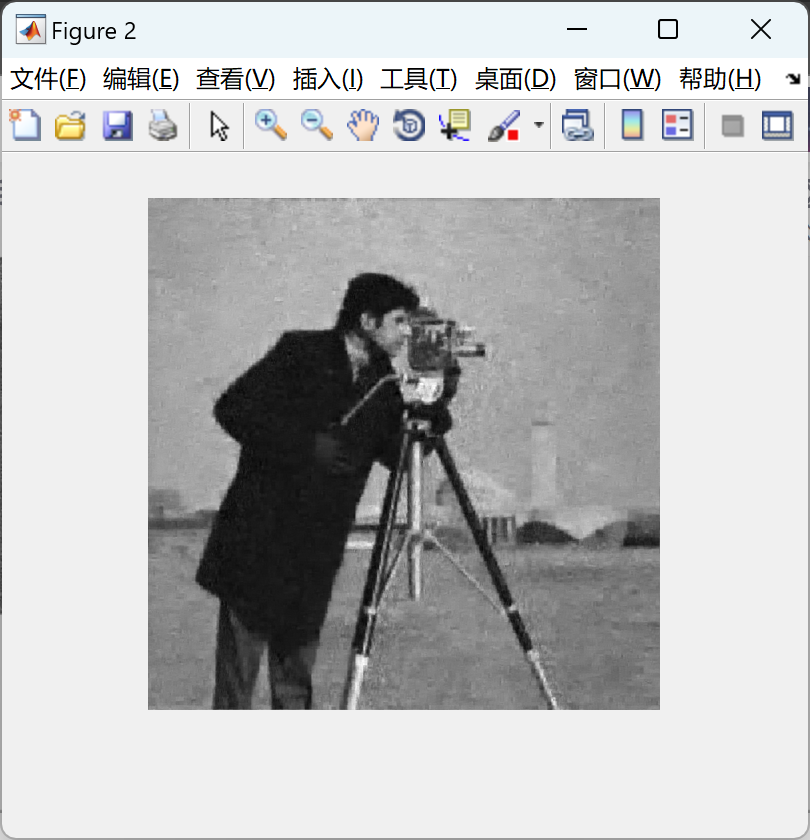
部分代码:
% Y = FAST_CCONV2(X,H,OPT)
% Performs 2D circular convolution. This implementation is fast since it
% uses FFT2 and IFFT2.
%
% Input Parameters:
% X = Input Image.
% H = 2D filter.
% OPT = 'null': No effect, (default option)
% 'nc_shift': treats H as a noncausal filter with origin at
% floor(size(H)/2); the output is shifted by the above
% amount in up-and-left direction to correct the origin.
%
% Output Parameters:
% Y = Circular convolution of X and H. No. of rows of Y is the maximum of
% the number of rows of X and that of H. Simlilarly the no. of columns
% of Y.
function y = fast_cconv2(x,h,opt)
if(~exist('opt','var'))
opt = 'null';
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] F. Luisier, C. Vonesch, T. Blu, M. Unser, "Fast Interscale Wavelet Denoising of Poisson-corrupted Images", Signal Processing, vol. 90, no. 2, pp. 415-427, February 2010.



![[JAVAee]多线程环境下:HashTable, HashMap, ConcurrentHashMap之间的区别](http://pic.xiahunao.cn/[JAVAee]多线程环境下:HashTable, HashMap, ConcurrentHashMap之间的区别)

的使用)




)

![[git] git基础知识](http://pic.xiahunao.cn/[git] git基础知识)



如何生成并添加公钥配置用户信息)


)
