文、理科数学大部分知识点、甚至相关知识点的考查形式都是共同的,甚至往年理科题目过几年就会出现在文科试卷上,反之亦然;「射影定理」是「余弦定理」的直接来源,所以不算超纲知识点。

先发福利:这里有6场「高考数学」系列Live的讲义,全拿去,送给你——《高考数学:免费送你六场Live的全部资料》【点击领取】
* 手把手为你精析100道高考真题,欢迎关注:
高考数学 | 高频真题100讲zhuanlan.zhihu.com
我们在之前的第5讲【点击回顾】里基于2013年高考数学全国II卷理科数学的第17题来为你解释在「解三角形」这一板块内使用「正弦定理」进行「边角互化」的基本原则,我把这道题目的题目重新展示给你:

上一讲中我们从稳扎稳打的常规解法中解释了每一步公式代换的思路来源,但是这道题目其实还包含了更深刻的洞见、今天我想向你拆解这道题目背后蕴含的另一个知识点——从中你也许可以体察到高考命题人的构题思路以备考原则。
我以前针对高中数学的备考原则和思路,讲过一次2个多小时的课程【点击学习】,里面就提到过这道题,但我今天的重点是:这道题目背后有更简便的想法——请注意:简便的算法还不是我的重点,我要强调的是这个简便算法背后蕴含的一条洞见。
这个比较简便的算法长成下面这样:

你看,答案只有3行,还有1行是抄题目,和之前4个步骤堆积的答案相比,这种解法就应该算是「非常好用」了吧?
它为什么好用?因为这种解法观察到了条件
与下面这个公式在形式上的相似之处:
——而(*)式有一个自己的名字,它叫「射影定理」。
「射影定理」并不是《高考大纲》明确写出的知识点,但在2013年的主观题判卷过程中,使用这个方法答题的学生步骤均可以被判满分——换言之,在高考数学阅卷组的评分细则里:「射影定理」不算超纲知识点。
P.S. 根据高考阅卷保密协议,评分细则只有5年的有效期,所以2013年的这道题目的评分细则正好今年可以讲了~
事实上这种形式的题目绝对不是个例,2017年——这是一个多么晚近的时间——同样的公式再次出现在了全国课标卷的试卷上,而且这次、它是作为文科的压轴填空题出现的:

请你注意它的题目条件,熟悉吗?
如果你考虑到下面这条射影定理:
那么这个题目右侧其实就是个
所以在这里说句题外话:有很多学生问我文科考生是不是不需要做理科题目,或者说理科生是不是不应该做文科题?我这两道「2017年全国II卷文科数学 & 2013年全国II卷理科数学」的题目的对比已经回答了你们的疑惑,在未来我们专栏【点击关注】的讲解中你还会看到更多文理科共享的知识点,甚至考题的形式都是一摸一样的!
好,我们还是回到这道题目本身:如果我是一个酷爱炫技的无良老师,其实大可以对这个题目冠以「秒杀技巧」的名头,但我并不想让你「秒杀」题目,我想向你解释一点更比秒杀更本质的东西——
我猜你会有疑问:「射影定理」这个知识点根本不在高考大纲上,阅卷组为什么还认为它不算超纲呢?超纲不超纲,这事儿到底是怎么定的?
是的,「射影定理」未被纳入《高考大纲》的正式文本描述,但是!注意下面这句话:
「射影定理」是「余弦定理」的一个直接来源
「射影定理」是「余弦定理」的一个直接来源
「射影定理」是「余弦定理」的一个直接来源(重要的内容说三遍)
——而后者则是《高考大纲》的明确考点:
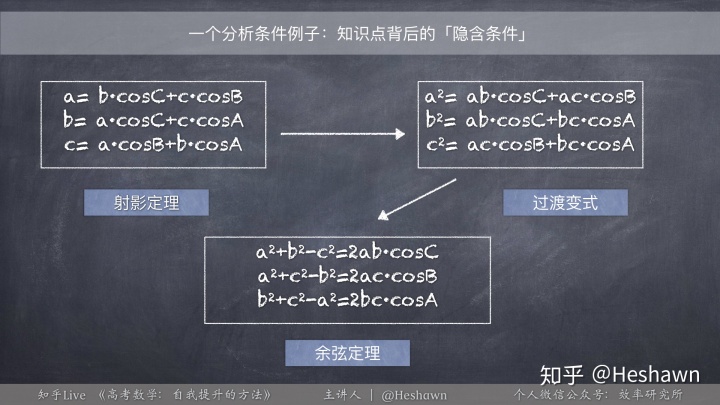
上面这张PPT至少体现了两点内容:
1、首先,射影定理是余弦定理的一个「来源」;
2、进一步地、请你仔细观察:上面的三个部分之间没有引入任何新的信息,仅仅通过「射影定理」之间的公式变换,我们就能得出「余弦定理」——换言之:射影定理和余弦定理是同一个规律的两种不同表述形式。
因为「余弦定理」是考纲重点,而「射影定理」又和「余弦定理」等价、甚至比「余弦定理」更本质——因为他甚至是考点的直接来源——所以这就不算超纲内容。
而我在《有哪些高中不会讲,但解题时非常好用的知识?- Heshawn的回答》这篇文章中特别说过:
如果想要寻找「非常好用的知识」,你不应该顺着知识点往后推,而应该顺着知识点往源头挖—— 知识点往后推论,得到的只能是不计其数的细枝末节,但如果你能理解知识点的「来源」,你就能得到更本质的理解。
好了,我们最后来总结一下这篇文章的重点:
1、文、理科数学大部分知识点、甚至相关知识点的考查形式都是共同的,甚至往年理科题目过几年就会出现在文科试卷上,反之亦然,所以刷题时不应该有特别的偏见;
2、「射影定理」和「余弦定理」其实是同一条定理在不同角度下的观察结果;
3、想找「解题时好用的知识点」,你不应该顺着知识点往后推,而应该沿着知识点的来源往前找。
希望这篇文章能够对你有所帮助,也欢迎你把它 点赞 & 收藏,方便自己随时回顾。
- 关于高中备考,你一定还想看: