牛的旅行

ssl 1119

luogu 1522

题目大意

有两堆点，每一堆点之中的任何两个点都一定有相连的路线，连接两堆点中的各一个点，使最远的两个点的距离最短

---

原题

农民John的农场里有很多牧区。有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言，你能看到至少有两个牧区不连通。这样，农民John就有多个牧区了。

John想在农场里添加一条路径(注意，恰好一条)。对这条路径有以下限制：

一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。考虑如下的有5个牧区的牧场，牧区用星号表示，路径用直线表示。每一个牧区都有自己的坐标：

这个牧场的直径大约是12.07106,最远的两个牧区是A和E，它们之间的最短路径是A-B-E。

这里是另一个牧场：

这两个牧场都在John的农场上。John将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。

注意，如果两条路径中途相交，我们不认为它们是连通的。只有两条路径在同一个牧区相交，我们才认为它们是连通的。

输入文件包括牧区、它们各自的坐标，还有一个如下的对称邻接矩阵：

A B C D E F G H

A 0 1 0 0 0 0 0 0

B 1 0 1 1 1 0 0 0

C 0 1 0 0 1 0 0 0

D 0 1 0 0 1 0 0 0

E 0 1 1 1 0 0 0 0

F 0 0 0 0 0 0 1 0

G 0 0 0 0 0 1 0 1

H 0 0 0 0 0 0 1 0

输入文件至少包括两个不连通的牧区。

请编程找出一条连接两个不同牧场的路径，使得连上这条路径后，这个更大的新牧场有最小的直径。

Input

第1行: 一个整数N (1 <= N <= 150), 表示牧区数

第2到N+1行: 每行两个整数X,Y (0 <= X ,Y<= 100000), 表示N个牧区的坐标。注意每个 牧区的坐标都是不一样的。

第N+2行到第2*N+1行: 每行包括N个数字(0或1) 表示如上文描述的对称邻接矩阵。

Output

只有一行，包括一个实数，表示所求答案。数字保留六位小数。

Sample Input

8

10 10

15 10

20 10

15 15

20 15

30 15

25 10

30 10

01000000

10111000

01001000

01001000

01110000

00000010

00000101

00000010

Sample Output

22.071068

解题方法：

先求出两个区块的最短路，再求出每个区块中每个点与相距此点最大的点的距离，枚举两边的所有点，将任意两个点（不同区域）连接后的的结果就是两个点的距离加上两个点在本区域的相差最大的距离(若不懂，看代码)

注意：

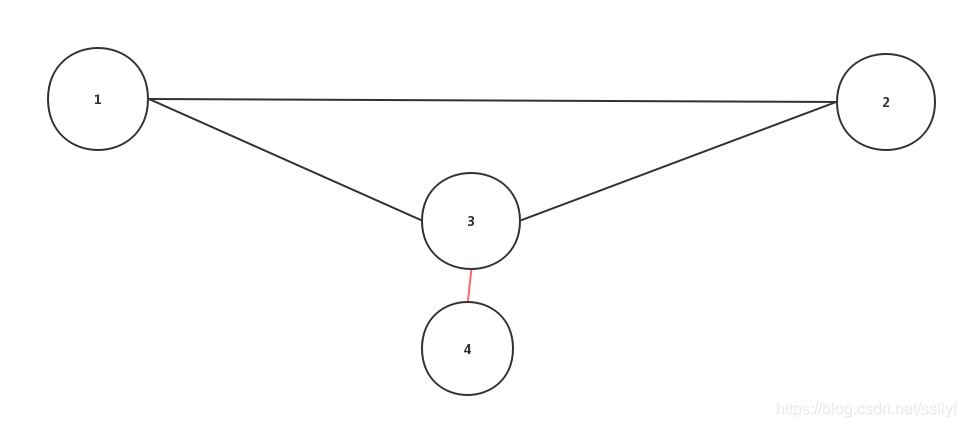
当出现下图时(推荐按住左键再移动来放大图片)，要连接3和4，但最大长度不是1-3-4或2-3-4，而是1-2，所以要注意

#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<string>
using namespace std;
int n;
double f[152][152],b[152],jl[152][152],ans,g,sum;
char t;
struct rec
{int x,y;
}a[152];
int main()
{scanf("%d",&n);for (int i=1;i<=n;i++)scanf("%d %d",&a[i].x,&a[i].y);memset(f,0x7f,sizeof(f));//初值memset(jl,0x7f,sizeof(jl));g=f[0][0];//记录最大值for (int i=1;i<=n;i++){getchar();//换行for (int j=1;j<=n;j++){t=getchar();//输入jl[i][j]=sqrt(double((a[i].x-a[j].x)*(a[i].x-a[j].x))+double((a[i].y-a[j].y)*(a[i].y-a[j].y)));//用勾股定理求距离if (t=='1') f[i][j]=jl[i][j];//f用来求最短路}}for (int k=1;k<=n;k++)for (int i=1;i<=n;i++)for (int j=1;j<=n;j++)if ((i!=j)&&(j!=k)&&(k!=i)&&(f[i][k]+f[k][j]<f[i][j]))f[i][j]=min(f[i][k]+f[k][j],f[i][j]);//求最短路for (int i=1;i<=n;i++){for (int j=1;j<=n;j++)if (f[i][j]!=g)b[i]=max(f[i][j],b[i]);//求距离最长的sum=max(sum,b[i]);//记录}ans=g;for (int i=1;i<=n;i++)for (int j=1;j<=n;j++)if ((f[i][j]==g)&&(i!=j))//要不同区ans=min(ans,b[i]+b[j]+jl[i][j]);//连接printf("%.6lf",max(ans,sum));//输出最大的return 0;
}

温馨提示：

在luogu中要用scanf("%s")来一行一行地输入字符数组