如果你使用过 WPF/UWP 等 XAML UI 框架，那么应该了解到附加属性的概念。那么没有依赖属性支持的时候如何做附加属性的功能呢？你可能会想到弱引用。但这需要做一个弱引用字典，要写的代码还是非常麻烦的。

本文介绍 .NET 的 ConditionalWeakTable<TKey,TValue> 类型，适用于 .NET Framework 4.0 以上和全部 .NET Core 的版本。

---

这不是字典

现成可用的弱引用字典，即 ConditionalWeakTable<TKey,TValue>。然而实际上这个类的原本作用并不是当作字典使用！

如果你使用过 WPF/UWP 等 XAML UI 框架，那么应该了解到附加属性的概念。这其实是 .NET 为我们提供的一种附加字段的机制。

比如你有一个类：

class Foo
{
    // 请忽略这里公有字段带来的设计问题，只是为了演示。
    public string A;
}

我们希望为它增加一个字段 Bar：

class Foo
{
    public string A;
    public Bar Bar;
}

那么我们需要修改类 Foo 本身以实现这个效果；但是这样就使得 Foo 耦合了 Bar，从而破坏了内聚性/依赖倒置原则。典型的情况是 Foo 类表示一个人 Person，它里面不应该包含一个 某行账号 这样的字段，因为很多人是没有那家银行账号的。这个信息让那家银行存起来才是比较符合设计原则的设计。

我们可以通过一个字典 Dictionary<Foo, Bar> 来存储所有 Foo 实例额外增加的 Bar 的值可以避免让 Foo 类中增加 Bar 字段从而获得更好的设计。但这样就引入了一个静态字典从而使得所有的 Foo 和 Bar 的实例无法得到释放。我们想当然希望拥有一个弱引用字典来解决问题。然而这是一个 X-Y 问题。

实际上 .NET 中提供了 ConditionalWeakTable<TKey,TValue> 帮我们解决了最本质的问题——在部分场景下期望为 Foo 类添加一个字段。虽然它不是弱引用字典，但能解决此类问题，同时也能当作一个弱引用字典来使用，仅此而已。

你需要注意的是，ConditionalWeakTable<TKey,TValue> 并不实现 IDictionary<TKey,TValue> 接口，只是里面有一些像 IDictionary<TKey, TValue> 的方法，可以当作字典使用，也可以遍历取出剩下的所有值。

验证

ConditionalWeakTable<TKey,TValue> 中的所有 Key 和所有的 Value 都是弱引用的，并且会在其 Key 被回收或者 Key 和 Value 都被回收之后自动从集合中消失。这意味着当你使用它来为一个类型附加一些字段或者属性的时候完全不用担心内存泄漏的问题。

下面我写了一段代码用于验证其内存泄漏问题：

1. 向 ConditionalWeakTable<TKey,TValue> 中添加了三个键值对；

2. 将后两个的 key 设为 null；

3. 进行垃圾回收。

using System;
using System.Linq;
using System.Runtime.CompilerServices;

namespace Walterlv.Demo.Weak
{
    class Program
    {
        public static void Main()
        {
            var key1 = new Key("Key1");
            var key2 = new Key("Key2");
            var key3 = new Key("Key3");

            var table = new ConditionalWeakTable<Key, WalterlvValue>
            {
                {key1, new WalterlvValue()},
                {key2, new WalterlvValue()},
                {key3, new WalterlvValue()}
            };

            var weak2 = new WeakReference(key2);
            key2 = null;
            key3 = null;

            GC.Collect();

            Console.WriteLine($@"key1 = {key1?.ToString() ?? "null"}key2 = {key2?.ToString() ?? "null"}, weak2 = {weak2.Target ?? "null"}key3 = {key3?.ToString() ?? "null"}Table = {{{string.Join(", ", table.Select(x => $"{x.Key} = {x.Value}"))}}}");
        }
    }

    public class Key
    {
        private readonly string _name;
        public Key(string name) => _name = name;
        public override string ToString() => _name;
    }

    public class WalterlvValue
    {
        public DateTime CreationTime = DateTime.Now;
        public override string ToString() => CreationTime.ToShortTimeString();
    }
}

这段代码的运行结果如下图：

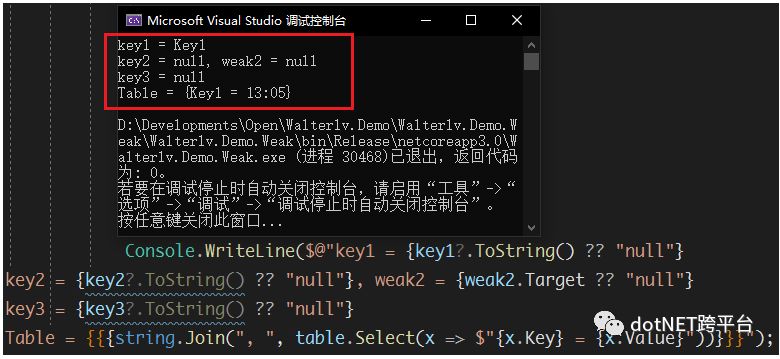
从中我们可以发现：

1. 当某个 Key 被回收后，ConditionalWeakTable<TKey,TValue> 中就没有那一项键值对了；

2. 当 Key 的实例依然在的时候，ConditionalWeakTable<TKey,TValue> 中的 Value 依然还会存在。

另外，我们这里在调查内存泄漏问题，你需要在 Release 配置下执行此代码才能得到最符合预期的结果。

---

参考资料

• ConditionalWeakTable<TKey,TValue> Class (System.Runtime.CompilerServices) - Microsoft Docs

• Good implementation of weak dictionary in .Net - Stack Overflow

• Presenting WeakDictionary[TKey, TValue] – Nick Guerrera’s blog

• .net - Understanding ConditionalWeakTable - Stack Overflow

原文地址：https://blog.walterlv.com/post/conditional-weak-table.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com