小智最近迷上了计算机算法，今天过来给大家讲讲排序算法。
准备讲排序算法之前，我们还是要先回顾一下排序这个概念。
排序是一门古老的科学。排序问题，用数学的方式可以表达如下
问题输入：给定n个数，a1, a2, a3, ..., an
要求输出：给出n个数的排列，a1', a2', a3', ..., an'，使得 a1' ≤ a2' ≤ a3' ≤ ... ≤ an'。
从更形象的角度来说，排序就是一群人站成一列，高的站前面，矮的站在后面。
一个家庭的所有成员按身高排列的示意图（小智实在找不到图了，画一个示意-_-）
关于排序，有几个描述算法特征的词语：
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
时间复杂度：一个算法执行所耗费的时间。
空间复杂度：运行完一个程序所需内存的大小。
ok，了解完排序的相关概念以后，我有一个新的问题了：如何评价一个算法？小智认为，可以用一个词语来形容一个优秀的算法：多快好省。
什么是“多快好省”？我们从算法的角度来解析一下：
多：能够可靠处理大规模的数据
快：算法的时间复杂度要更低的
好：算法实现要符合稳定性
省：算法的空间复杂度要更低的
到底哪些算法能够符合“多快好省”这个目标呢？我们先看一下目前的算法分类：
基于比较的排序算法的特征总结
注：本文不讨论非基于比较算法，比如计数排序、桶排序和基数排序
“多”的角度：从数据量的处理性能来看，需要不受随机因素影响的算法。冒泡算法、插入排序、快速排序这三个算法最好情况和最坏情况相差了一个数量级，这种不可靠性可能影响数据处理的效率。
“快”的角度：从时间复杂度的角度来看，希尔排序、归并排序、快速排序、堆排序的算法复杂度比较好，均低于O(n2)。
“好”的角度：从稳定性的角度来看，归并排序、插入排序、冒泡排序是稳定的
“省”的角度：从空间复杂度的角度来看，冒泡排序、插入排序、希尔排序、堆排序，空间复杂度为O(1)。其中，值得注意的是，一般写法的归并排序，空间复杂度为O(n)，经过优化以后，使用空间可以为O(1)。
大家都看出了我的倾向了吧？小智从“多快好省”这四个方面，分析发现，归并算法在这四个方面表现不错。这次小智决定跟大家探讨一下归并算法。
为什么归并排序能够做到多快好省？
解答这个问题之前，我们先了解一下什么是归并排序。
归并算法（merge sort）是一个分治算法（divide and conquer algorithm），冯·诺依曼（John von Neumann ）在1945年发明了这个算法。这个算法将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有序。
实际上，归并算法的算法步骤非常简单：
第1步：拆分，把长度为n的输入序列分成两个长度为n/2的子序列
第2步：递归调用，对这两个子序列分别使用归并排序
第3步：合并，将两个排序好的子序列合并成一个最终的排序序列
这几步，我们来分别地讲一下：
什么是拆分？将一个长序列拆分成两个子序列。这个属于分治法中的“分”，将大问题降解为小问题。
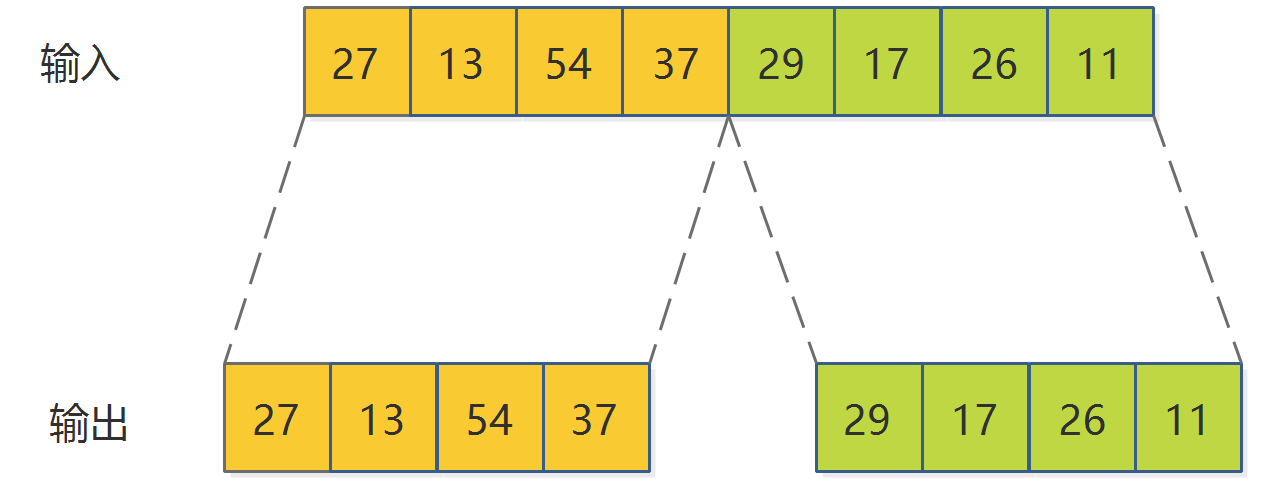
将长序列拆分成两个子序列示意图
如果n为奇数，不能被2整除，可以将n/2向上取整，这个对算法没有影响。
有一个特殊情况是需要注意的：当子序列长度为1时，已经没有办法进行拆分了，可以直接执行下一步。
什么是递归调用？实际上是重复调用归并排序的程序。我们假想一下，在最开始的情况下，执行完第1步，长序列被拆分为2个子序列。接着执行第二步时，直接对子序列进行归并排序，那么下一步则是继续拆分子序列。如此下去，直至将长序列拆分到无法分拆的情形。
我们以图来说明会更加清晰一点：
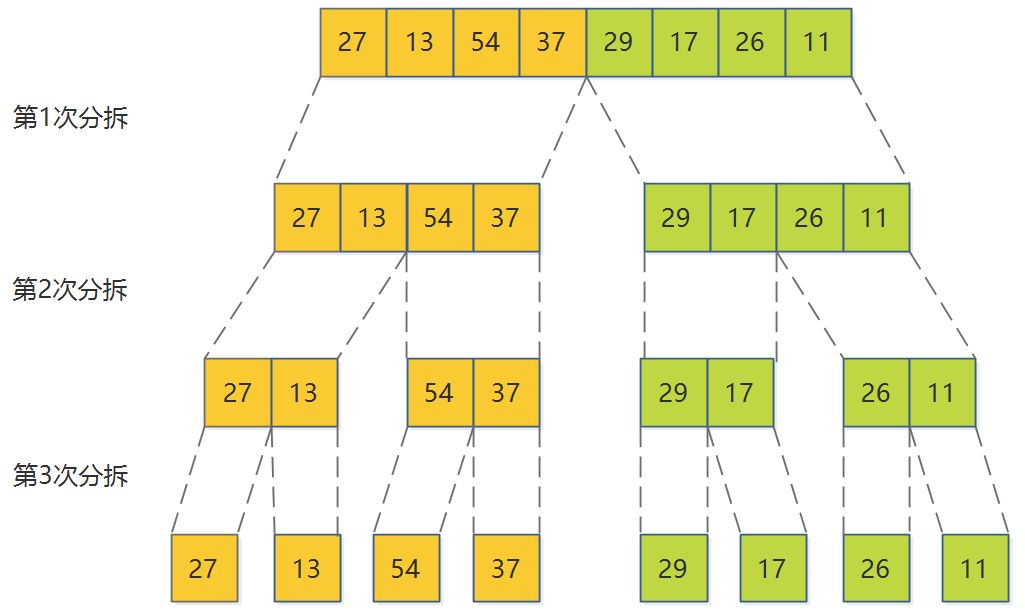
归并算法递归调用的分拆效果
经过不断地递归调用，要处理的子序列长度越来越短，最后直至子序列长度为1。
有一个特殊情况是需要注意的：当子序列长度为1时，已经不需要继续调用归并排序了，因此可以直接跳过递归调用这个步骤。
什么是合并？是将两个排好序的子序列，合成一个也是排好序的序列。这个合并算法也是比较简单。
合并过程可以表述为：对于两个子序列，X和Y，其中X和Y都是升序排列，以及知道X和Y每个数据在原来长序列的位置，分别为Xp和Yp，如何将X和Y合并成一个稳定的升序排列？
由于这两个子序列都是升序排列，因此我们同时遍历这两个子序列，从遍历的位置各拿出一个数字，哪个数字小就把它拿出来插入合并序列中。如果遇到拿出来的两个数字相等的情况，则比较原来序列的位置，哪个小就把它拿出来即可。
按照上述合并步骤，我们可以写出合并伪代码了：
i = 1, j = 1, l = 1
申请一个临时变量temp，用于储存合并后序列
如果 X[i] < Y[j]: temp[l] = X[i], l = l + 1, i = i + 1
如果 X[i] < Y[j]: temp[l] = Y[j], l = l + 1, j = j + 1
如果 X[i] = Y[j]:
如果 Xp[i] < Yp[j]: temp[l] = X[i], l = l + 1, i = i + 1
如果 Xp[i] > Yp[j]: temp[l] = Y[j], l = l + 1, j = j + 1
我将合并流程补充到整个归并算法的执行流程当中，以图的形式做了一个示例：
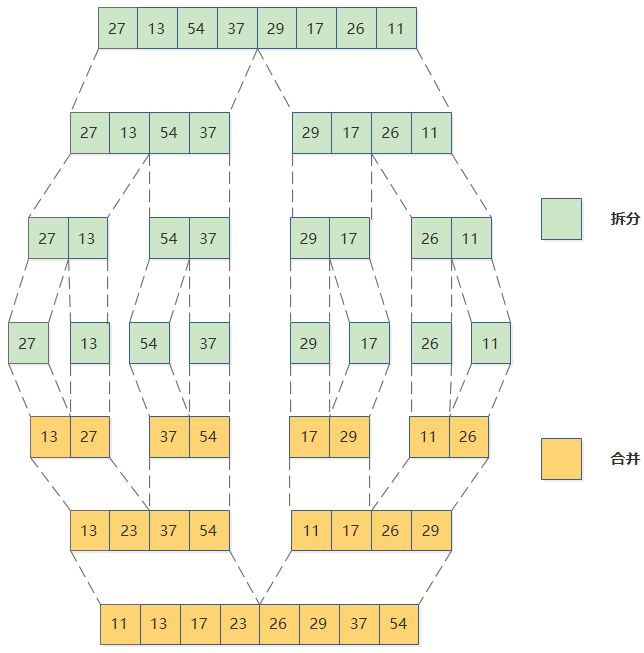
归并排序整体流程示意图
归并排序我们了解完了，我们可以开始回答为什么归并排序能够表现如此出色：
“多”的角度：归并排序为什么能保证可靠地处理数据？
归并排序的拆分的流程，跟数据的原始排序没有关系，无论是最坏情况还是最好情况，时间复杂度都是一致的，能够稳定处理大量数据。
“快”的角度：归并排序的时间复杂度为什么是 O(n log n)?
设归并排序所消耗的时间为T(n)，进行归并排序的拆分操作以后，将原来的问题划分为原来规模的二分之一，每一个划分出来的问题将耗费时间是T(n/2)，最后把这两部分有序的数组合并在一起所花的时间为O(n)，因此：
T(n) = 2×T(n/2) + O(n)
而划分次数最多可以有log2 n次，因此累加起来可得T(n) = O(n log n)
“好”的角度：归并排序为什么能保证稳定呢？
归并排序将序列分割到最小，而后将序列进行合并。假如两个数字是相等的，在分割子序列的时候，不会更改他们之间的相对位置；在合并子序列的时候，只要能够做到先将位置在前的数字放到合并数组，这样就保证了排序结果的稳定。
“省”的角度：归并排序为什么空间复杂度可以为O(1)？
归并排序虽然原始写法的确是这样的，但是算法是可以改造的，我们只需要做到原地排序就可以了，而对于归并排序而言，原地排序的关键是合并。归并排序的原来写法，当进行合并时，是申请一个临时空间，将合并的数据放到临时空间当中，这个算法复杂度为 O(n) 。
实际上，合并过程可以直接使用已有的位置。假设我们要合并的两段数组还是[13, 23, 37, 54]和[11,17, 26,29]，在归并算法里，它们可以看成一个连续的数组形式：
[13, 23, 37, 54, 11, 17, 26, 29]
首先我们检查两段数组的第一个数，发现13 > 11，那么11这个数要拿出来，原来是要放到临时空间的第一个位置，但我们可以利用数组已有的位置，将11直接移到数组的第一个位置，然后原来第一段数组往后移一个位置，这样数组变为
[11, 13, 23, 37, 54, 17, 26, 29]
而后我们继续按照这种方式，合并[13, 23. 37. 54]和[17, 26 29]这两段数组。
可以发现，这种方式空间复杂度只需一个临时变量，用于协助数字移动，因此空间复杂度为O(1)。当然这样优化增加了移动的次数，为了空间，就要损失时间了。
总结一下，归并排序是个宝，一个多快好省的排序算法，大家如果遇到数据排序问题，可以优先考虑它。当然，归并排序并不是全能的，在某些类型问题下，有些算法比归并排序表现更为出色，往后小智会给大家解读。
 php,js-eval编码,js-eval解码)
