参考引用：A Story of Basis and Kernel 来源：http://songcy.net/

向量与内积

在一个

空间中，我们可以通过

个独立向量的线性组合来表示这个空间里的任意向量。这些独立的向量可以看作是空间里的一组基，基向量互相正交。比如

就是一组正交基向量（

的第

个元素为

，其余元素为

）。

内积运算可以衡量两个向量的相似度

如果

以及

，那么这两个向量的内积为

向量向函数的拓展

一个函数可以看作是无限维向量。

一个定义在区间

的函数

，我们可以以

为间隔对函数进行采样，从而将函数（由函数在不同点的取值组成）转化为一个向量

，当采样间隔趋于零时，这一向量就会无限趋近于函数

（或者说可以用向量来表征函数）且此时向量的维度是无穷维的。

既然函数可以理解是一种特殊的向量，那么同样可以近似定义函数的内积

因为向量的维度都是离散整数，而函数的维度是连续的，用了normalization这里采用

表示相邻维度的差。

在向量空间中，我们可以用一组基向量来表示任意向量，函数空间也可以用一组基函数来表征其他函数。但是向量空间的基向量是有限的，函数空间的基函数可能是无限的。函数空间的基函数也是要求互相正交的，两个函数的内积如果是零则表示两个函数是正交的。

例子：Fourier Series

假设基函数为

，

为整数，且

定义在区间

。这些函数构造了一个函数空间，且任意定义在

上的函数可以表示为这些基函数的线性组合。可以证明任意两个基函数是正交的

其中

，基函数的长度为

。

如果一个函数定义在此空间的区间

上，则可以表示为

，对应某一个点

的函数值为

因为

所以这些系数可以计算得到

也就是傅里叶级数。

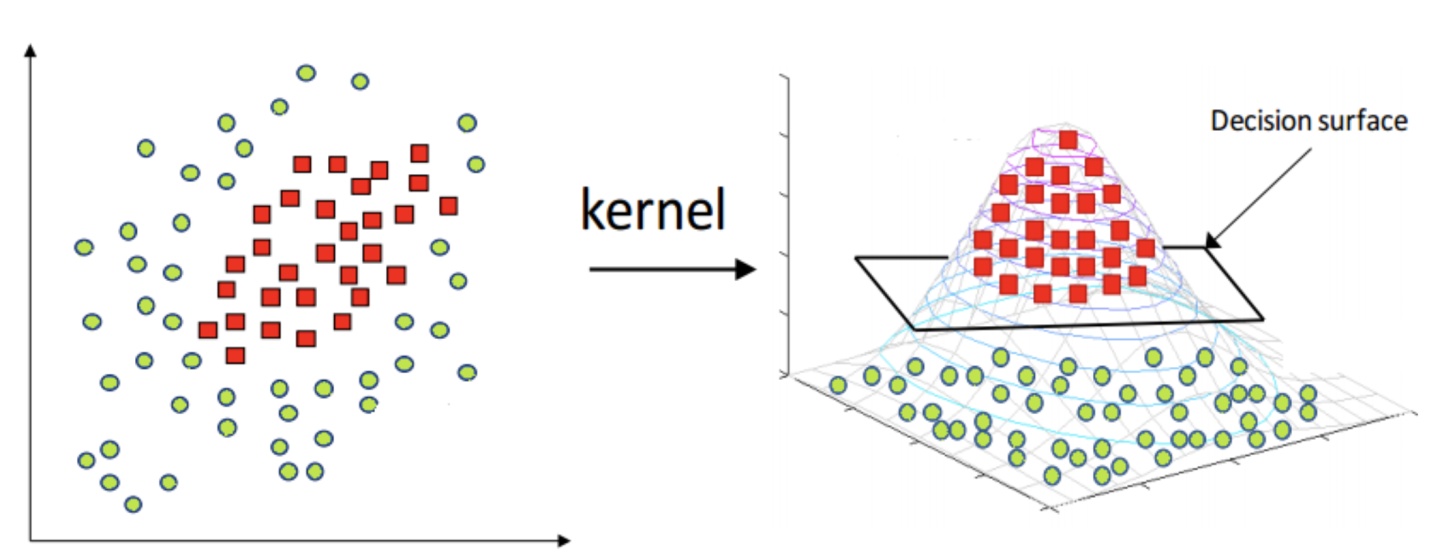
核方法

核方法的目的在于将一个

上的向量映射到另外一个特征空间上，比如一个更高维的空间。此时

特征分解

考虑一个实对称矩阵

，存在实数

以及向量

使得

则称

是矩阵

的一个特征值，

是对应的特征向量。如果

有两个不同的特征值

以及对应的特征向量

，那么可以证明

，即两个特征向量是正交的。

更一般的，对于矩阵

，我们可以找到

个特征值以及

个正交的特征向量。使得矩阵可以分解为

其中

为正交矩阵（

），

。如果我们将

按列向量展开描述

，则

其中

为

空间的一组正交基。

核函数

因为函数

可以看作是一个无限维的向量，那么对于一个二元函数

，我们可以将其看做是一个无限维矩阵。如果这个函数满足

且

对于任意函数

均成立。

则

是对称正定的，在这种情况下它是一个核函数。

类比于矩阵的特征分解，存在特征值

以及特征函数

使得

对于不同的特征值

以及对应的特征函数

有

因此有基函数的内积为零

，即基函数是正交的。

对于一个核函数（无穷维矩阵），有无限多的特征值

以及对应的基函数

，类似于矩阵我们可以得到

对应核函数（无穷维矩阵）的某个元素有

这也就是Mercer定理。这里

。

再生核希尔伯特空间

将

看作是构成希尔伯特空间

的一组正交基，那么任意在这个空间的一个点（函数）可以表示为这组基的线性组合。

表示一个函数，

表示函数在

的取值。

，即

对于任意函数，我们可以将其看作是一个无限维向量（函数在每一个输入

的取值），这个函数的向量表示为

。这么一个无穷维向量对应到空间的基表示为

（

。

此时核函数的一行

（固定

）可以表示为

上式可以对照矩阵分解来理解，矩阵中的某一行对应

的其中一行，所以第一个向量应该只取一个元素；回到这里也就是核函数的某一行对应的是

而不是

。

对应的是一个无穷维向量

那么根据内积的定义有

可以理解为内积转化为无穷维向量对应元素相乘，再转化为系数乘以基构成一个函数后再取某一个元素

，也就是函数在

的取值。

同样可以推导（无穷维向量的对应元素相乘）

这就是再生性质，因此

称为再生核希尔伯特空间。

如果我们定义

为从

映射到希尔伯特空间后的无穷维向量，则

也就是人们常说的通过核函数，我们可以将一个向量映射到再生核希尔伯特空间中的一个无穷维向量（函数）。

进一步有

即两个无穷维向量的内积等于核函数在点

的取值。因此我们并不需要知道这个映射是什么，这个特征空间在哪里，这个特征空间的基函数是什么。就可以求得无穷维空间上的内积。

这也被称作核技巧。